紅黑樹的性質：
性質1：每個節點要么是黑色，要么是紅色。
- 性質2：根節點是黑色。
- 性質3：每個葉子節點（NIL）是黑色。
- 性質4：每個紅色節點的兩個子節點一定都是黑色。不能有兩個紅色節點相連。
- 性質5：任意一節點到每個葉子節點的路徑都包含數量相同的黑結點。俗稱：黑高！
- 從性質5又可以推出：性質5.1：如果一個節點存在黑子節點，那么該結點肯定有兩個子節點
總結：
根節點必黑，新增是紅色，只能黑連黑，不能紅連紅
紅黑樹的操作：
紅黑樹能自平衡，它靠的三種操作：左旋、右旋和變色。
1.變色：結點的顏色由紅變黑或由黑變紅。
2.左旋：以某個結點作為支點(旋轉結點)，其右子結點變為旋轉結點的父結點，右子結點的左子結點變為旋轉結點的右子結點，左子結點保持不變。
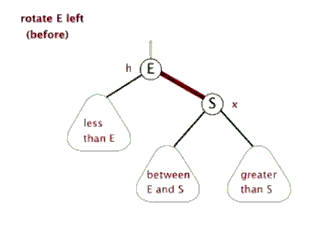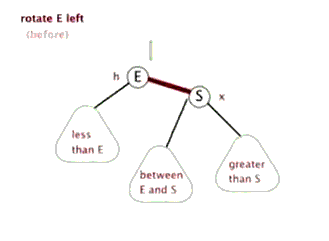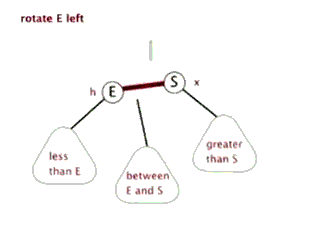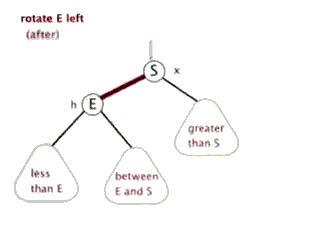
3.右旋：以某個結點作為支點(旋轉結點)，其左子結點變為旋轉結點的父結點，左子結點的右子結點變為旋轉結點的左子結點，右子結點保持不變
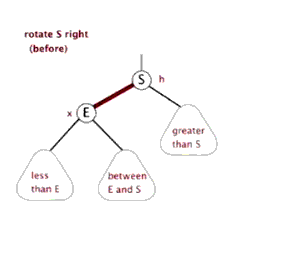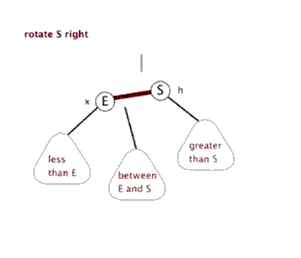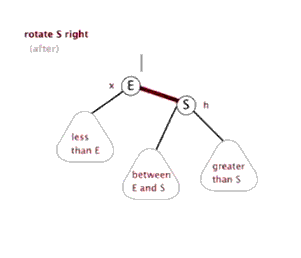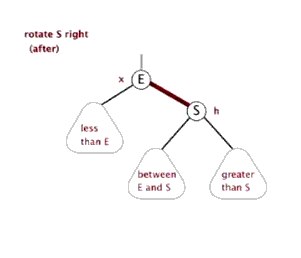
紅黑樹插入節點情景分析
情景1：紅黑樹為空樹
最簡單的一種情景，直接把插入結點作為根結點就行
注意：根據紅黑樹性質2：根節點是黑色。還需要把插入結點設為黑色。
情景2：插入結點的Key已存在
處理：更新當前節點的值，為插入節點的值
情景3：插入結點的父結點為黑結點
由于插入的結點是紅色的，當插入結點的黑色時，并不會影響紅黑樹的平衡，直接插入即可，無需做自平衡。
情景4：插入節點的父節點為紅色
再次回想下紅黑樹的性質2：根結點是黑色。如果插入節點的父結點為紅結點，那么該父結點不可能為根結點，所以插入結點總是存在祖父結點。
這一點很關鍵，因為后續的旋轉操作肯定需要祖父結點的參與
插入情景4.1：叔叔結點存在并且為紅結點
依據紅黑樹性質4可知，紅色節點不能相連 ==> 祖父結點肯定為黑結點；
因為不可以同時存在兩個相連的紅結點。那么此時該插入子樹的紅黑層數的情況是：黑紅紅。顯然最簡單的處理方式是把其改為：紅黑紅
處理：
1.將P和U節點改為黑色
2.將PP改為紅色
3.將PP設置為當前節點，進行后續處理
插入情景4.2：叔叔結點不存在或為黑結點，并且插入結點的父親結點是祖父結點的左子結點
注意：單純從插入前來看，叔叔節點非紅即空（NIL節點），否則的話破壞了紅黑樹性質5，此路徑會比其它路徑多一個黑色節點。
插入情景4.2.1：新插入節點，為其父節點的左子節點（LL紅色情況）
處理：
1.變顏色：將P設置為黑色，將PP設置為紅色
2.對PP節點進行右旋
插入情景4.2.2：新插入節點，為其父節點的右子節點（LR紅色情況）
處理：
1.對P進行左旋
2.將P設置為當前節點，得到LL紅色情況
3.按照LL紅色情況處理（1.變顏色 2.右旋PP）
插入情景4.3：叔叔結點不存在或為黑結點，并且插入結點的父親結點是祖父結點的右子結點
處理：
1.變顏色：將P設置為黑色，將PP設置為紅色
2.對PP節點進行左旋
插入情景4.3.2：新插入節點，為其父節點的左子節點（RL紅色情況）
處理：
1.對P進行右旋
2.將P設置為當前節點，得到RR紅色情況
3.按照RR紅色情況處理（1.變顏色 2.左旋PP）
總結
爸叔通紅就變色，爸紅叔黑就旋轉，哪邊黑往哪邊轉。
