Machine learning and deep learning models are data-hungry. The performance of them is highly dependent on the amount of data. Thus, we tend to collect as much data as possible in order to build a robust and accurate model. Data is collected in many different formats from numbers to images, from text to sound waves. However, we need to convert the data to numbers in order to analyze and model it.

機器學習和深度學習模型需要大量數據。 它們的性能高度依賴于數據量。 因此，我們傾向于收集盡可能多的數據，以建立可靠而準確的模型。 數據以多種不同的格式收集，從數字到圖像，從文本到聲波。 但是，我們需要將數據轉換為數字，以便對其進行分析和建模。

It is not enough just to convert data to scalars (single numbers). As the amount of data increases, the operations done with scalars start to be inefficient. We need vectorized or matrix operations to make computations efficiently. That’s where linear algebra comes into play.

僅將數據轉換為標量(單個數字)是不夠的。 隨著數據量的增加，使用標量執行的操作開始效率低下。 我們需要向量化或矩陣運算來有效地進行計算。 那就是線性代數起作用的地方。

Linear algebra is one of the most important topics in data science domain. In this post, we will cover the basic concepts in linear algebra with examples using NumPy.

線性代數是數據科學領域中最重要的主題之一。 在本文中，我們將使用NumPy的示例介紹線性代數的基本概念。

NumPy is a scientific computing library for Python and forms the basis of many libraries such as Pandas.

NumPy是用于Python的科學計算庫，它構成了許多庫(例如Pandas)的基礎。

線性代數中的對象類型 (Types of Objects in Linear Algebra)

Types of objects (or data structures) in linear algebra:

線性代數中的對象(或數據結構)類型：

• Scalar: Single number
  標量：單個數字
• Vector: Array of numbers
  向量：數字數組
• Matrix: 2-dimensional array of numbers
  矩陣：二維數字數組
• Tensor: N-dimensional array of numbers where n > 2
  張量：N維數數組，其中n> 2

A scalar is just a number. It can be used in vectorized operations as we will see in the following examples.

標量只是一個數字。 如下面的示例所示，它可以用于矢量化操作。

A vector is an array of numbers. For instance, following is a vector with 5 elements:

向量是數字數組。 例如，下面是一個包含5個元素的向量：

We can use scalars in vectorized operations. The specified operation is done on each element of the vector and scalar.

我們可以在向量化運算中使用標量。 對向量和標量的每個元素執行指定的操作。

A matrix is a 2-dimensional vector.

矩陣是二維向量。

It seems like a pandas dataframe with rows and columns. Actually, pandas dataframes are converted to matrices and then fed into machine learning models.

好像是一個帶有行和列的熊貓數據框。 實際上，熊貓數據幀會轉換為矩陣，然后輸入到機器學習模型中。

A tensor is an N-dimensional array of numbers where N is greater than 2. Tensors are mostly used in deep learning models where the input data is 3-dimensional.

張量是數字的N維數組，其中N大于2。張量通常用于輸入數據為3維的深度學習模型中。

It is hard easy to represent with numbers but think of T as 3 matrices with a shape of 3x2.

很難用數字表示，但是將T視為3x2形狀的3個矩陣。

The shape method can be used to check the shape of a numpy array.

shape方法可用于檢查numpy數組的形狀 。

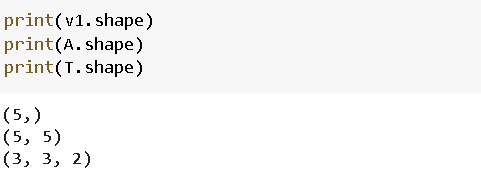
The size of an array is calculated by multiplying the size in each dimension.

數組的大小是通過將每個維度的大小相乘得出的。

通用矩陣術語 (Common Matrix Terms)

A matrix is called square if number of rows is equal to the number of columns. thus, the matrix A above is a square matrix.

如果行數等于列數，則矩陣稱為正方形 。 因此，上面的矩陣A是正方形矩陣。

Identity matrix, denoted as I, is a square matrix that have 1’s on the diagonal and 0’s at all other positions. Identity function of NumPy can be used create identity matrices of any size.

單位矩陣，表示為I，是一個對角線為1且在所有其他位置為0的方陣。 NumPy的身份函數可用于創建任何大小的身份矩陣。

What makes an identity matrix special is that it does not change a matrix when multiplied. In this sense, it is similar to number 1 in real numbers. We will do examples with identity matrix in matrix multiplication part of this post.

使單位矩陣與眾不同的原因是，乘法時它不會改變矩陣。 從這個意義上講，它與實數上的數字1相似。 我們將在本文的矩陣乘法部分中以恒等矩陣為例。

The inverse of a matrix is the matrix that gives the identity matrix when multiplied with the original matrix.

矩陣的逆矩陣是與原始矩陣相乘時給出單位矩陣的矩陣。

Not every matrix has an inverse. If matrix A has an inverse, then it is called invertible or non-singular.

并非每個矩陣都有逆。 如果矩陣A具有逆，則稱其為可逆 或非奇異。

點積和矩陣乘法 (Dot Product and Matrix Multiplication)

Dot product and matrix multiplication are the building blocks of complex machine learning and deep learning models so it is highly valuable to have a comprehensive understanding of them.

點積和矩陣乘法是復雜的機器學習和深度學習模型的基礎，因此全面了解它們非常有價值。

The dot product of two vectors is the sum of the products of elements with regards to their position. The first element of the first vector is multiplied by the first element of the second vector and so on. The sum of these products is the dot product. The function to compute dot product in NumPy is dot().

兩個向量的點積是元素相對于其位置的乘積之和。 第一個向量的第一個元素乘以第二個向量的第一個元素，依此類推。 這些乘積之和為點積。 在NumPy中計算點積的函數是dot() 。

Let’s first create two simple vectors in the form of numpy arrays and calculate the dot product.

首先，我們以numpy數組的形式創建兩個簡單的向量，然后計算點積。

The dot product is calculated as (1*2)+(2*4)+(3*6) which is 28.

點積計算為(1 * 2)+(2 * 4)+(3 * 6)，即28。

Since we multiply elements at the same positions, the two vectors must have same length in order to have a dot product.

由于我們在相同位置上乘以元素，因此兩個向量必須具有相同的長度才能具有點積。

In the field of data science, we mostly deal with matrices. A matrix is a bunch of row and column vectors combined in a structured way. Thus, multiplication of two matrices involves many dot product operations of vectors. It will be more clear when we go over some examples. Let’s first create two 2x2 matrices with NumPy.

在數據科學領域，我們主要處理矩陣。 矩陣是以結構化方式組合的一堆行和列向量。 因此， 兩個矩陣的乘法涉及向量的許多點積運算 。 當我們回顧一些示例時，將更加清楚。 我們首先使用NumPy創建兩個2x2矩陣。

A 2x2 matrix has 2 rows and 2 columns. Index of rows and columns start with 0. For instance, the first row of A (row with index 0) is the array of [4,2]. The first column of A is the array of [4,0]. The element at first row and first column is 4.

2x2矩陣有2行2列。 行和列的索引以0開頭。例如，A的第一行(索引為0的行)是[4,2]的數組。 A的第一列是[4,0]的數組。 第一行和第一列的元素是4。

We can access individual rows, columns, or elements as follows:

我們可以按以下方式訪問單獨的行，列或元素：

These are important concepts to comprehend matrix multiplication.

這些是理解矩陣乘法的重要概念。

Multiplication of two matrices involves dot products between rows of first matrix and columns of the second matrix. The first step is the dot product between the first row of A and the first column of B. The result of this dot product is the element of resulting matrix at position [0,0] (i.e. first row, first column).

兩個矩陣的乘法涉及第一矩陣的行和第二矩陣的列之間的點積。 第一步是A的第一行和B的第一列之間的點積。該點積的結果是位置[0,0](即第一行，第一列)處所得矩陣的元素。

So the resulting matrix, C, will have a (4*4) + (2*1) at the first row and first column. C[0,0] = 18.

因此，所得矩陣C在第一行和第一列將具有(4 * 4)+(2 * 1)。 C [0,0] = 18

The next step is the dot product of the first row of A and the second column of B.

下一步是A的第一行和B的第二列的點積。

C will have a (4*0) + (2*4) at the first row and second column. C[0,1] = 8.

C在第一行和第二列將具有(4 * 0)+(2 * 4)。 C [0,1] = 8

First row A is complete so we start on the second row of A and follow the same steps.

第一行A已完成，因此我們從A的第二行開始并遵循相同的步驟。

C will have a (0*4) + (3*1) at the second row and first column. C[1,0] = 3.

C在第二行和第一列將具有(0 * 4)+(3 * 1)。 C [1,0] = 3。

The final step is the dot product between the second row of A and the second column of B.

最后一步是A的第二行和B的第二列之間的點積。

C will have a (0*0) + (3*4) at the second row and second column. C[1,1] = 12.

C在第二行和第二列將具有(0 * 0)+(3 * 4)。 C [1,1] = 12

We have seen how it is done step-by-step. All of these operations are done with a np.dot operation:

我們已經看到了它是如何逐步完成的。 所有這些操作都是通過np.dot操作完成的：

As you may recall, we have mentioned that identity matrix does not change a matrix when multiplied. Let’s do an example.

您可能還記得，我們已經提到了單位矩陣在相乘時不會改變。 讓我們做一個例子。

We have also mentioned that when a matrix is multiplied by its inverse, the result is the identity matrix. Let’s first create a matrix and find its inverse. We can use linalg.inv() function of NumPy to find the inverse of a matrix.

我們還提到過，當矩陣乘以其逆矩陣時，結果就是單位矩陣。 首先創建一個矩陣并找到其逆矩陣。 我們可以使用NumPy的linalg.inv()函數來查找矩陣的逆。

Let’s multiply B with its inverse matrix, C :

讓我們將B與其逆矩陣C相乘：

Bingo! We have the identity matrix.

答對了！ 我們有單位矩陣。

As we recall from vector dot products, two vectors must have the same length in order to have a dot product. Each dot product operation in matrix multiplication must follow this rule. Dot products are done between the rows of the first matrix and the columns of the second matrix. Thus, the rows of the first matrix and columns of the second matrix must have the same length.

正如我們從向量點積中回憶起的那樣， 兩個向量必須具有相同的長度才能具有點積 。 矩陣乘法中的每個點積運算必須遵循此規則。 點積在第一矩陣的行和第二矩陣的列之間完成。 因此， 第一矩陣的行和第二矩陣的列必須具有相同的長度。

The requirement for matrix multiplication is that the number of columns of the first matrix must be equal to the number of rows of the second matrix.

矩陣乘法的要求是，第一個矩陣的列數必須等于第二個矩陣的行數。

For instance, we can multiply a 3x2 matrix with a 2x3 matrix.

例如，我們可以將3x2矩陣與2x3矩陣相乘。

The shape of the resulting matrix will be 3x3 because we are doing 3 dot product operations for each row of A and A has 3 rows. An easy way to determine the shape of the resulting matrix is to take the number of rows from the first one and the number of columns from the second one:

最終矩陣的形狀將為3x3，因為我們對A的每一行進行了3個點積運算，而A具有3行。 確定結果矩陣形狀的一種簡單方法是從第一個矩陣中獲取行數，從第二個矩陣中獲取列數：

• 3x2 and 2x3 multiplication returns 3x3
  3x2和2x3乘法返回3x3
• 3x2 and 2x2 multiplication returns 3x2
  3x2和2x2乘法返回3x2
• 2x4 and 4x3 multiplication returns 2x3
  2x4和4x3乘法返回2x3

We have covered basic but very fundamental operations of linear algebra. These basic operations are the building blocks of complex machine learning and deep learning models. Lots of matrix multiplication operations are done during the optimization process of models. Thus, it is highly important to understand the basics as well.

我們已經介紹了線性代數的基本但非常基本的運算。 這些基本操作是復雜的機器學習和深度學習模型的基礎。 在模型優化過程中完成了許多矩陣乘法運算。 因此，了解基礎知識也非常重要。

Thank you for reading. Please let me know if you have any feedback.

感謝您的閱讀。 如果您有任何反饋意見，請告訴我。