一、數學建模概述

監督學習:通過已有的訓練樣本進行訓練得到一個最優模型,再利用這個模型將所有的輸入映射為相應的輸出。監督學習根據輸出數據又分為回歸問題(regression)和分類問題(classfication),回歸問題的輸出通常是連續的數值,分類問題的輸出通常是幾個特定的數值。
非監督學習:根據類別未知的訓練樣本,解決模式識別中的各種問題,主要為聚類問題(cluster analysis)。
?
二、回歸分析概述?
在統計學中,回歸分析(regression analysis)指的是確定兩種或兩種以上變量間互相依賴的定量關系的一種統計分析方法。
根據自變量和因變量之間的關系類型,可分為線性回歸分析和非線性回歸分析。
?
線性回歸linear analys
線性回歸通常是學習預測模型時首選的技術之一。在線性回歸中,因變量是連續的,而自變量可以是連續的的也可以是離散的,回歸線的性質是線性的。
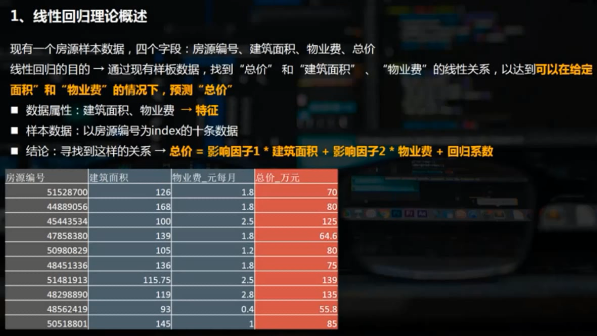
線性回歸使用最佳的擬合直線(即回歸線)在因變量y和一個或多個自變量x之間建立一種關系,簡單線性回歸(一元線性回歸)可表示為y=a+b*x
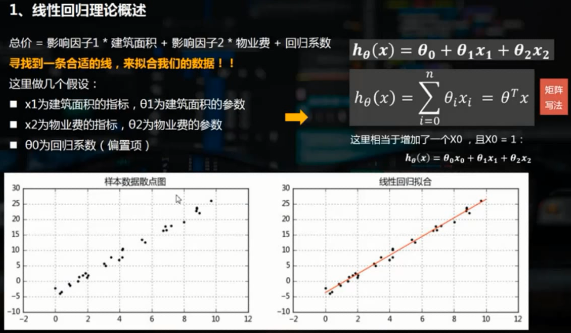
多元線性回歸可表示為y=a+b1*x1+b2*x2。線性回歸可以根據給定的預測變量s來預測目標變量的值。
 ??
?? ??
??
 ??
??
?
三、使用python實現線性回歸分析
需要先安裝sklearn模塊,并導入其中的線性回歸類from sklearn.linear_model import LinearRegression
model = LinearRegression()? 創建模型
model.fit(x,y)? 將樣本導入模型,x需要是列變量
print('斜率和截距分別為:',model.coef_,model.intercept_)
y_pre = model.predict(x_pre)? ?通過模型預測給定的自變量對應的因變量
?
1.一元線性回歸
rng = np.random.RandomState(1) #生成隨機數種子,種子相同每次生成的隨機數相同 x = 10 * rng.rand(30) #通過隨機數種子生成隨機數 y = 8 + 4 * x + rng.rand(30) # rng.rand(30)表示誤差 #生成隨機數x和y,擬合樣本關系y = 8 + 4*x fig = plt.figure(figsize=(10,4)) ax1 = fig.add_subplot(121) plt.scatter(x,y,s = 10) plt.title('樣本散點圖')model = LinearRegression() # 創建線性回歸模型 model.fit(x[:,np.newaxis],y) # 給模型導入樣本值,第一個參數為自變量,第二個參數為因變量,x[:,np.newaxis]表示給x在列上增加一個維度,不能直接使用x print('斜率為%f,截距為%f'%(model.coef_,model.intercept_)) # 斜率為4.004484,截距為8.447659 xtest = np.linspace(0,10,1000) ytest = model.predict(xtest[:,np.newaxis]) # 通過模型預測自變量對應的因變量 ax1 = fig.add_subplot(122) plt.scatter(x,y,s = 10) plt.plot(xtest,ytest,color = 'red') #擬合線性回歸直線 plt.title('線性回歸擬合圖')
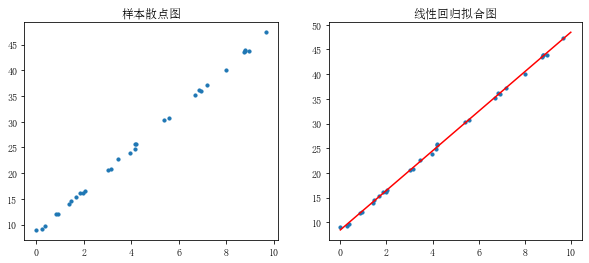
?
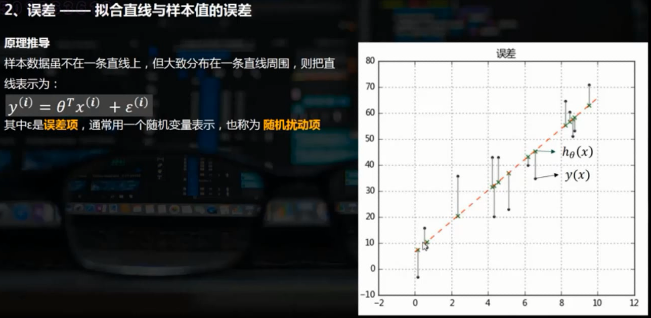
誤差,即樣本實際值與擬合得到的樣本值的差
rng = np.random.RandomState(2) x = 10 * rng.rand(20) y = 8 + 4 * x + rng.rand(20)*30 #誤差乘以20是為了在圖表中明顯顯示 model = LinearRegression() model.fit(x[:,np.newaxis],y) xtest = np.linspace(0,10,1000) ytest = model.predict(xtest[:,np.newaxis])plt.plot(xtest,ytest,color = 'r',alpha = 0.7) # 擬合線性回歸直線 plt.scatter(x,y,s = 10,color='green') # 樣本散點圖 y2 = model.predict(x[:,np.newaxis]) # 樣本x在擬合直線上的y值 plt.scatter(x,y2,marker = '+',color = 'k') # 樣本x擬合y的散點圖 plt.plot([x,x],[y,y2],color = 'gray') #誤差線 plt.title('誤差線')
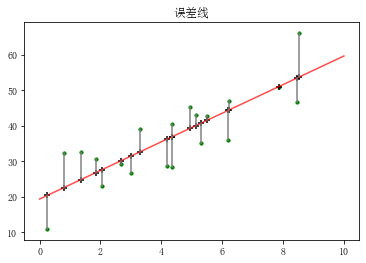
?
?2.多元線性回歸
矩陣點積參考https://blog.csdn.net/skywalker1996/article/details/82462499
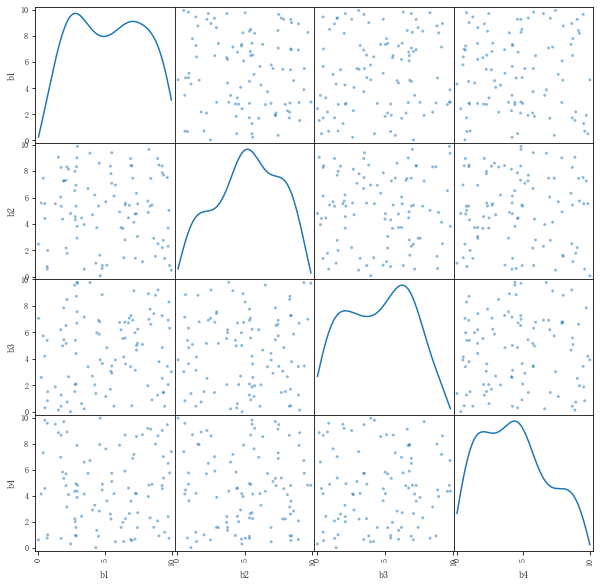
rng = np.random.RandomState(3) x = 10 * rng.rand(100,4) y = 20 + np.dot(x,[1.5,2,-4,3]) + rng.rand(100) df = pd.DataFrame(x,columns=['b1','b2','b3','b4']) df['y'] = y df.head() pd.plotting.scatter_matrix(df[['b1','b2','b3','b4']],figsize = (10,10),diagonal='kde') #根據矩陣散點圖判斷4個變量之間相互獨立,不需降維 model = LinearRegression() model.fit(df[['b1','b2','b3','b4']],df['y']) print('斜率為:',model.coef_,type(model.coef_)) print('截距為:',model.intercept_) print('線性回歸函數為y = %.1fx1 + %.1fx2 + %.1fx3 + %.1fx4 + %.1f'%(model.coef_[0],model.coef_[1],model.coef_[2],model.coef_[3],model.intercept_)) # 斜率為: [ 1.50321961 2.0000257 -3.99067203 2.99358669] <class 'numpy.ndarray'> # 截距為: 20.489657423197222 # 線性回歸函數為y = 1.5x1 + 2.0x2 + -4.0x3 + 3.0x4 + 20.5
四、線性回歸模型評估
通過幾個參數驗證回歸模型
- SSE:和方差、誤差平方和,the sum of squares due to error
- MSE:均方差、方差,mean squared error
- RMSE:均方根、標準差,root mean squared error
- R-square:確定系數,coefficient of determination
1.SSE(和方差)
該統計參數計算的是擬合數據和原始數據對應點的誤差的平方和,計算公式如下。
SSE越接近于0,說明模型選擇和擬合更好,數據預測也越成功。接下來的MSE和RMSE因為和SSE同出一宗,效果一樣。
2.MSE(均方差)
該統計參數是預測數據和原始數據對應點誤差的平方和的均值,也就是SSE/n,和SSE沒有太大的區別,計算公式如下。
3.RMSE(均方根)
該統計參數也叫回歸系統的擬合標準差,是MSE的平方根,就算公式如下
在這之前,誤差參數都是基于預測值和原始值之間的誤差(即點對點),而下面的誤差是相對原始數據平均值而展開的(即點對全)。
4.R-square(確定系數)
①SSR:Sum of squares of the regression,即預測數據與原始數據均值之差的平方和,公式如下。
②SST:Total sum of squares,即原始數據和均值之差的平方和,公式如下。
細心的網友會發現,SST=SSE+SSR,而“確定系數”是定義為SSR和SST的比值,故
其實“確定系數”是通過數據的變化來表征一個擬合的好壞。由上面的表達式可以知道“確定系數”的正常取值范圍為[0,1],越接近1表明方程的變量對y的解釋能力越強,這個模型對數據擬合的也較好。
from sklearn import metricsrng = np.random.RandomState(6) x = 10 * rng.rand(30) y = 8 + 4 * x + rng.rand(30) * 3model = LinearRegression() model.fit(x[:,np.newaxis],y) # 回歸擬合 ytest = model.predict(x[:,np.newaxis]) # 求出預測數據 sse = ((ytest - y)**2).sum() # 求SSE,也可通過該方法得到SSE,再除以len(x)得到MSE mse = metrics.mean_squared_error(ytest,y) # 求均方差MSE,也可通過該方法算出MSE,再乘以len(x)得到SSE rmse = np.sqrt(mse) # 求均方根RMSE# ssr = ((ytest - y.mean())**2).sum() # 求預測數據與原始數據均值之差的平方和 # sst = ((y - y.mean())**2).sum() # 求原始數據和原始數據均值之差的平方和 # rr = ssr / sst # 求確定系數 r = model.score(x[:,np.newaxis],y) # 求出確定系數print('和方差SSE為:%.5f'%sse) print('均方差MSE為: %.5f'% mse) print('均方根RMSE為: %.5f'% rmse) print('確定系數R-square為: %.5f'% r) # 和方差SSE為:16.54050 # 均方差MSE為: 0.55135 # 均方根RMSE為: 0.74253 # 確定系數R-square為: 0.99512
?
5.線性回歸模型評估總結
主要是用MSE和 R_square。
如果是對一個樣本做兩個回歸模型,可以分別判斷哪個MSE更小哪個就更好、哪個R接近于1哪個就更好。如果只有一個回歸模型,判斷R是否接近1,大于0.6、0.8就非常不錯了。同時在后續做組成成分分析,假如有10個參數,做一個回歸模型后做一個R模型評估,比如說R為0.85,把這10個參數降維為3個主成分,再做一個3元的線性回歸,R為0.92,則3元線性回歸模型的R為0.92更好,相互比較做出最優比較。
?
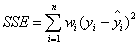
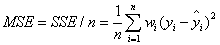
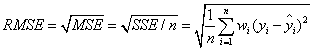
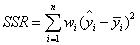
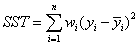
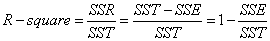
)





)
:函數與函數式編程)



)


)
![bzoj千題計劃169:bzoj2463: [中山市選2009]誰能贏呢?](http://pic.xiahunao.cn/bzoj千題計劃169:bzoj2463: [中山市選2009]誰能贏呢?)



