接近組數據(組間) (Approaching group data (between-group))

A typical situation regarding solving an experimental question using a data-driven approach involves several groups that differ in (hopefully) one, sometimes more variables.

使用數據驅動的方法解決實驗性問題的典型情況涉及幾個組(希望)不同，有時甚至更多。

Say you collect data on people that either ate (Group 1) or did not eat chocolate (Group 2). Because you know the literature very well, and you are an expert in your field, you believe that people that ate chocolate are more likely to ride camels than people that did not eat the chocolate.

假設您收集的是吃過(第1組)或沒有吃巧克力(第2組)的人的數據。 因為您非常了解文獻，并且您是該領域的專家，所以您認為吃巧克力的人比沒有吃巧克力的人騎駱駝的可能性更高。

You now want to prove that empirically.

您現在想憑經驗證明這一點。

I will be generating simulation data using Python, to demonstrate how permutation testing can be a great tool to detect within group variations that could reveal peculiar patterns of some individuals. If your two groups are statistically different, then you might explore what underlying parameters could account for this difference. If your two groups are not different, you might want to explore whether some data points still behave “weirdly”, to decide whether to keep on collecting data or dropping the topic.

我將使用Python生成仿真數據，以演示置換測試如何成為檢測組內變異的好工具，這些變異可以揭示某些個體的特殊模式。 如果兩組在統計上不同，那么您可能會探索哪些基礎參數可以解釋這一差異。 如果兩組沒有不同，則可能要探索某些數據點是否仍然表現“怪異”，以決定是繼續收集數據還是刪除主題。

# Load standard libraries
import panda as pd 
import numpy as np
import matplotlib.pyplot as plt

Now one typical approach in this (a bit crazy) experimental situation would be to look at the difference in camel riding propensity in each group. You could compute the proportions of camel riding actions, or the time spent on a camel, or any other dependent variable that might capture the effect you believe to be true.

現在，在這種(有點瘋狂)實驗情況下，一種典型的方法是查看每組中騎駱駝傾向的差異。 您可以計算騎駱駝動作的比例，騎駱駝的時間或其他任何可能捕捉到您認為是真實的效果的因變量。

產生資料 (Generating data)

Let’s generate the distribution of the chocolate group:

讓我們生成巧克力組的分布：

# Set seed for replicability
np.random.seed(42)# Set Mean, SD and sample size
mean = 10; sd=1; sample_size=1000# Generate distribution according to parameters
chocolate_distibution = np.random.normal(loc=mean, scale=sd, s
size=sample_size)# Show data
plt.hist(chocolate_distibution)
plt.ylabel("Time spent on a camel")
plt.title("Chocolate Group")

As you can see, I created a distribution centered around 10mn. Now let’s create the second distribution, which could be the control, centered at 9mn.

如您所見，我創建了一個以1000萬為中心的發行版。 現在，讓我們創建第二個分布，該分布可能是控件，以900萬為中心。

mean = 9; sd=1; sample_size=1000
non_chocolate_distibution = np.random.normal(loc=mean, scale=sd, size=sample_size)
fig = plt.figure()
plt.hist(non_chocolate_distibution)
plt.ylabel("Time spent on a camel")
plt.title("Non Chocolate Group")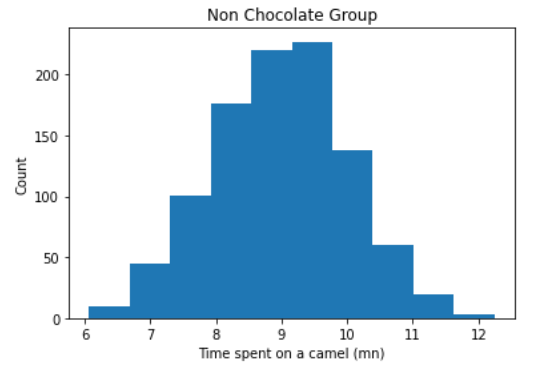

OK! So now we have our two simulated distributions, and we made sure that they differed in their mean. With the sample size we used, we can be quite sure we would have two significantly different populations here, but let’s make sure of that. Let’s quickly visualize that:

好！ 因此，現在我們有了兩個模擬分布，并確保它們的均值不同。 使用我們使用的樣本量，我們可以確定這里會有兩個明顯不同的總體，但是讓我們確定一下。 讓我們快速想象一下：

We can use an independent sample t-test to get an idea of how different these distributions might be. Note that since the distributions are normally distributed (you can test that with a Shapiro or KS test), and the sample size is very high, parametric testing (under which t-test falls) is permitted. We should run a Levene’s test as well to check the homogeneity of variances, but for the sake of argumentation, let’s move on.

我們可以使用獨立的樣本t檢驗來了解這些分布可能有多大差異。 請注意，由于分布是正態分布的(可以使用Shapiro或KS檢驗進行測試)，并且樣本量非常大，因此可以進行參數檢驗(t檢驗屬于這種檢驗)。 我們也應該運行Levene檢驗來檢驗方差的均勻性，但是為了論證，讓我們繼續。

from scipy import stats
t, p = stats.ttest_ind(a=chocolate_distibution, b=non_chocolate_distibution, axis=0, equal_var=True)
print('t-value = ' + str(t))
print('p-value = ' + str(p))

Good, that worked as expected. Note that given the sample size, you are able to detect even very small effects, such as this one (distributions’ means differ only by 1mn).

很好，按預期工作。 請注意，在給定樣本量的情況下，您甚至可以檢測到很小的影響，例如這種影響(分布的均值相差僅100萬)。

If these would be real distributions, one would have some evidence that chocolate affects the time spent riding a camel (and should of course dig down a bit more to see what could explain that strange effect…).

如果這些是真實的分布，則將有一些證據表明巧克力會影響騎駱駝的時間(當然，應該多挖一點，看看有什么能解釋這種奇怪的作用……)。

I should note that at some point tough, this kind of statistics become dangerous because of the high sample size, that outputs extremely high p-values for even low effects. I discuss a bit this issue in this post. Anyway, this post is about approaching individual data, so let’s move on.

我應該指出，由于樣本量太大，這種統計數據有時會變得很危險，因為即使樣本量很小，其輸出的p值也非常高。 我在這篇文章中討論了這個問題。 無論如何，這篇文章是關于處理單個數據的，所以讓我們繼續。

處理單個數據(組內) (Approaching individual data (within-group))

Now let’s assume that for each of these participants, you recorded multiple choices (Yes or No) to ride a camel (you probably want to do this a few times per participants to get reliable data). Thus, you have repeated measures, at different time points. You know that your groups are significantly different, but what about `within group` variance? And what about an alternative scenario where your groups don’t differ, but you know some individuals showed very particular behavior? The method of permutation can be used in both cases, but let’s use the scenario generated above where groups are significanly different.

現在，假設對于每個參與者，您記錄了騎駱駝的多個選擇(是或否)(您可能希望每個參與者進行幾次此操作以獲得可靠的數據)。 因此，您將在不同的時間點重復進行測量。 您知道您的小組有很大不同，但是“小組內”差異又如何呢？ 在您的小組沒有不同但您知道某些人表現出非常特殊的行為的情況下，又該如何呢？ 兩種情況下都可以使用置換方法，但是讓我們使用上面生成的方案，其中組明顯不同。

What you might observe is that, while at the group level you do have a increased tendency to ride camels after your manipulation (eg, giving sweet sweet chocolate to your subjects), within the chocolate group, some people have a very high tendency while others are actually no different than the No Chocolate group. Vice versa, maybe within the non chocolate group, while the majority did not show an increase in the variable, some did (but that effect is diluted by the group’s tendency).

您可能會觀察到的是，雖然在小組級別上，您在操縱后確實騎駱駝的趨勢有所增加(例如，給受試者提供甜甜的巧克力)，但是在巧克力小組中 ，有些人的趨勢非常高，而其他人實際上與“無巧克力”組沒有什么不同。 反之亦然，也許在非巧克力組中，雖然大多數沒有顯示變量的增加，但有一些確實存在(但這種影響因該組的趨勢而被淡化)。

One way to test that would be to use a permutation test, to test each participants against its own choice patterns.

一種測試方法是使用置換測試，以針對每個參與者自己的選擇模式進行測試。

資料背景 (Data background)

Since we are talking about choices, we are looking at a binomial distribution, where say 1 = Decision to ride a camel and 0 = Decision not to ride a camel.Let’s generate such a distribution for a given participant that would make 100 decisions:

既然我們在談論選擇，我們正在看一個二項式分布，其中說1 =騎駱駝的決定和0 = 不騎駱駝的決定，讓我們為給定的參與者生成這樣的分布，它將做出100個決定：

Below, one example where I generate the data for one person, and bias it so that I get a higher number of ones than zeros (that would be the kind of behavior expected by a participant in the chocolate group

在下面的示例中，我為一個人生成數據，并對數據進行偏倚，這樣我得到的數據要多于零(這是巧克力組參與者期望的行為)

distr = np.random.binomial(1, 0.7, size=100)
print(distr)

# Plot the cumulative data
pd.Series(distr).plot(kind=’hist’)

We can clearly see that we have more ones than zeros, as wished.

我們可以清楚地看到，正如我們所希望的那樣，我們的數字多于零。

Let’s generate such choice patterns for different participants in each group.

讓我們為每個組中的不同參與者生成這種選擇模式。

為所有參與者生成選擇數據 (Generating choice data for all participants)

Let’s say that each group will be composed of 20 participants that made 100 choices.

假設每個小組將由20個參與者組成，他們做出了100個選擇。

In an experimental setting, we should probably have measured the initial preference of each participant to like camel riding (maybe some people, for some reason, like it more than others, and that should be corrected for). That measure can be used as baseline, to account for initial differences in camel riding for each participant (that, if not measured, could explain differences later on).

在實驗環境中，我們可能應該已經測量了每個參與者對騎駱駝的喜好(也許某些人由于某種原因比其他人更喜歡駱駝，應該對此進行糾正)。 該度量可以用作基準，以說明每個參與者騎駱駝的初始差異(如果不進行度量，則可以稍后解釋差異)。

We thus will generate a baseline phase (before giving them chocolate) and an experimental phase (after giving them chocolate in the chocolate group, and say another neutral substance in the non chocolate group (as a control manipulation).

因此，我們將生成一個基線階段(在給他們巧克力之前)和一個實驗階段(在給他們巧克力組中的巧克力之后，并說非巧克力組中的另一種中性物質(作為對照操作)。

A few points:1) I will generate biased distributions that follow the pattern found before, i.e., that people that ate chocolate are more likely to ride a camel.2) I will produce baseline choice levels similar between the two groups, to make the between group comparison statistically valid. That is important and should be checked before you run more tests, since your groups should be as comparable as possible.3) I will include in each of these groups a few participants that behave according to the pattern in the other group, so that we can use a permutation method to detect these guys.

有幾點要點： 1)我將按照以前發現的模式生成有偏差的分布，即吃巧克力的人騎駱駝的可能性更大。 2)我將產生兩組之間相似的基線選擇水平，以使組之間的比較在統計上有效。 這很重要，應該在運行更多測試之前進行檢查，因為您的組應盡可能具有可比性。 3)我將在每個小組中包括一些參與者，這些參與者根據另一小組中的模式進行舉止，以便我們可以使用排列方法來檢測這些家伙。

Below, the function I wrote to generate this simulation data.

下面是我編寫的用于生成此模擬數據的函數。

def generate_simulation_data(nParticipants, nChoicesBase,             nChoicesExp, binomial_ratio):    """
    Generates a simulation choice distribution based on parameters
    Function uses a binomial distribution as basis
    params: (int) nParticipants, number of participants for which   we need data    params: (int) nChoicesBase, number of choices made in the baseline period    params: (int) nChoicesExp, number of choices made in the experimental period    params: (list) binomial_ratio, ratio of 1&0 in the resulting binomial distribution. Best is to propose a list of several values of obtain variability.
    """    # Pre Allocate
    group = pd.DataFrame()    # Loop over participants. For each draw a binonimal choice distribution    for i in range (0,nParticipants):        # Compute choices to ride a camel before drinking, same for both groups (0.5) 
        choices_before = np.random.binomial(1, 0.4, size=nChoicesBase)         # Compute choices to ride a camel after drinking, different per group (defined by binomial ratio)        # generate distribution
        choices_after  = np.random.binomial(1, np.random.choice(binomial_ratio,replace=True), size=nChoicesExp)        # Concatenate
        choices = np.concatenate([choices_before, choices_after])        # Store in dataframe
        group.loc[:,i] = choices
    return group.T

Let’s generate choice data for the chocolate group, with the parameters we defined earlier. I use binomial ratios starting at 0.5 to create a few indifferent individuals within this group. I also use ratios > 0.5 since this group should still contain individuals with high preference levels.

讓我們使用前面定義的參數生成巧克力組的選擇數據。 我使用從0.5開始的二項式比率在該組中創建了一些無關緊要的人。 我也使用比率> 0.5，因為該組仍應包含具有較高優先級的個人。

chocolate_grp = generate_simulation_data(nParticipants=20,              nChoicesBase=20, nChoicesExp=100, binomial_ratio=[0.5,0.6,0.7,0.8,0.9])

As we can see, we generated binary choice data for 120 participants. The screenshot shows part of these choices for some participants (row index).

如我們所見，我們為120名參與者生成了二元選擇數據。 屏幕截圖顯示了一些參與者的部分選擇(行索引)。

We can now quickly plot the summed choices for riding a camel for each of these participants to verify that indeed, we have a few indifferent ones (data points around 50), but most of them have a preference, more or less pronounced, to ride a camel.

現在，我們可以為每個參與者快速繪制騎駱駝的總和選擇，以驗證確實有一些冷漠的人(數據點大約為50)，但是其中大多數人或多或少都傾向于騎車一頭駱駝。

def plot_group_hist(data, title):
    data.sum(axis=1).plot(kind='hist')
    plt.ylabel("Number of participants")
    plt.xlabel("Repeated choices to ride a camel")
    plt.title(title)plot_group_hist(chocolate_grp, title=' Chocolate group')

Instead of simply summing up the choices to ride a camel, let’s compute a single value per participant that would reflect their preference or aversion to camel ride.

與其簡單地總結騎駱駝的選擇，不如計算每個參與者的單個值，以反映他們對駱駝騎的偏好或反感。

I will be using the following equation, that basically computes a score between [-1;+1], +1 reflecting a complete switch for camel ride preference after drinking, and vice versa. This is equivalent to other normalizations (or standardizations) that you can find in SciKit Learn for instance.

我將使用以下等式，該等式基本上計算出[-1; +1]，+ 1之間的得分，這反映了飲酒后駱駝騎行偏好的完全轉換，反之亦然。 例如，這等同于您可以在SciKit Learn中找到的其他標準化(或標準化)。

Now, let’s use that equation to compute, for each participant, a score that would inform on the propensity to ride a camel. I use the function depicted below.

現在，讓我們使用該方程式為每個參與者計算一個分數，該分數將說明騎駱駝的傾向。 我使用下面描述的功能。

def indiv_score(data):    """
    Calculate a normalized score for each participant
    Baseline phase is taken for the first 20 decisions
    Trials 21 to 60 are used as actual experimental choices
    """    # Baseline is the first 20 choices, experimental is from choice 21 onwards
    score = ((data.loc[20:60].mean() - data.loc[0:19].mean())
        / (data.loc[20:60].mean() + data.loc[0:19].mean())
        )
    return scoredef compute_indiv_score(data):    """
    Compute score for all individuals in the dataset
    """    # Pre Allocate
    score = pd.DataFrame(columns = ['score'])    # Loop over individuals to calculate score for each one
    for i in range(0,len(data)):        # Calculate score
        curr_score = indiv_score(data.loc[i,:])        # Store score
        score.loc[i,'score'] = curr_score    return scorescore_chocolate = compute_indiv_score(chocolate_grp)
score_chocolate.plot(kind='hist')

We can interpret these scores as suggesting that some individuals showed >50% higher preference to ride a camel after drinking chocolate, while the majority showed an increase in preference of approximately 20/40%. Note how a few individuals, although pertaining to this group, show an almost opposite pattern.

我們可以將這些分數解釋為，表明一些人在喝完巧克力后對騎駱駝的偏好提高了50％以上，而大多數人的偏好提高了約20/40％。 請注意，盡管有些人屬于這個群體，卻表現出幾乎相反的模式。

Now let’s generate and look at data for the control, non chocolate group

現在讓我們生成并查看非巧克力對照組的數據

plot_group_hist(non_chocolate_grp, title='Non chocolate group')\

We can already see that the number of choices to ride a camel are quite low compared to the chocolate group plot.

我們已經可以看到，與巧克力集團相比，騎駱駝的選擇數量非常少。

OK! Now we have our participants. Let’s run a permutation test to detect which participants were significantly preferring riding a camel in each group. Based on the between group statistics, we expect that number to be higher in the chocolate than in the non chocolate group.

好！ 現在我們有我們的參與者。 讓我們運行一個置換測試，以檢測哪些參與者在每個組中明顯更喜歡騎駱駝。 根據小組之間的統計，我們預計巧克力中的這一數字將高于非巧克力組。

排列測試 (Permutation test)

A permutation test consists in shuffling the data, within each participant, to create a new distribution of data that would reflect a virtual, but given the data possible, distribution. That operation is performed many times to generate a virtual distribution against which the actual true data is compared to.

排列測試包括在每個參與者內對數據進行混排，以創建新的數據分布，該分布將反映虛擬但有可能的數據分布。 多次執行該操作以生成虛擬分布，將其與實際的真實數據進行比較。

In our case, we will shuffle the data of each participant between the initial measurement (baseline likelihood to ride a camel) and the post measurement phase (same measure after drinking, in each group).

在我們的案例中，我們將在初始測量(騎駱駝的基準可能性)和測量后階段(每組喝酒后的相同測量)之間對每個參與者的數據進行混洗。

The function below runs a permutation test for all participants in a given group.For each participant, it shuffles the choice data nReps times, and calculate a confidence interval (you can define whether you want it one or two sided) and checks the location of the real choice data related to this CI. When outside of it, the participant is said to have a significant preference for camel riding.

下面的函數對給定組中的所有參與者進行排列測試，對于每個參與者，其洗凈選擇數據nReps次，并計算置信區間(您可以定義是單面還是雙面)并檢查位置與此CI相關的實際選擇數據。 在外面時，據說參與者特別喜歡騎駱駝。

I provide the function to run the permutation below. If is a bit long, but it does the job ;)

我提供了運行以下排列的功能。 如果有點長，但是可以完成工作；)

def run_permutation(data, direct='two-sided', nReps=1000, print_output=False):    """
    Run a permutation test.
    For each permutation, a score is calculated and store in an array.
    Once all permutations are performed for that given participants, the function computes the real score
    It then compares the real score with the confidence interval.
    
    The ouput is a datafram containing all important statistical information.    params: (df) data, dataframe with choice data
    params: (str) direct, default 'two-sided'. Set to 'one-sided' to compute a one sided confidence interval
    params: (int) nReps. number of iterations 
    params: (boolean), default=False. True if feedback to user is needed    """    # PreAllocate significance
    output=pd.DataFrame(columns=['Participant', 'Real_Score', 'Lower_CI', 'Upper_CI', 'Significance'])for iParticipant in range(0,data.shape[0]):        # Pre Allocate
        scores = pd.Series('float')        # Start repetition Loop
        if print_output == True:
            print('Participant #' +str(iParticipant))
        output.loc[iParticipant, 'Participant'] = iParticipant        for iRep in range(0,nReps):
            # Store initial choice distribution to compute real true score
            initial_dat = data.loc[iParticipant,:]            # Create a copy
            curr_dat = initial_dat.copy()            # Shuffle data
            np.random.shuffle(curr_dat)            # Calculate score with shuffled data
            scores[iRep] = indiv_score(curr_dat)
            
        # Sort scores to compute confidence interval
        scores = scores.sort_values().reset_index(drop=True)
        # Calculate confidence interval bounds, based on directed hypothesis
        if direct == 'two-sided':
            upper = scores.iloc[np.ceil(scores.shape[0]*0.95).astype(int)]
            lower = scores.iloc[np.ceil(scores.shape[0]*0.05).astype(int)]
        elif direct == 'one-sided':
            upper = scores.iloc[np.ceil(scores.shape[0]*0.975).astype(int)]
            lower = scores.iloc[np.ceil(scores.shape[0]*0.025).astype(int)]output.loc[iParticipant, 'Lower_CI'] = lower
        output.loc[iParticipant, 'Upper_CI'] = upper        if print_output == True:
            print ('CI = [' +str(np.round(lower,decimals=2)) + ' ; ' + str(np.round(upper,decimals=2)) + ']')
        # Calculate real score
        real_score = indiv_score(initial_dat)
        output.loc[iParticipant, 'Real_Score'] = real_score        if print_output == True:
            print('Real score = ' + str(np.round(real_score,decimals=2)))        # Check whether score is outside CI bound
        if (real_score < upper) & (real_score > lower):
            output.loc[iParticipant, 'Significance'] =0            if print_output == True:
                print('Not Significant')
        elif real_score >= upper:
            output.loc[iParticipant, 'Significance'] =1            if print_output == True:
                print('Significantly above')        else: output.loc[iParticipant, 'Significance']  = -1; print('Significantly below')        if print_output == True:
            print('')
    return output

Now let’s run the permutation test, and look at individual score values

現在讓我們運行置換測試，并查看各個得分值

output_chocolate = run_permutation(chocolate_grp, direct=’two-sided’, nReps=100, print_output=False)
output_chocolate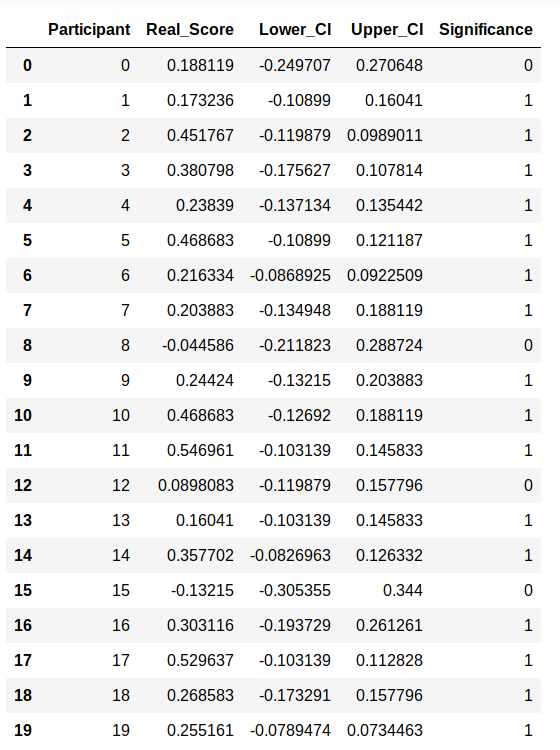

output_non_chocolate = run_permutation(non_chocolate_grp, direct='two-sided', nReps=100, print_output=False)
output_non_chocolate

We can see that, as expected from the way we compute the distributions ,we have much more participants that significantly increased their camel ride preference after the baseline measurement in the chocolate group.

我們可以看到，正如我們從計算分布的方式所預期的那樣，在巧克力組進行基線測量之后，有更多的參與者顯著提高了他們的駱駝騎行偏好。

That is much less likely in the non chocolate group, where we even have one significant decrease in preference (participant #11)

在非巧克力組中，這的可能性要小得多，在該組中，我們的偏好甚至大大降低了(參與者＃11)

We can also see something I find quite important: some participants have a high score but no significant preference, while others have a lower score and a significant preference (see participants 0 & 1 in the chocolate group). That is due to the confidence interval, which is calculated based on each participant’s behavior. Therefore, based on the choice patterns, a given score might fall inside the CI and not be significant, while another, maybe lower score, maybe fall outside this other individual-based CI.

我們還可以看到一些我認為非常重要的東西：一些參與者的得分較高，但沒有明顯的偏好，而另一些參與者的得分較低，并且有明顯的偏好(請參閱巧克力組中的參與者0和1)。 這是由于置信區間是基于每個參與者的行為計算的。 因此，根據選擇模式，給定的得分可能落在CI內，并且不顯著，而另一個得分可能更低，或者落在其他基于個人的CI之外。

最后的話 (Final words)

That was it. Once this analysis is done, you could look at what other, **unrelated** variables, might differ between the two groups and potentially explain part of the variance in the statistics. This is an approach I used in this publication, and it turned out to be quite useful :)I hope that you found this tutorial helpful.Don’t hesitate to contact me if you have any questions or comments!

就是這樣 完成此分析后，您可以查看兩組之間** 無關的 **變量可能不同，并可能解釋統計數據中的部分方差。 這是我在本出版物中使用的一種方法，結果非常有用:)我希望您對本教程有所幫助。如有任何疑問或意見，請隨時與我聯系！

Data and notebooks are in this repo: https://github.com/juls-dotcom/permutation

數據和筆記本在此倉庫中： https : //github.com/juls-dotcom/permutation