城市的天際線是從遠處觀看該城市中所有建筑物形成的輪廓的外部輪廓。給你所有建筑物的位置和高度，請返回由這些建筑物形成的 天際線 。

每個建筑物的幾何信息由數組 buildings 表示，其中三元組 buildings[i] = [lefti, righti, heighti] 表示：

• lefti 是第 i 座建筑物左邊緣的 x 坐標。
• righti 是第 i 座建筑物右邊緣的 x 坐標。
• heighti 是第 i 座建筑物的高度。

天際線 應該表示為由 “關鍵點” 組成的列表，格式 [[x1,y1],[x2,y2],…] ，并按 x 坐標 進行 排序 。關鍵點是水平線段的左端點。列表中最后一個點是最右側建筑物的終點，y 坐標始終為 0 ，僅用于標記天際線的終點。此外，任何兩個相鄰建筑物之間的地面都應被視為天際線輪廓的一部分。

注意：輸出天際線中不得有連續的相同高度的水平線。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正確的答案；三條高度為 5 的線應該在最終輸出中合并為一個：[…[2 3], [4 5], [12 7], …]

• 示例 1：

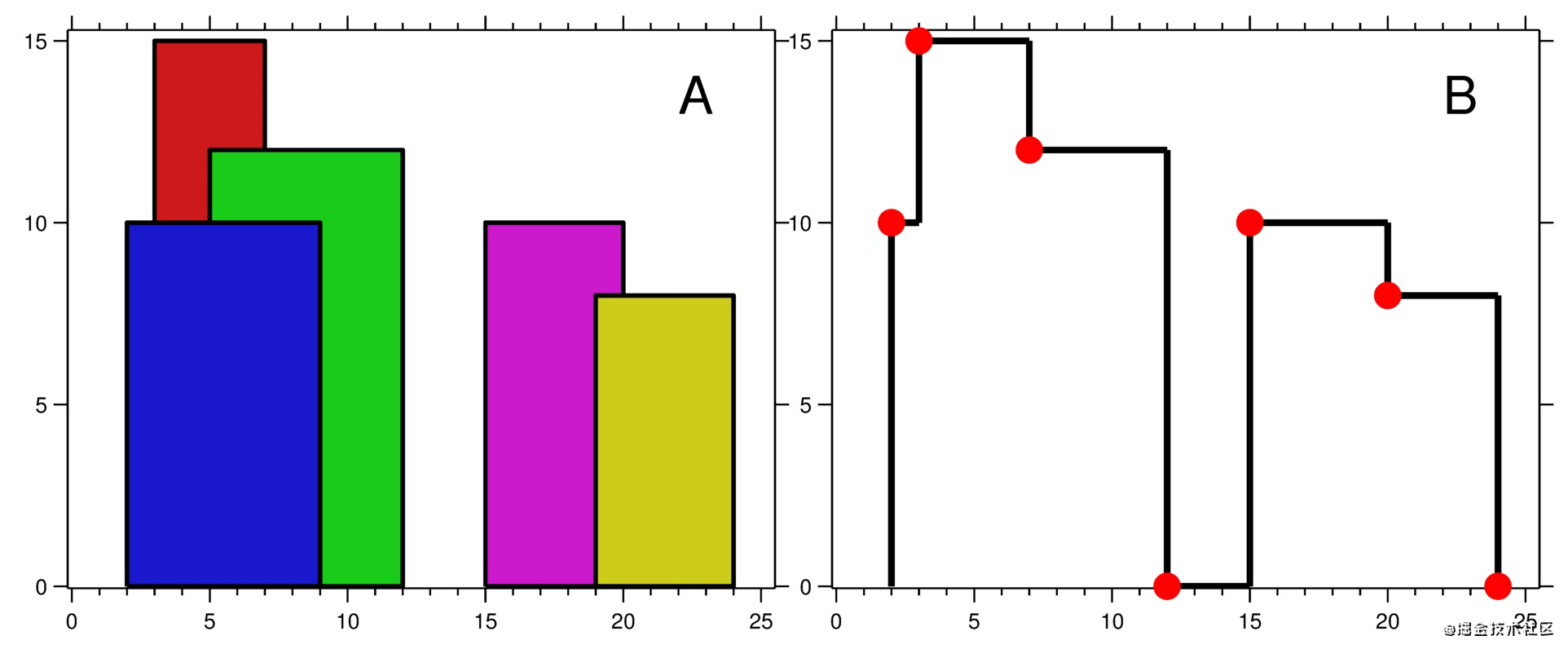
輸入：buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
輸出：[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解釋：
圖 A 顯示輸入的所有建筑物的位置和高度，
圖 B 顯示由這些建筑物形成的天際線。圖 B 中的紅點表示輸出列表中的關鍵點。
示例 2：輸入：buildings = [[0,2,3],[2,5,3]]
輸出：[[0,3],[5,0]]

解題思路

通過觀察我們可以得出

• 關鍵點總是來源于建筑物的左邊緣或者右邊緣的
• 相鄰兩個關鍵點之間必定存在高度差
  因此，我們可以只對所有建筑物的左右邊緣進行遍歷，關鍵點只在這些點當中產生

因為最終結果的關鍵點需要按照x坐標進行排序，因此我們先對所有建筑物的左右端點按x坐標進行一次統一的從小到大的排序，x坐標相同的話，按高度從小到大的排序

為了區分建筑物的左右端點，我們可以用負數表示左端點的高度，正數表示右端點的高度

假設遍歷到某個端點cur，大頂堆中存放的是：該端點處于的x坐標，被若干個建筑物

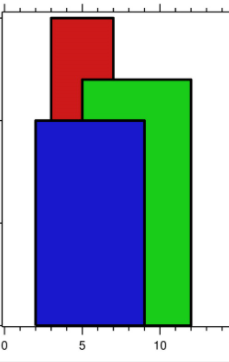
例如，x=7時，存儲的就是3個建筑物的高度，因為當前遍歷的是紅色建筑物的右端點，因此在當前x=7的坐標下，已經不被覆蓋了，所以是2個建筑物的高度，而這兩個建筑物的最大高度是12，和之前關鍵點的最大高度不一致，因此可以判斷出現了關鍵點

總結

簡單來說，在遍歷端點的過程中，通過高度的正負來實現對建筑物左右端點的判斷，遍歷到左端點則進入優先隊列，說明后面的若干個x坐標都被當前高度為h的建筑物覆蓋，遍歷到右端點則退出優先隊列，說明后面的所有x坐標都不會被當前高度為h的建筑物覆蓋。所以通過優先隊列，我們就可以知道，當前的端點的x坐標覆蓋了多少個建筑物，因為最高的建筑物會遮蓋其他低的建筑物，所以我們維護的是一個大頂堆。

又因為關鍵點和前一個關鍵點的高度必然是不一樣的，所以只要當前的堆頂元素和前一個關鍵點的高度不一樣，我們就可以判斷當前x坐標也是一個關鍵點

代碼

class Solution {public List<List<Integer>> getSkyline(int[][] buildings) {List<List<Integer>> res=new ArrayList<>();List<int[]> cnt=new ArrayList<>();for (int[] building : buildings) {cnt.add(new int[]{building[0],-building[2]});cnt.add(new int[]{building[1],building[2]});}int i=0,pre=0;Collections.sort(cnt,(o1, o2) -> o1[0]==o2[0]?o1[1]-o2[1]:o1[0]-o2[0]);PriorityQueue<Integer>priorityQueue=new PriorityQueue<>((o1, o2) -> o2-o1);priorityQueue.add(0);for (int[] cur : cnt) {if(cur[1]<0){priorityQueue.add(-cur[1]);}else{priorityQueue.remove(cur[1]);}int h=priorityQueue.peek();if(h!=pre){res.add(Arrays.asList(cur[0],h));pre=h;}}return res;}
}