本系列教程適用于沒有任何pytorch的同學（簡單的python語法還是要的），從代碼的表層出發挖掘代碼的深層含義，理解具體的意思和內涵。pytorch的很多函數看著非常簡單，但是其中包含了很多內容，不了解其中的意思就只能【看懂代碼】，無法【理解代碼】。

官方定義

nn.Linear 是 PyTorch 中用于創建線性層的類。線性層也被稱為全連接層，它將輸入與權重矩陣相乘并加上偏置，然后通過激活函數進行非線性變換。

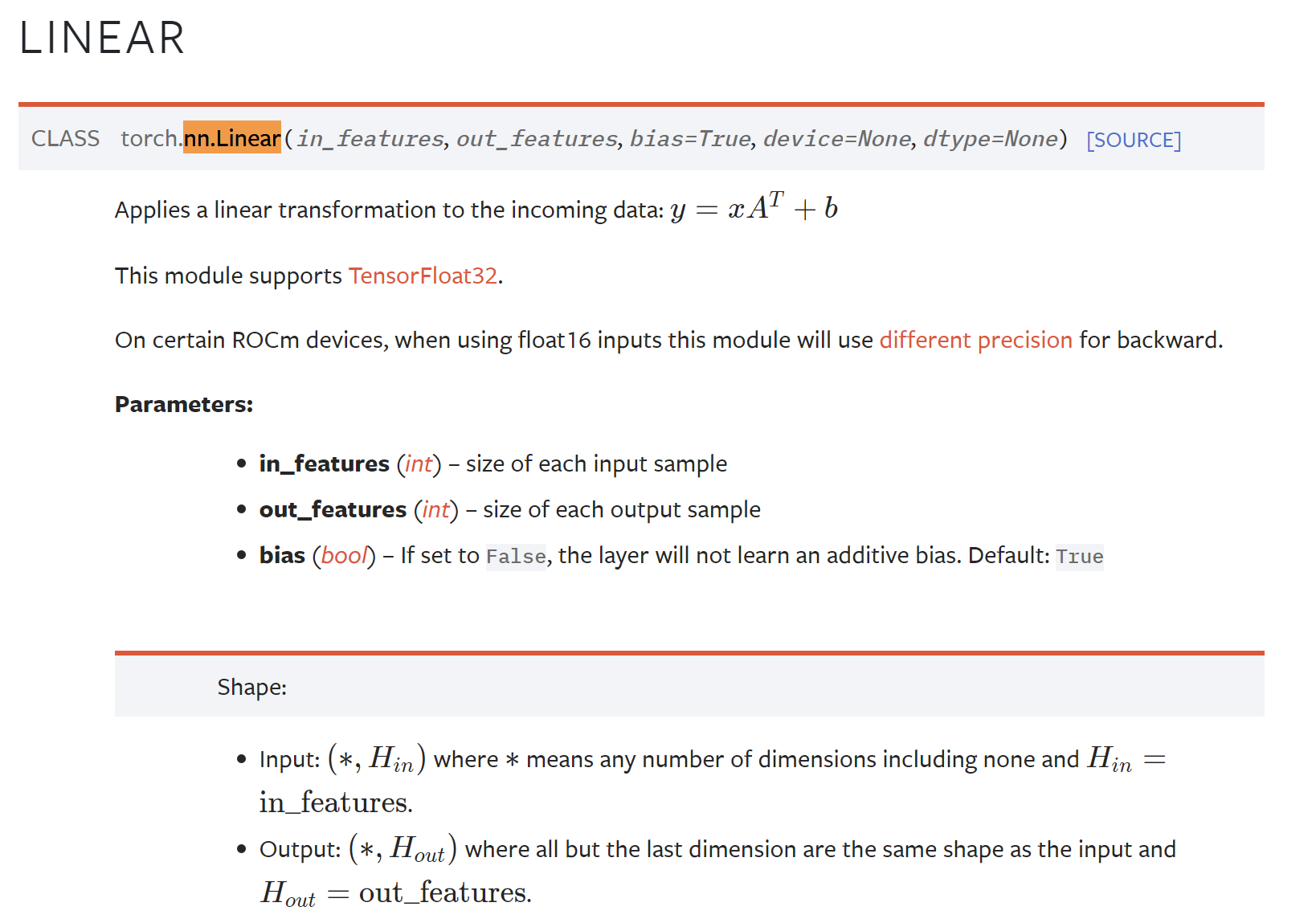
官方的文檔如下，torch.nn.Linear:

demo1

下面是一個官方文檔給出的例子：

m = nn.Linear(20, 30)
input = torch.randn(128, 20)
output = m(input)
print(output.size())

輸出的結果：

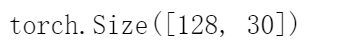
首先，輸出[128, 20]的張量，經過一個[20, 30]的線性層，變成[128, 30]的張量。
可以理解為矩陣的乘法，也就是矩陣的"外積"，矩陣的叉乘，第一個矩陣的行數與第二個矩陣的列數相同。

demo2

input_data = torch.Tensor([[1, 2, 3], [4, 5, 6]]) # [2, 3] 
m = nn.Linear(3, 2)
output = m(input_data)
print(output) # [2, 2]

輸出：

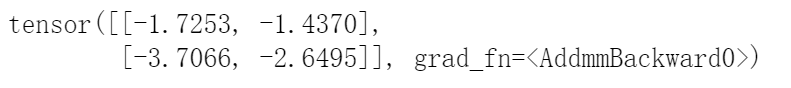
可以看看nn.Linear(3, 2)的參數：

for param in m.parameters():print(param)

輸出：

結合參數，其實本身它們的計算就是矩陣的乘法：

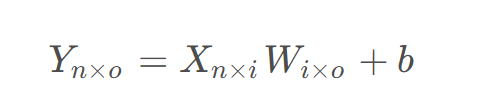
輸入X為[n, i]的矩陣，經過W為[i,0]的矩陣，加上b的偏置得到Y為[n,o]的矩陣。

計算的思路也比較簡單：
output[0][0] = [1, 2, 3] * [0.2888, -0.4596, -0,4896] + 0.3740 = -1.7253
output[0][1] = [1, 2, 3] * [0.4730, -0.4033, -0.4739] + 0.3182 = -1.4370
output[1][0] = [4, 5, 6] * [0.2888, -0.4596, -0,4896] + 0.3740 = -3.7066
output[1][1] = [4, 5, 6] * [0.4730, -0.4033, -0.4739] + 0.3182 = -2.6495

通過input和param的對比，我們可以很輕松地理解實際上就是矩陣的乘法操作。而模型在訓練過程中就是不斷調整param的參數使得輸出的張量符合訓練集的需求。