An outlier is a data point in a data set that is distant from all other observations. A data point that lies outside the overall distribution of the dataset. Or in a layman term, we can say, an outlier is something that behaves differently from the combination/collection of the data.

離群值是數據集中的一個數據點，該數據點與所有其他觀察值相距較遠。 位于數據集總體分布之外的數據點。 或用外行術語來說，離群值是與數據的組合/收集不同的行為。

Outliers can be very informative about the subject-area and data collection process. It’s essential to understand how outliers occur and whether they might happen again as a normal part of the process or study area. To understand outliers, we need to go through these points:

異常值可能對主題區域和數據收集過程很有幫助。 了解離群值如何發生以及在過程或研究區域的正常部分是否會再次發生離群值至關重要。 要了解異常值，我們需要經歷以下幾點：

• what causes the outliers?
  是什么導致異常值？
• Impact of the outlier
  離群值的影響
• Methods to Identify outliers
  識別異常值的方法

是什么導致異常值？ (What causes the outliers?)

Before dealing with the outliers, one should know what causes them. There are three causes for outliers — data entry/An experiment measurement errors, sampling problems, and natural variation.

在處理異常值之前，應該知道是什么導致了異常值。 造成異常的原因有三點：數據輸入/實驗測量錯誤，采樣問題和自然變化。

1. Data entry /An experimental measurement error
   數據輸入/實驗測量錯誤

An error can occur while experimenting/entering data. During data entry, a typo can type the wrong value by mistake. Let us consider a dataset of age, where we found a person age is 356, which is impossible. So this is a Data entry error.

實驗/輸入數據時可能會發生錯誤。 在數據輸入期間，錯字可能會錯誤輸入錯誤的值。 讓我們考慮年齡的數據集，我們發現一個人的年齡是356，這是不可能的。 因此，這是一個數據輸入錯誤。

These types of errors are easy to identify. If you determine that an outlier value is an error, we can fix this error by deleting the data point because you know it’s an incorrect value.

這些類型的錯誤很容易識別。 如果您確定異常值是錯誤的，我們可以通過刪除數據點來解決此錯誤，因為您知道該值是錯誤的。

2. Sampling problems

2.抽樣問題

Outliers can occur while collecting random samples. Let us consider an example where we have records of bone density of various subjects, but there is an unusual growth of bone in a subject, after analyzing this has been discovered that the subject had diabetes, which affects bone health. The goal was to model bone density growth in girls with no health conditions that affect bone growth. Since the data is not a part of the target population so we will not consider this.

收集隨機樣本時可能會出現異常值。 讓我們考慮一個示例，在該示例中，我們記錄了各個受試者的骨密度，但是在分析了該受試者患有糖尿病并影響骨骼健康之后，該受試者的骨骼異常生長。 目的是在沒有影響骨骼生長的健康狀況的女孩中模擬骨骼密度的增長。 由于數據不是目標人群的一部分，因此我們不會考慮這一點。

3. Natural variation

3.自然變異

Suppose we need to check the reliability of a machine. The normal process includes standard materials, manufacturing settings, and conditions. If something unusual happens during a portion of the study, such as a power failure or a machine setting drifting off the standard value, it can affect the products. These abnormal manufacturing conditions can cause outliers by creating products with atypical strength values. Products manufactured under these unusual conditions do not reflect your target population of products from the normal process. Consequently, you can legitimately remove these data points from your dataset.

假設我們需要檢查機器的可靠性。 正常過程包括標準材料，制造設置和條件。 如果在研究的一部分過程中發生異常情況，例如電源故障或機器設置偏離標準值，則可能會影響產品。 這些異常的制造條件可能會通過創建具有非典型強度值的產品而導致異常值。 在這些異常條件下制造的產品不能反映正常過程中目標產品的數量。 因此，您可以合法地從數據集中刪除這些數據點。

離群值的影響 (Impact of the outlier)

Outliers can change the results of the data analysis and statistical modeling. Following are some impacts of outliers in the data set:

離群值可以更改數據分析和統計建模的結果。 以下是數據集中異常值的一些影響：

• It may cause a significant impact on the mean and the standard deviation
  可能會對平均值和標準偏差產生重大影響
• If the outliers are non-randomly distributed, they can decrease normality
  如果離群值是非隨機分布的，則它們可能會降低正態性
• They can bias or influence estimates that may be of substantive interest
  它們可能會偏向或影響可能具有實質意義的估計
• They can also impact the basic assumption of Regression, ANOVA, and other statistical model assumptions.
  它們還會影響回歸，ANOVA和其他統計模型假設的基本假設。

To understand the impact deeply, let’s take an example to check what happens to a data set with and without outliers in the data set.

為了深入了解其影響，讓我們舉一個例子來檢查在數據集中有無異常時數據集會發生什么情況。

Let’s examine what can happen to a data set with outliers. For the sample data set:

讓我們研究帶有異常值的數據集會發生什么。 對于樣本數據集：

1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4

1，1，2，2，2，2，3，3，3，4，4

We find the following mean, median, mode, and standard deviation:

我們發現以下平均值，中位數，眾數和標準差：

Mean = 2.58

均值= 2.58

Median = 2.5

中位數= 2.5

Mode = 2

模式= 2

Standard Deviation = 1.08

標準偏差= 1.08

If we add an outlier to the data set:

如果我們向數據集添加離群值：

1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 400

1，1，2，2，2，2，3，3，3，4，4，400

The new values of our statistics are:

我們的統計信息的新值是：

Mean = 35.38

均值= 35.38

Median = 2.5

中位數= 2.5

Mode = 2

模式= 2

Standard Deviation = 114.74

標準偏差= 114.74

As you can see, having outliers often has a significant effect on your mean and standard deviation.

如您所見，離群值通常會對平均值和標準差產生重大影響。

識別異常值的方法 (Methods to Identify outliers)

There are various ways to identify outliers in a dataset, following are some of them:

在數據集中識別異常值的方法有多種，以下是其中的一些方法：

1. Sorting the data
   排序數據
2. Using graphical Method
   使用圖形方法
3. Using z score
   使用z分數
4. Using the IQR interquartile range
   使用IQR四分位距

排序數據 (Sorting the data)

Sorting the dataset is the simplest and effective method to check unusual value. Let us consider an example of age dataset:

對數據集進行排序是檢查異常值的最簡單有效的方法。 讓我們考慮年齡數據集的示例：

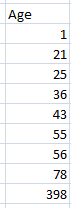
In the above dataset, we have sort the age dataset and get to know that 398 is an outlier. Sorting data method is most effective on the small dataset.

在上面的數據集中，我們對年齡數據集進行了排序，并且知道398是一個離群值。 排序數據方法對小型數據集最有效。

使用圖形方法 (Using graphical Method)

We can detect outliers with the help of graphical representation like Scatter plot and Boxplot.

我們可以借助散點圖和Boxplot等圖形表示來檢測異常值。

1. Scatter Plot

1.散點圖

Scatter plots often have a pattern. We call a data point an outlier if it doesn’t fit the pattern. Here we have a scatter plot of Weight vs height. Notice how two of the points don’t fit the pattern very well. There is no special rule that tells us whether or not a point is an outlier in a scatter plot. When doing more advanced statistics, it may become helpful to invent a precise definition of “outlier”.

散點圖通常具有某種模式。 如果數據點不適合模式，我們稱其為離群值 。 這是重量與高度的散點圖。 請注意，有兩個點不太適合該模式。 沒有特殊的規則可以告訴我們點在散點圖中是否是異常值。 在進行更高級的統計時，發明精確定義“異常值”可能會有所幫助。

2. Box-Plot

2.箱線圖

Box-plot is one of the most effective ways of identifying Outliers in a dataset. When reviewing a box plot, an outlier is defined as a data point that is located outside the box of the box plot. As seen in the box plot of bill vs days. Box-Plot uses the Interquartile range(IQR) to detect outliers.

箱線圖是識別數據集中異常值的最有效方法之一。 查看箱形圖時，離群值定義為位于箱形圖框外部的數據點。 如票據與天數的方框圖所示。 箱線圖使用四分位間距(IQR)來檢測離群值。

使用z分數 (Using z-score)

Z-score (also called a standard score) gives you an idea of how many standard deviations away a data point is from the mean.. But more technically it’s a measure of how many standard deviations below or above the population mean a raw score is.

Z分數(也稱為標準分數 )使您了解一個數據點與平均值之間有多少標準偏差。但是從技術上講，它衡量的是低于或高于總體的多少標準偏差表示原始分數是多少。 。

Z score = (x -mean) / std. deviation

Z分數=(x-均值)/ std。 偏差

In a normal distribution, it is estimated that

在正態分布中，估計

68% of the data points lie between +/- 1 standard deviation.

68％的數據點位于+/- 1標準偏差之間。

95% of the data points lie between +/- 2 standard deviation.

95％的數據點在+/- 2標準偏差之間。

99.7% of the data points lie between +/- 3 standard deviation.

99.7％的數據點位于+/- 3標準偏差之間。

Formula for Z score = (Observation — Mean)/Standard Deviation

Z分數的公式=(觀測值–平均值)/標準差

z = (X — μ) / σ

z =(X —μ)/σ

Let us consider a dataset:

讓我們考慮一個數據集：

使用IQR四分位距 (Using the IQR interquartile range)

Interquartile range(IQR), is just the width of the box in the box-plot which can be used as a measure of how spread out the values are. An outlier is any value that lies more than one and a half times the length of the box from either end of the box.

四分位數間距(IQR)只是箱形圖中箱形的寬度，可用作度量值分布的程度。 離群值是從框的兩端到框長度的一半以上的任何值。

Steps

腳步

1. Arrange the data in increasing order
   按升序排列數據
2. Calculate first(q1) and third quartile(q3)
   計算第一個(q1)和第三個四分位數(q3)
3. Find interquartile range (q3-q1)
   查找四分位數范圍(q3-q1)
4. Find lower bound q1*1.5
   求下界q1 * 1.5
5. Find upper bound q3*1.5
   求上限q3 * 1.5

Anything that lies outside of lower and upper bound is an outlier

上下限以外的任何東西都是異常值

Let us take the same example as of Z-score:

讓我們以與Z分數相同的示例為例：

As you can see we have found Lower and upper values that is: 7.5 and 19.5, so anything that lies outside these values is an outlier.

如您所見，我們發現下限值和上限值分別是：7.5和19.5，因此超出這些值的任何值都是異常值。

This is all we have about outliers, I hope you enjoyed reading. Thank you

這就是關于異常值的全部內容，希望您喜歡閱讀。 謝謝