375. 猜數字大小 II
我們正在玩一個猜數游戲,游戲規則如下:
- 我從?1?到 n 之間選擇一個數字。
- 你來猜我選了哪個數字。
- 如果你猜到正確的數字,就會 贏得游戲 。
- 如果你猜錯了,那么我會告訴你,我選的數字比你的 更大或者更小 ,并且你需要繼續猜數。
- 每當你猜了數字 x 并且猜錯了的時候,你需要支付金額為 x 的現金。如果你花光了錢,就會 輸掉游戲 。
給你一個特定的數字 n ,返回能夠 確保你獲勝 的最小現金數,不管我選擇那個數字 。
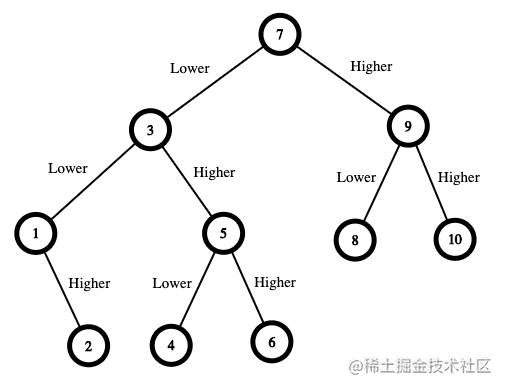
示例 1:輸入:n = 10
輸出:16
解釋:制勝策略如下:
- 數字范圍是 [1,10] 。你先猜測數字為 7 。- 如果這是我選中的數字,你的總費用為 $0 。否則,你需要支付 $7 。- 如果我的數字更大,則下一步需要猜測的數字范圍是 [8,10] 。你可以猜測數字為 9 。- 如果這是我選中的數字,你的總費用為 $7 。否則,你需要支付 $9 。- 如果我的數字更大,那么這個數字一定是 10 。你猜測數字為 10 并贏得游戲,總費用為 $7 + $9 = $16 。- 如果我的數字更小,那么這個數字一定是 8 。你猜測數字為 8 并贏得游戲,總費用為 $7 + $9 = $16 。- 如果我的數字更小,則下一步需要猜測的數字范圍是 [1,6] 。你可以猜測數字為 3 。- 如果這是我選中的數字,你的總費用為 $7 。否則,你需要支付 $3 。- 如果我的數字更大,則下一步需要猜測的數字范圍是 [4,6] 。你可以猜測數字為 5 。- 如果這是我選中的數字,你的總費用為 $7 + $3 = $10 。否則,你需要支付 $5 。- 如果我的數字更大,那么這個數字一定是 6 。你猜測數字為 6 并贏得游戲,總費用為 $7 + $3 + $5 = $15 。- 如果我的數字更小,那么這個數字一定是 4 。你猜測數字為 4 并贏得游戲,總費用為 $7 + $3 + $5 = $15 。- 如果我的數字更小,則下一步需要猜測的數字范圍是 [1,2] 。你可以猜測數字為 1 。- 如果這是我選中的數字,你的總費用為 $7 + $3 = $10 。否則,你需要支付 $1 。- 如果我的數字更大,那么這個數字一定是 2 。你猜測數字為 2 并贏得游戲,總費用為 $7 + $3 + $1 = $11 。
在最糟糕的情況下,你需要支付 $16 。因此,你只需要 $16 就可以確保自己贏得游戲。示例 2:輸入:n = 1
輸出:0
解釋:只有一個可能的數字,所以你可以直接猜 1 并贏得游戲,無需支付任何費用。示例 3:輸入:n = 2
輸出:1
解釋:有兩個可能的數字 1 和 2 。
- 你可以先猜 1 。- 如果這是我選中的數字,你的總費用為 $0 。否則,你需要支付 $1 。- 如果我的數字更大,那么這個數字一定是 2 。你猜測數字為 2 并贏得游戲,總費用為 $1 。
最糟糕的情況下,你需要支付 $1 。解題思路
- 數組定義:dp[i][j]代表從區間[i,j]里面猜數字,能夠 確保獲勝 的最小現金數。
- 初始化:當i==j時,只能猜一個數字,所以必定勝利,不需要花費任何現金,當i>j時,不存在實際意義
- 狀態轉移:從區間[i,j]里面猜數字,遍歷所有可能的選擇,在選擇完猜測的數字k以后,選擇花費更大的區間進行下一輪的猜數字max(dp[i][k-1],dp[k+1][j]),因為我們必須確保能夠獲勝,所以考慮的都是最壞的情況
代碼
class Solution {
public:int getMoneyAmount(int n) {vector<vector<int>> dp(n+1,vector<int>(n+1));for (int i = n-1; i >=1; i--) {for (int j = i+1; j <=n ; ++j) {int m=INT_MAX;for (int k = i; k <j ; ++k) {m=min(m,k+max(dp[i][k-1],dp[k+1][j]));}dp[i][j]=m;}}return dp[1][n];}
};




)




)
)



)




