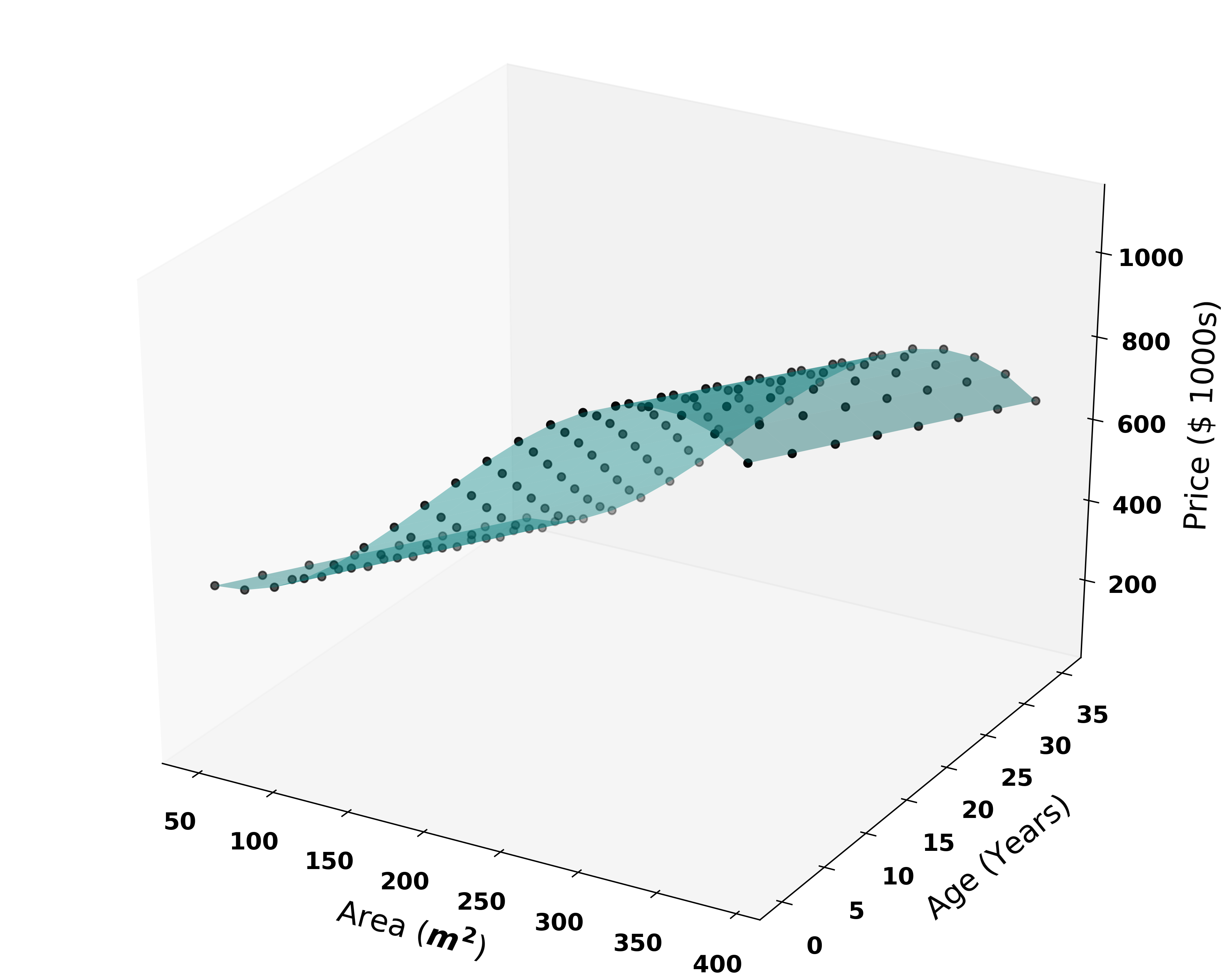
Let’s start with an example. We want to predict the Price of a home based on the Area and Age. The function below was used to generate Home Prices and we can pretend this is “real-world data” and our “job” is to create a model which will predict the Price based on Area and Age:

讓我們從一個例子開始。 我們想根據面積和年齡來預測房屋價格。 下面的函數用于生成房屋價格，我們可以假裝這是“真實數據”，而我們的“工作”是創建一個模型，該模型將根據面積和年齡預測價格：

價格= -3 *面積-10 *年齡+ 0.033 *面積2-0.0000571 *面積3+ 500 (Price = -3*Area -10*Age + 0.033*Area2 -0.0000571*Area3 + 500)

線性模型 (Linear Model)

Let’s suppose we just want to create a very simple Linear Regression model that predicts the Price using slope coefficients c1 and c2 and the y-intercept c0:

假設我們只想創建一個非常簡單的線性回歸模型，該模型使用斜率系數c1和c2以及y軸截距 c0來預測價格：

Price = c1*Area+c2*Age + c0

價格= c1 *面積+ c2 *年齡+ c0

We’ll load the data and implement Scikit-Learn’s Linear Regression. Behind the scenes, model coefficients (c0, c1, c2) are computed by minimizing the sum of squares of individual errors between target variable y and the model prediction:

我們將加載數據并實現Scikit-Learn的線性回歸 。 在幕后，通過最小化目標變量y與模型預測之間的各個誤差的平方和來計算模型系數(c0，c1，c2)：

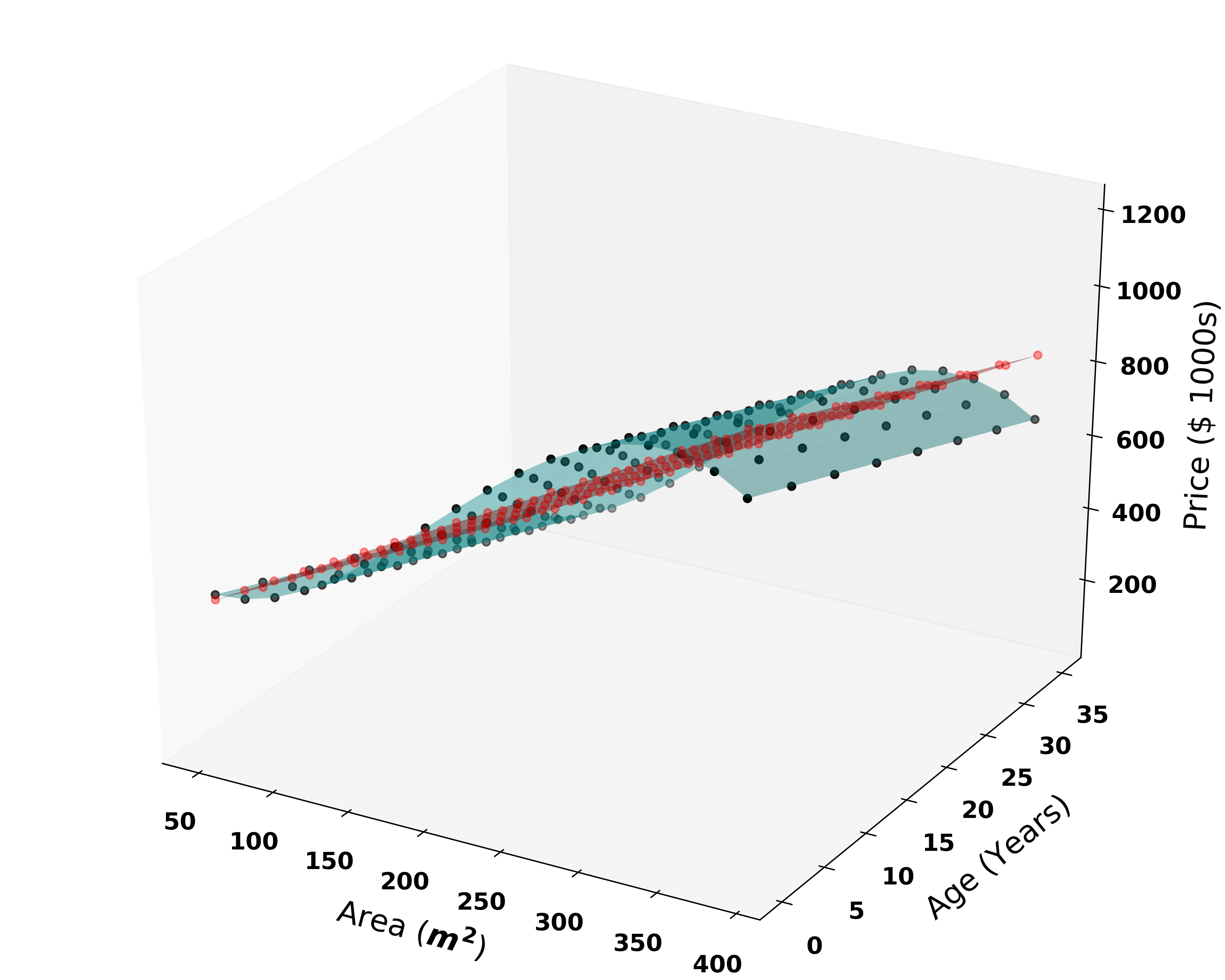
But you see we don’t do a very good job with this model.

但是您會看到我們在此模型上做得不好。

多項式回歸模型 (Polynomial Regression Model)

Next, let’s implement the Polynomial Regression model because it’s the right tool for the job. Rewriting the initial function used to generate the home Prices, where x1 = Area, and x2 = Age, we get the following:

接下來，讓我們實現多項式回歸模型，因為它是這項工作的正確工具。 重寫用于生成房屋價格的初始函數，其中x1 =面積，x2 =年齡，我們得到以下信息：

價格= -3 * x1 -10 * x2 + 0.033 *x12-0.0000571 *x13+ 500 (Price = -3*x1 -10*x2 + 0.033*x12 -0.0000571*x13 + 500)

So now instead of the Linear model (Price = c1*x1 +c2*x2 + c0), Polynomial Regression requires we transform the variables x1 and x2. For example, if we want to fit a 2nd-degree polynomial, the input variables are transformed as follows:

因此，現在多項式回歸代替線性模型(價格= c1 * x1 + c2 * x2 + c0)，需要轉換變量x1和x2。 例如，如果要擬合二階多項式，則輸入變量的轉換如下：

1, x1, x2, x12, x1x2, x22

1，x1，x2，x12，x1x2，x22

But our 3rd-degree polynomial version will be:

但是我們的三階多項式將是：

1, x1, x2, x12, x1x2, x22, x13, x12x2, x1x22, x23

1，x1，x2，x12，x1x2，x22，x13，x12x2，x1x22，x23

Then we can use the Linear model with the polynomially transformed input features and create a Polynomial Regression model in the form of:

然后，我們可以將線性模型與多項式轉換后的輸入特征一起使用，并創建以下形式的多項式回歸模型：

Price = 0*1 + c1*x1 + c2*x2 +c3*x12 + c4*x1x2 + … + cn*x23 + c0

價格= 0 * 1 + c1 * x1 + c2 * x2 + c3 *x12+ c4 * x1x2 +…+ cn *x23+ c0

(0*1 relates to the bias (1s) column)

(0 * 1與偏置(1s)列有關)

After training the model on the data we can check the coefficients and see if they match our original function used to generate home prices:

在對數據進行模型訓練之后，我們可以檢查系數，看看它們是否與用于生成房屋價格的原始函數匹配：

Original Function:

原始功能：

價格= -3 * x1 -10 * x2 + 0.033 *x12-0.0000571 *x13+ 500 (Price = -3*x1 -10*x2 + 0.033*x12 -0.0000571*x13 + 500)

Polynomial Regression model coefficients:

多項式回歸模型系數：

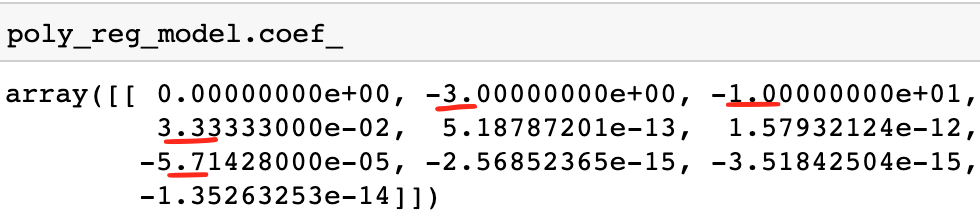
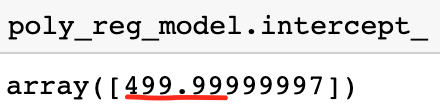
and indeed they match!

確實匹配！

Now you can see we do a much better job.

現在您可以看到我們做得更好。

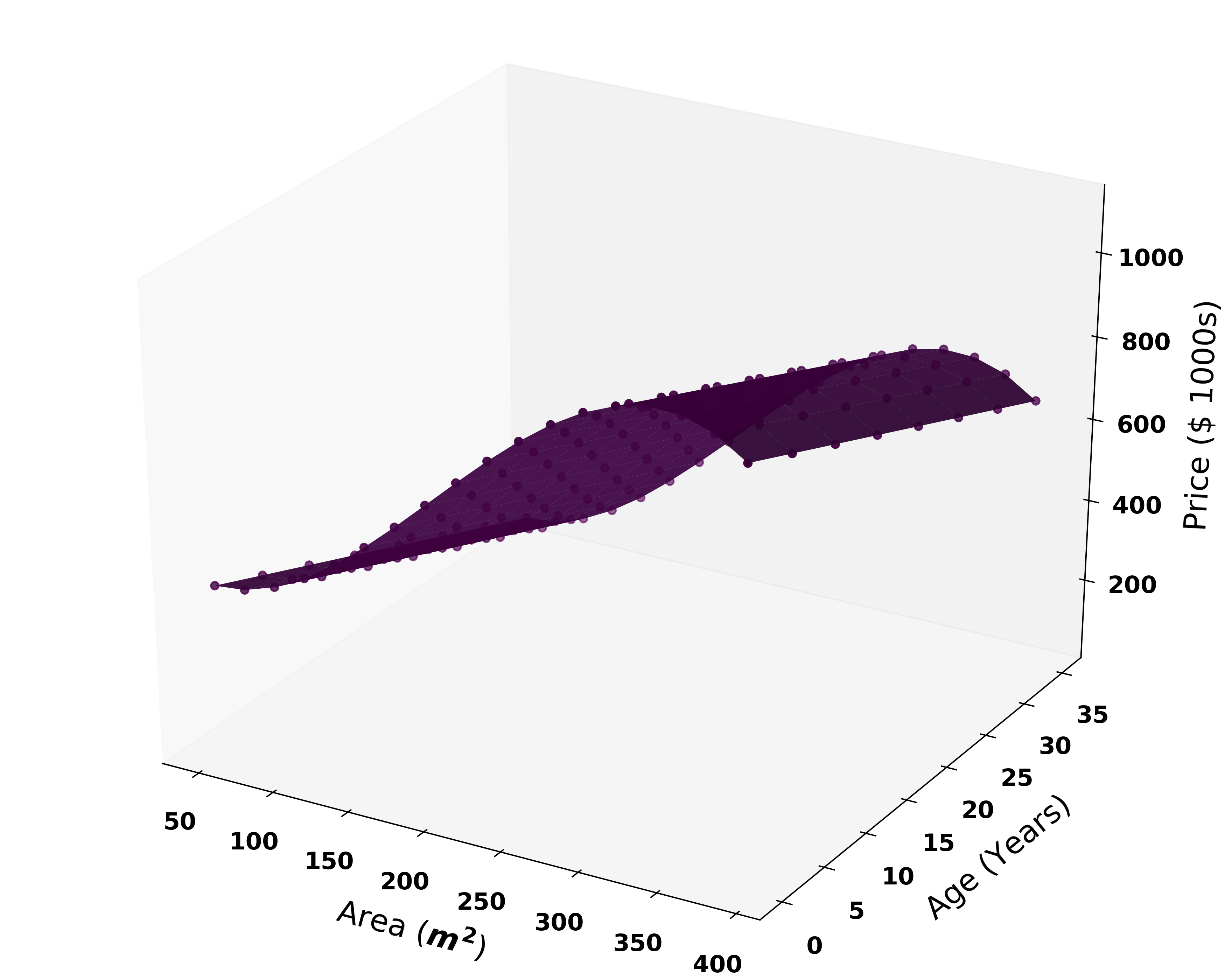
And there you have it, now you know how to implement a Polynomial Regression model in Python. Entire code can be found here.

有了它，現在您知道如何在Python中實現多項式回歸模型。 完整的代碼可以在這里找到。

結束語 (Closing remarks)

• If this were a real-world ML task, we should have split data into training and testing sets, and evaluated the model on the testing set.
  如果這是現實世界中的ML任務，我們應該將數據分為訓練和測試集，并在測試集上評估模型。
• It’s better to use other accuracy metrics such as RMSE because MRE will be undefined if there’s a 0 in the y values.
  最好使用其他精度度量標準，例如RMSE，因為如果y值中為0，則MRE將不確定。