應該是一道中等難度的點分?麻煩在一些細節。
題目描述
lrb有一棵樹,樹的每個節點有個顏色。給一個長度為n的顏色序列,定義s(i,j) 為i 到j 的顏色數量。以及
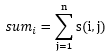
現在他想讓你求出所有的sum[i]
輸入輸出格式
輸入格式:
第一行為一個整數n,表示樹節點的數量
第二行為n個整數,分別表示n個節點的顏色c[1],c[2]……c[n]
接下來n-1行,每行為兩個整數x,y,表示x和y之間有一條邊
輸出格式:
輸出n行,第i行為sum[i]
說明
sum[1]=s(1,1)+s(1,2)+s(1,3)+s(1,4)+s(1,5)=1+2+3+2+2=10
sum[2]=s(2,1)+s(2,2)+s(2,3)+s(2,4)+s(2,5)=2+1+2+1+3=9
sum[3]=s(3,1)+s(3,2)+s(3,3)+s(3,4)+s(3,5)=3+2+1+2+3=11
sum[4]=s(4,1)+s(4,2)+s(4,3)+s(4,4)+s(4,5)=2+1+2+1+3=9
sum[5]=s(5,1)+s(5,2)+s(5,3)+s(5,4)+s(5,5)=2+3+3+3+1=12對于40%的數據,n<=2000
對于100%的數據,1<=n,c[i]<=10^5
題目分析
想法一:按顏色拆貢獻
這里應該是有一種小顏色大顏色的分塊套路的。但是這個想法我只能解決全局路徑的數量和,并不會落實到點的詢問。
想法二:點分治
目前尚未歸結出點分治適用的具體問題范圍……不過這一題是可以用點分解決的。
考慮每一層點分樹,我們只需要對它的節點處理貢獻。這里的貢獻分為兩部分:重心答案;經過重心的路徑對子樹的貢獻。
重心的答案只需要以它自身為根,遍歷一邊該層點分樹即可。子樹內的答案處理要略微麻煩一些,需要分顏色來考慮貢獻。記$colCnt[i]$為所有以重心為起點的路徑中,含有顏色$i$的路徑條數。然后首先假定子樹內所有點的答案都為$\sum colCnt[i]$,再容斥考慮重心到子樹路徑上的顏色所產生的貢獻。
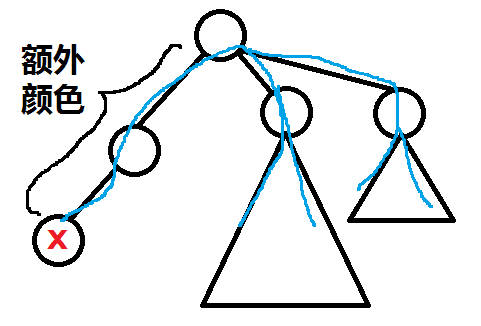
記當前點分樹中除去正在處理的子樹的大小為$outTot$,那么對于子樹內點$x$,由于它具有顏色$c[x]$,所以對自身的答案有一個$outTot-colCnt[c[x]]$的貢獻。并且,這一個貢獻對于$x$的子樹也是一概適用的,所以這一個標記要差分式地下傳。
整體思路就是這些。這一題的點分涉及到例如“子樹結構的重定向”或是“兩個顏色桶并存”的一些細節問題,所以實現上面可能有一定的難度。
(話說這題的碼風怎么這么丑)
?
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const int maxn = 100035; 4 const int maxm = 200035; 5 6 ll ans[maxn]; 7 int n,bloTot,outTot,c[maxn]; 8 int size[maxn],son[maxn],root; 9 int edgeTot,head[maxn],nxt[maxm],edges[maxm]; 10 int cols,cnt,cl,col[maxn],colTmp[maxn],colTim[maxn],colCnt[maxn],subCnt[maxn]; 11 bool colEx[maxn],divEx[maxn]; 12 13 int read() 14 { 15 char ch = getchar(); 16 int num = 0, fl = 1; 17 for (; !isdigit(ch); ch=getchar()) 18 if (ch=='-') fl = -1; 19 for (; isdigit(ch); ch=getchar()) 20 num = (num<<1)+(num<<3)+ch-48; 21 return num*fl; 22 } 23 void addedge(int u, int v) 24 { 25 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 26 edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot; 27 } 28 void getRoot(int x, int fa) 29 { 30 size[x] = 1, son[x] = 0; 31 for (int i=head[x]; i!=-1; i=nxt[i]) 32 { 33 int v = edges[i]; 34 if (divEx[v]||v==fa) continue; 35 getRoot(v, x), size[x] += size[v]; 36 son[x] = std::max(son[x], size[v]); 37 } 38 son[x] = std::max(son[x], bloTot-size[x]); 39 if (son[x] < son[root]) root = x; 40 } 41 void colDfs(int x, int fa, int *cnt) 42 { 43 if (!colEx[c[x]]) colEx[c[x]] = 1, col[++cols] = c[x]; 44 if ((++colTim[c[x]])==1) cnt[c[x]] += size[x]; 45 for (int i=head[x]; i!=-1; i=nxt[i]) 46 if ((!divEx[edges[i]])&&(edges[i]!=fa)) 47 colDfs(edges[i], x, cnt); 48 --colTim[c[x]]; 49 } 50 void colClear() 51 { 52 for (int i=1; i<=cl; i++) colEx[colTmp[i]] = 0; 53 cols = 0; 54 } 55 void modify(int x, int fa, ll tag) 56 { 57 if ((++colTim[c[x]])==1) tag += outTot-colCnt[c[x]]; 58 ans[x] += tag+cnt; 59 for (int i=head[x]; i!=-1; i=nxt[i]) 60 { 61 int v = edges[i]; 62 if (v==fa||divEx[v]) continue; 63 modify(v, x, tag); 64 } 65 --colTim[c[x]]; 66 } 67 void calc(int rt) //核心操作在這里 68 { 69 colClear(), getRoot(rt, 0); 70 colDfs(rt, 0, colCnt); 71 cnt = 0, cl = cols; 72 for (int i=1; i<=cols; i++) 73 cnt += colCnt[col[i]], colTmp[i] = col[i]; 74 ans[rt] += cnt; 75 for (int i=head[rt]; i!=-1; i=nxt[i]) 76 { 77 int v = edges[i]; 78 if (divEx[v]) continue; 79 for (int j=1; j<=cl; j++) subCnt[colTmp[j]] = 0; //及時清除數組 80 colClear(); 81 colEx[c[rt]] = 1; 82 colDfs(v, rt, subCnt); //統計子樹內的含顏色i路徑條數 83 colEx[c[rt]] = 0; 84 colCnt[c[rt]] -= size[v], cnt -= size[v]; //除去重心出發的路徑 85 for (int j=1; j<=cols; j++) 86 { 87 colCnt[col[j]] -= subCnt[col[j]]; //除去子樹內的路徑(因為考慮子樹外路徑) 88 cnt -= subCnt[col[j]]; 89 } 90 outTot = size[rt]-size[v], modify(v, rt, 0); //對子樹內累加貢獻 91 colCnt[c[rt]] += size[v], cnt += size[v]; //恢復處理子樹前狀態 92 for (int j=1; j<=cols; j++) 93 { 94 colCnt[col[j]] += subCnt[col[j]]; 95 cnt += subCnt[col[j]]; 96 } 97 } 98 for (int i=1; i<=cl; i++) 99 colCnt[colTmp[i]] = 0; //colTmp[]的作用;清空colCnt[] 100 } 101 void deal(int rt) 102 { 103 calc(rt), divEx[rt] = 1; 104 for (int i=head[rt]; i!=-1; i=nxt[i]) 105 { 106 int v = edges[i]; 107 if (divEx[v]) continue; 108 root = 0, bloTot = size[v]; 109 getRoot(v, 0), deal(root); 110 } 111 } 112 int main() 113 { 114 memset(head, -1, sizeof head); 115 n = read(), son[0] = n; 116 for (int i=1; i<=n; i++) c[i] = read(); 117 for (int i=1; i<n; i++) addedge(read(), read()); 118 bloTot = n, getRoot(1, 0), deal(root); 119 for (int i=1; i<=n; i++) printf("%lld\n",ans[i]); 120 return 0; 121 }
?
?
?
END




、遠程代碼執行漏洞(CVE-2017-12615)


)

)

)


)
)



