機器學習算法太多了,分類、回歸、聚類、推薦、圖像識別領域等等,要想找到一個合適算法真的不容易,所以在實際應用中,我們一般都是采用啟發式學習方式來實驗。通常最開始我們都會選擇大家普遍認同的算法,諸如SVM,GBDT,Adaboost,現在深度學習很火熱,神經網絡也是一個不錯的選擇。假如你在乎精度(accuracy)的話,最好的方法就是通過交叉驗證(cross-validation)對各個算法一個個地進行測試,進行比較,然后調整參數確保每個算法達到最優解,最后選擇最好的一個。但是如果你只是在尋找一個“足夠好”的算法來解決你的問題,或者這里有些技巧可以參考,下面來分析下各個算法的優缺點,基于算法的優缺點,更易于我們去選擇它。
偏差&方差
在統計學中,一個模型好壞,是根據偏差和方差來衡量的,所以我們先來普及一下偏差和方差:
偏差:描述的是預測值(估計值)的期望E’與真實值Y之間的差距。偏差越大,越偏離真實數據。
方差:描述的是預測值P的變化范圍,離散程度,是預測值的方差,也就是離其期望值E的距離。方差越大,數據的分布越分散。
模型的真實誤差是兩者之和。
如果是小訓練集,高偏差/低方差的分類器(例如,樸素貝葉斯NB)要比低偏差/高方差大分類的優勢大(例如,KNN),因為后者會過擬合。但是,隨著你訓練集的增長,模型對于原數據的預測能力就越好,偏差就會降低,此時低偏差/高方差分類器就會漸漸的表現其優勢(因為它們有較低的漸近誤差),此時高偏差分類器此時已經不足以提供準確的模型了。
當然,你也可以認為這是生成模型(NB)與判別模型(KNN)的一個區別。
為什么說樸素貝葉斯是高偏差低方差?
以下內容引自知乎:
首先,假設你知道訓練集和測試集的關系。簡單來講是我們要在訓練集上學習一個模型,然后拿到測試集去用,效果好不好要根據測試集的錯誤率來衡量。但很多時候,我們只能假設測試集和訓練集的是符合同一個數據分布的,但卻拿不到真正的測試數據。這時候怎么在只看到訓練錯誤率的情況下,去衡量測試錯誤率呢?
由于訓練樣本很少(至少不足夠多),所以通過訓練集得到的模型,總不是真正正確的。(就算在訓練集上正確率100%,也不能說明它刻畫了真實的數據分布,要知道刻畫真實的數據分布才是我們的目的,而不是只刻畫訓練集的有限的數據點)。而且,實際中,訓練樣本往往還有一定的噪音誤差,所以如果太追求在訓練集上的完美而采用一個很復雜的模型,會使得模型把訓練集里面的誤差都當成了真實的數據分布特征,從而得到錯誤的數據分布估計。這樣的話,到了真正的測試集上就錯的一塌糊涂了(這種現象叫過擬合)。但是也不能用太簡單的模型,否則在數據分布比較復雜的時候,模型就不足以刻畫數據分布了(體現為連在訓練集上的錯誤率都很高,這種現象較欠擬合)。過擬合表明采用的模型比真實的數據分布更復雜,而欠擬合表示采用的模型比真實的數據分布要簡單。
在統計學習框架下,大家刻畫模型復雜度的時候,有這么個觀點,認為Error = Bias + Variance。這里的Error大概可以理解為模型的預測錯誤率,是有兩部分組成的,一部分是由于模型太簡單而帶來的估計不準確的部分(Bias),另一部分是由于模型太復雜而帶來的更大的變化空間和不確定性(Variance)。
所以,這樣就容易分析樸素貝葉斯了。它簡單的假設了各個數據之間是無關的,是一個被嚴重簡化了的模型。所以,對于這樣一個簡單模型,大部分場合都會Bias部分大于Variance部分,也就是說高偏差而低方差。
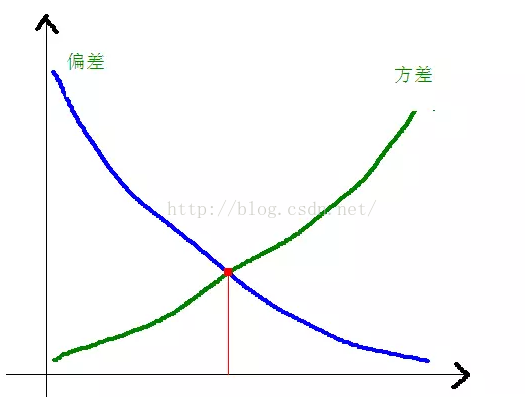
在實際中,為了讓Error盡量小,我們在選擇模型的時候需要平衡Bias和Variance所占的比例,也就是平衡over-fitting和under-fitting。
當模型復雜度上升的時候,偏差會逐漸變小,而方差會逐漸變大。
常見算法優缺點
1.樸素貝葉斯
樸素貝葉斯屬于生成式模型(關于生成模型和判別式模型,主要還是在于是否是要求聯合分布),非常簡單,你只是做了一堆計數。如果注有條件獨立性假設(一個比較嚴格的條件),樸素貝葉斯分類器的收斂速度將快于判別模型,如邏輯回歸,所以你只需要較少的訓練數據即可。即使NB條件獨立假設不成立,NB分類器在實踐中仍然表現的很出色。它的主要缺點是它不能學習特征間的相互作用,用mRMR中R來講,就是特征冗余。引用一個比較經典的例子,比如,雖然你喜歡Brad Pitt和Tom Cruise的電影,但是它不能學習出你不喜歡他們在一起演的電影。
優點:
樸素貝葉斯模型發源于古典數學理論,有著堅實的數學基礎,以及穩定的分類效率。
對小規模的數據表現很好,能個處理多分類任務,適合增量式訓練;
對缺失數據不太敏感,算法也比較簡單,常用于文本分類。
缺點:
需要計算先驗概率;
分類決策存在錯誤率;
對輸入數據的表達形式很敏感。
2.Logistic Regression(邏輯回歸)
屬于判別式模型,有很多正則化模型的方法(L0, L1,L2,etc),而且你不必像在用樸素貝葉斯那樣擔心你的特征是否相關。與決策樹與SVM機相比,你還會得到一個不錯的概率解釋,你甚至可以輕松地利用新數據來更新模型(使用在線梯度下降算法,online gradient descent)。如果你需要一個概率架構(比如,簡單地調節分類閾值,指明不確定性,或者是要獲得置信區間),或者你希望以后將更多的訓練數據快速整合到模型中去,那么使用它吧。
Sigmoid函數:
g(x)=1/(1+exp(-x))
優點:?
實現簡單,廣泛的應用于工業問題上;
分類時計算量非常小,速度很快,存儲資源低;
便利的觀測樣本概率分數;
對邏輯回歸而言,多重共線性并不是問題,它可以結合L2正則化來解決該問題;
缺點:
當特征空間很大時,邏輯回歸的性能不是很好;
容易欠擬合,一般準確度不太高
不能很好地處理大量多類特征或變量;
只能處理兩分類問題(在此基礎上衍生出來的softmax可以用于多分類),且必須線性可分;
對于非線性特征,需要進行轉換;
3.線性回歸
線性回歸是用于回歸的,而不像Logistic回歸是用于分類,其基本思想是用梯度下降法對最小二乘法形式的誤差函數進行優化,當然也可以用normal equation直接求得參數的解,結果為:
而在LWLR(局部加權線性回歸)中,參數的計算表達式為:
由此可見LWLR與LR不同,LWLR是一個非參數模型,因為每次進行回歸計算都要遍歷訓練樣本至少一次。
優點: 實現簡單,計算簡單;
缺點: 不能擬合非線性數據.
4.最近鄰算法——KNN
KNN即最近鄰算法,其主要過程為:
1. 計算訓練樣本和測試樣本中每個樣本點的距離(常見的距離度量有歐式距離,馬氏距離等); 2. 對上面所有的距離值進行排序; 3. 選前k個最小距離的樣本; 4. 根據這k個樣本的標簽進行投票,得到最后的分類類別;?
如何選擇一個最佳的K值,這取決于數據。一般情況下,在分類時較大的K值能夠減小噪聲的影響。但會使類別之間的界限變得模糊。一個較好的K值可通過各種啟發式技術來獲取,比如,交叉驗證。另外噪聲和非相關性特征向量的存在會使K近鄰算法的準確性減小。
近鄰算法具有較強的一致性結果。隨著數據趨于無限,算法保證錯誤率不會超過貝葉斯算法錯誤率的兩倍。對于一些好的K值,K近鄰保證錯誤率不會超過貝葉斯理論誤差率。
KNN算法的優點
理論成熟,思想簡單,既可以用來做分類也可以用來做回歸;
可用于非線性分類;
訓練時間復雜度為O(n);
對數據沒有假設,準確度高,對outlier不敏感;
缺點
計算量大;
樣本不平衡問題(即有些類別的樣本數量很多,而其它樣本的數量很少);
需要大量的內存;
5.決策樹
易于解釋。它可以毫無壓力地處理特征間的交互關系并且是非參數化的,因此你不必擔心異常值或者數據是否線性可分(舉個例子,決策樹能輕松處理好類別A在某個特征維度x的末端,類別B在中間,然后類別A又出現在特征維度x前端的情況)。它的缺點之一就是不支持在線學習,于是在新樣本到來后,決策樹需要全部重建。另一個缺點就是容易出現過擬合,但這也就是諸如隨機森林RF(或提升樹boosted tree)之類的集成方法的切入點。另外,隨機森林經常是很多分類問題的贏家(通常比支持向量機好上那么一丁點),它訓練快速并且可調,同時你無須擔心要像支持向量機那樣調一大堆參數,所以在以前都一直很受歡迎。
決策樹中很重要的一點就是選擇一個屬性進行分枝,因此要注意一下信息增益的計算公式,并深入理解它。
信息熵的計算公式如下:
其中的n代表有n個分類類別(比如假設是2類問題,那么n=2)。分別計算這2類樣本在總樣本中出現的概率p1和p2,這樣就可以計算出未選中屬性分枝前的信息熵。
現在選中一個屬性$x_i$用來進行分枝,此時分枝規則是:如果$x_i=v$的話,將樣本分到樹的一個分支;如果不相等則進入另一個分支。很顯然,分支中的樣本很有可能包括2個類別,分別計算這2個分支的熵H1和H2,計算出分枝后的總信息熵H’ =p1 ?H1+p2 ?H2,則此時的信息增益ΔH = H - H’。以信息增益為原則,把所有的屬性都測試一邊,選擇一個使增益最大的屬性作為本次分枝屬性。
決策樹自身的優點
計算簡單,易于理解,可解釋性強;
比較適合處理有缺失屬性的樣本;
能夠處理不相關的特征;
在相對短的時間內能夠對大型數據源做出可行且效果良好的結果。
缺點
容易發生過擬合(隨機森林可以很大程度上減少過擬合);
忽略了數據之間的相關性;
對于那些各類別樣本數量不一致的數據,在決策樹當中,信息增益的結果偏向于那些具有更多數值的特征(只要是使用了信息增益,都有這個缺點,如RF)。
5.1 Adaboosting
Adaboost是一種加和模型,每個模型都是基于上一次模型的錯誤率來建立的,過分關注分錯的樣本,而對正確分類的樣本減少關注度,逐次迭代之后,可以得到一個相對較好的模型。是一種典型的boosting算法。下面是總結下它的優缺點。
優點
adaboost是一種有很高精度的分類器。
可以使用各種方法構建子分類器,Adaboost算法提供的是框架。
當使用簡單分類器時,計算出的結果是可以理解的,并且弱分類器的構造極其簡單。
簡單,不用做特征篩選。
不容易發生overfitting。
關于隨機森林和GBDT等組合算法,參考這篇文章:機器學習-組合算法總結
缺點:對outlier比較敏感
5.2 xgboost
這是一個近年來出現在各大比賽的大殺器,奪冠選手很大部分都使用了它。
高準確率高效率高并發,支持自定義損失函數,既可以用來分類又可以用來回歸
可以像隨機森林一樣輸出特征重要性,因為速度快,適合作為高維特征選擇的一大利器
在目標函數中加入正則項,控制了模型的復雜程度,可以避免過擬合
支持列抽樣,也就是隨機選擇特征,增強了模型的穩定性
對缺失值不敏感,可以學習到包含缺失值的特征的分裂方向
另外一個廣受歡迎的原因是支持并行,速度杠杠的
用的好,你會發現他的全部都是優點
6.SVM支持向量機
高準確率,為避免過擬合提供了很好的理論保證,而且就算數據在原特征空間線性不可分,只要給個合適的核函數,它就能運行得很好。在動輒超高維的文本分類問題中特別受歡迎。可惜內存消耗大,難以解釋,運行和調參也有些煩人,而隨機森林卻剛好避開了這些缺點,比較實用。
優點
可以解決高維問題,即大型特征空間;
能夠處理非線性特征的相互作用;
無需依賴整個數據;
可以提高泛化能力;
需要對數據提前歸一化,很多人使用的時候忽略了這一點,畢竟是基于距離的模型,所以LR也需要歸一化
缺點
當觀測樣本很多時,效率并不是很高;
一個可行的解決辦法是模仿隨機森林,對數據分解,訓練多個模型,然后求平均,時間復雜度降低p倍,分多少份,降多少倍
對非線性問題沒有通用解決方案,有時候很難找到一個合適的核函數;
對缺失數據敏感;
對于核的選擇也是有技巧的(libsvm中自帶了四種核函數:線性核、多項式核、RBF以及sigmoid核):
第一,如果樣本數量小于特征數,那么就沒必要選擇非線性核,簡單的使用線性核就可以了;
第二,如果樣本數量大于特征數目,這時可以使用非線性核,將樣本映射到更高維度,一般可以得到更好的結果;
第三,如果樣本數目和特征數目相等,該情況可以使用非線性核,原理和第二種一樣。
對于第一種情況,也可以先對數據進行降維,然后使用非線性核,這也是一種方法。
7. 人工神經網絡的優缺點
人工神經網絡的優點:
分類的準確度高;
并行分布處理能力強,分布存儲及學習能力強,
對噪聲神經有較強的魯棒性和容錯能力,能充分逼近復雜的非線性關系;
具備聯想記憶的功能。
人工神經網絡的缺點:
神經網絡需要大量的參數,如網絡拓撲結構、權值和閾值的初始值;
不能觀察之間的學習過程,輸出結果難以解釋,會影響到結果的可信度和可接受程度;
學習時間過長,甚至可能達不到學習的目的。
8、K-Means聚類
關于K-Means聚類的文章,鏈接:機器學習算法-K-means聚類。關于K-Means的推導,里面有著很強大的EM思想。
優點
算法簡單,容易實現 ;
對處理大數據集,該算法是相對可伸縮的和高效率的,因為它的復雜度大約是O(nkt),其中n是所有對象的數目,k是簇的數目,t是迭代的次數。通常k<<n。這個算法通常局部收斂。
算法嘗試找出使平方誤差函數值最小的k個劃分。當簇是密集的、球狀或團狀的,且簇與簇之間區別明顯時,聚類效果較好。
缺點
對數據類型要求較高,適合數值型數據;
可能收斂到局部最小值,在大規模數據上收斂較慢
K值比較難以選取;
對初值的簇心值敏感,對于不同的初始值,可能會導致不同的聚類結果;
不適合于發現非凸面形狀的簇,或者大小差別很大的簇。
對于”噪聲”和孤立點數據敏感,少量的該類數據能夠對平均值產生極大影響。
算法選擇參考
之前翻譯過一些國外的文章,有一篇文章中給出了一個簡單的算法選擇技巧:
首當其沖應該選擇的就是邏輯回歸,如果它的效果不怎么樣,那么可以將它的結果作為基準來參考,在基礎上與其他算法進行比較;
然后試試決策樹(隨機森林)看看是否可以大幅度提升你的模型性能。即便最后你并沒有把它當做為最終模型,你也可以使用隨機森林來移除噪聲變量,做特征選擇;
如果特征的數量和觀測樣本特別多,那么當資源和時間充足時(這個前提很重要),使用SVM不失為一種選擇。
通常情況下:【XGBOOST>=GBDT>=SVM>=RF>=Adaboost>=Other…】,現在深度學習很熱門,很多領域都用到,它是以神經網絡為基礎的,目前我自己也在學習,只是理論知識不是很厚實,理解的不夠深,這里就不做介紹了。
算法固然重要,但好的數據卻要優于好的算法,設計優良特征是大有裨益的。假如你有一個超大數據集,那么無論你使用哪種算法可能對分類性能都沒太大影響(此時就可以根據速度和易用性來進行抉擇)。
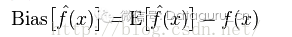
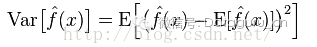
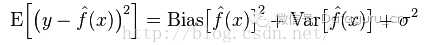
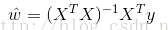
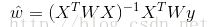
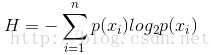





![luogu P3244 [HNOI2015]落憶楓音](http://pic.xiahunao.cn/luogu P3244 [HNOI2015]落憶楓音)




是什么鬼)








