例子一:
理論:
簡版:猜(E-step),反思(M-step),重復;
啰嗦版:
你知道一些東西(觀察的到的數據), 你不知道一些東西(觀察不到的),你很好奇,想知道點那些不了解的東西。怎么辦呢,你就根據一些假設(parameter)先猜(E-step),把那些不知道的東西都猜出來,假裝你全都知道了; 然后有了這些猜出來的數據,你反思一下,更新一下你的假設(parameter), 讓你觀察到的數據更加可能(Maximize likelihood; M-stemp); 然后再猜,在反思,最后,你就得到了一個可以解釋整個數據的假設了。
1. 注意,你猜的時候,要盡可能的猜遍所有情況,然后求期望(Expected);就是你不能僅僅猜一個個例,而是要猜出來整個宇宙;
2. 為什么要猜,因為反思的時候,知道全部的東西比較好。(就是P(X,Z)要比P(X)好優化一些。Z是hidden states)
3. 最后你得到什么了?你得到了一個可以解釋數據的假設,可能有好多假設都能解釋數據,可能別的假設更好。不過沒關系,有總比沒有強,知足吧。(你陷入到local minimum了)
====
實踐:
背景:公司有很多領導=[A總,劉總,C總],同時有很多漂亮的女職員=[小甲,小章,小乙]。(請勿對號入座)你迫切的懷疑這些老總跟這些女職員有問題。為了科學的驗證你的猜想,你進行了細致的觀察。于是,
觀察數據:
1)A總,小甲,小乙一起出門了;
2)劉總,小甲,小章一起出門了;
3)劉總,小章,小乙一起出門了;
4)C總,小乙一起出門了;
收集到了數據,你開始了神秘的EM計算:
初始化,你覺得三個老總一樣帥,一樣有錢,三個美女一樣漂亮,每個人都可能跟每個人有關系。所以,每個老總跟每個女職員“有問題”的概率都是1/3;
這樣,(E step)
1) A總跟小甲出去過了 1/2 * 1/3 = 1/6 次,跟小乙也出去了1/6次;(所謂的fractional count)
2)劉總跟小甲,小章也都出去了1/6次
3)劉總跟小乙,小章又出去了1/6次
4)C總跟小乙出去了1/3次
總計,A總跟小甲出去了1/6次,跟小乙也出去了1/6次 ; 劉總跟小甲,小乙出去了1/6次,跟小章出去了1/3次;C總跟小章出去了1/3次;
你開始跟新你的八卦了(M step),
A總跟小甲,小乙有問題的概率都是1/6 / (1/6 + 1/6) = 1/2;
劉總跟小甲,小乙有問題的概率是1/6 / (1/6+1/6+1/6+1/6) = 1/4; 跟小章有問題的概率是(1/6+1/6)/(1/6 * 4) = 1/2;
C總跟小乙有問題的概率是 1。
然后,你有開始根據最新的概率計算了;(E-step)
1)A總跟小甲出去了 1/2 * 1/2 = 1/4 次,跟小乙也出去 1/4 次;
2)劉總跟小甲出去了1/2 * 1/4 = 1/12 次, 跟小章出去了 1/2 * 1/2 = 1/4 次;
3)劉總跟小乙出去了1/2 * 1/4 = 1/12 次, 跟小章又出去了 1/2 * 1/2 = 1/4 次;
4)C總跟小乙出去了1次;
重新反思你的八卦(M-step):
A總跟小甲,小乙有問題的概率都是1/4/ (1/4 + 1/4) = 1/2;
B總跟小甲,小乙是 1/12 / (1/12 + 1/4 + 1/4 + 1/12) = 1/8 ; 跟小章是 3/4 ;
C總跟小乙的概率是1。
你繼續計算,反思,總之,最后,你得到了真相!(馬總表示我早就知道真相了)
你知道了這些老總的真相,可以開始學習機器翻譯了。現在一個班里有50個男生,50個女生,且男生站左,女生站右。我們假定男生的身高服從正態分布 ,女生的身高則服從另一個正態分布:
。這時候我們可以用極大似然法(MLE),分別通過這50個男生和50個女生的樣本來估計這兩個正態分布的參數。
但現在我們讓情況復雜一點,就是這50個男生和50個女生混在一起了。我們擁有100個人的身高數據,卻不知道這100個人每一個是男生還是女生。
這時候情況就有點尷尬,因為通常來說,我們只有知道了精確的男女身高的正態分布參數我們才能知道每一個人更有可能是男生還是女生。但從另一方面去考量,我們只有知道了每個人是男生還是女生才能盡可能準確地估計男女各自身高的正態分布的參數。
這個時候有人就想到我們必須從某一點開始,并用迭代的辦法去解決這個問題:我們先設定男生身高和女生身高分布的幾個參數(初始值),然后根據這些參數去判斷每一個樣本(人)是男生還是女生,之后根據標注后的樣本再反過來重新估計參數。之后再多次重復這個過程,直至穩定。這個算法也就是EM算法。
案例三
鏈接:https://www.zhihu.com/question/40797593/answer/275171156
來源:知乎
著作權歸作者所有。商業轉載請聯系作者獲得授權,非商業轉載請注明出處。
第一層境界, EM算法就是E 期望 + M 最大化
最經典的例子就是拋3個硬幣,跑I硬幣決定C1和C2,然后拋C1或者C2決定正反面, 然后估算3個硬幣的正反面概率值。
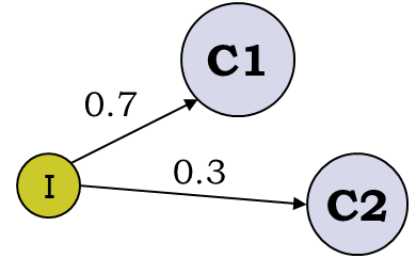
這個例子為什么經典, 因為它告訴我們,當存在隱變量I的時候, 直接的最大似然估計無法直接搞定。 什么是隱變量?為什么要引入隱變量? 對隱變量的理解是理解EM算法的第一要義!Chuong B Do & Serafim Batzoglou的Tutorial論文“What is the expectation maximization algorithm?”對此有詳細的例子進行分析。
a
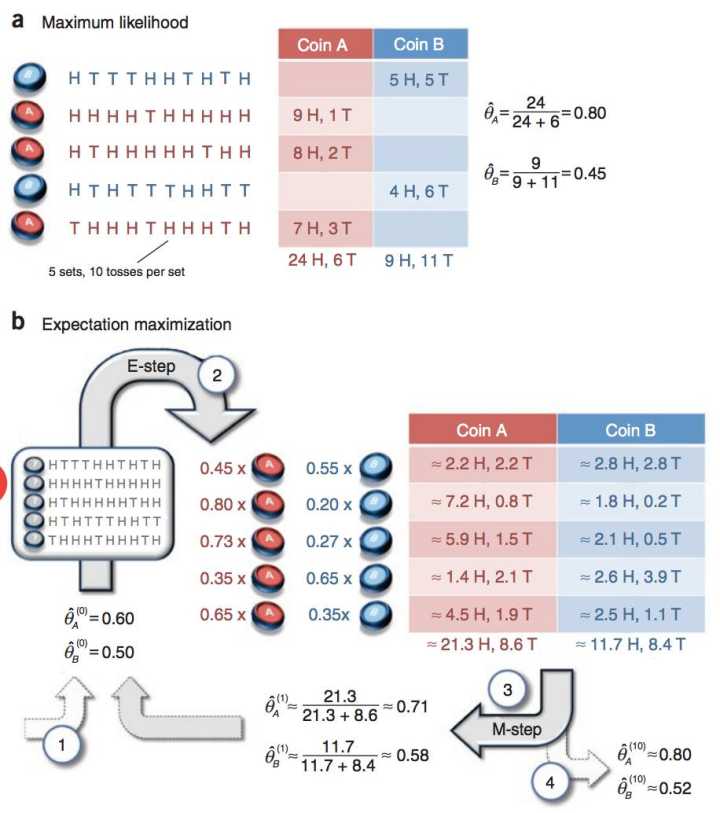
?這是一個拋硬幣的例子,H表示正面向上,T表示反面向上,參數θ表示正面朝上的概率。硬幣有兩個,A和B,硬幣是有偏的。本次實驗總共做了5組,每組隨機選一個硬幣,連續拋10次。如果知道每次拋的是哪個硬幣,那么計算參數θ就非常簡單了,如上圖所示。
???????? 如果不知道每次拋的是哪個硬幣呢?那么,我們就需要用EM算法,基本步驟為:1、給θA和θB一個初始值;2、(E-step)估計每組實驗是硬幣A的概率(本組實驗是硬幣B的概率=1-本組實驗是硬幣A的概率)。分別計算每組實驗中,選擇A硬幣且正面朝上次數的期望值,選擇B硬幣且正面朝上次數的期望值;3、(M-step)利用第三步求得的期望值重新計算θA和θB;4、當迭代到一定次數,或者算法收斂到一定精度,結束算法,否則,回到第2步。
b
?稍微解釋一下上圖的計算過程。初始值θA=0.6,θB=0.5。
????????圖中的0.45是怎么得來的呢?由兩個硬幣的初始值0.6和0.5,容易得出投擲出5正5反的概率是pA=C(10,5)*(0.6^5)*(0.4^5),pB=C(10,5)*(0.5^5)*(0.5^5), ?pA/(pA+pB)=0.449, ?0.45就是0.449近似而來的,表示第一組實驗選擇的硬幣是A的概率為0.45。圖中的2.2H,2.2T是怎么得來的呢? ?0.449 * 5H = 2.2H ,0.449 * 5T = 2.2T ,表示第一組實驗選擇A硬幣且正面朝上次數的期望值是2.2。其他的值依次類推。
通過隱變量,我們第一次解讀了EM算法的偉大!突破了直接MLE的限制(不詳細解釋了)。

至此, 你理解了EM算法的第一層境界,看山是山。?



是什么鬼)















