鏈接:https://www.zhihu.com/question/26665048/answer/157852228
來源:知乎
著作權歸作者所有。商業轉載請聯系作者獲得授權,非商業轉載請注明出處。
馬爾可夫鏈 (Markov Chain)是什么鬼
它是隨機過程中的一種過程,一個統計模型,到底是哪一種過程呢?好像一兩句話也說不清楚,還是先看個例子吧。
先說說我們村智商為0的王二狗,人傻不拉幾的,見人就傻笑,每天中午12點的標配,仨狀態:吃,玩,睡。這就是傳說中的狀態分布。

你想知道他n天后中午12點的狀態么?是在吃,還是在玩,還是在睡?這些狀態發生的概率分別都是多少? (知道你不想,就假裝想知道吧~~學習真的好累~~)
先看個假設,他每個狀態的轉移都是有概率的,比如今天玩,明天睡的概率是幾,今天玩,明天也玩的概率是幾幾,還是先看個圖吧,更直觀一些。

這個矩陣就是轉移概率矩陣P,并且它是保持不變的,就是說第一天到第二天的轉移概率矩陣跟第二天到第三天的轉移概率矩陣是一樣的。(這個叫時齊,不細說了,有興趣的同學自行百度)。
有了這個矩陣,再加上已知的第一天的狀態分布,就可以計算出第N天的狀態分布了。

S1 是4月1號中午12點的的狀態分布矩陣 [0.6, 0.2, 0.2],里面的數字分別代表吃的概率,玩的概率,睡的概率。
那么
4月2號的狀態分布矩陣 S2 = S1 * P (倆矩陣相乘)。
4月3號的狀態分布矩陣 S3 = S2 * P (看見沒,跟S1無關,只跟S2有關)。
4月4號的狀態分布矩陣 S4 = S3 * P (看見沒,跟S1,S2無關,只跟S3有關)。
...
4月n號的狀態分布矩陣 Sn = Sn-1 * P (看見沒,只跟它前面一個狀態Sn-1有關)。
-------------------------------------------------------------------------------------------------------------------------
總結:馬爾可夫鏈就是這樣一個任性的過程,它將來的狀態分布只取決于現在,跟過去無關!
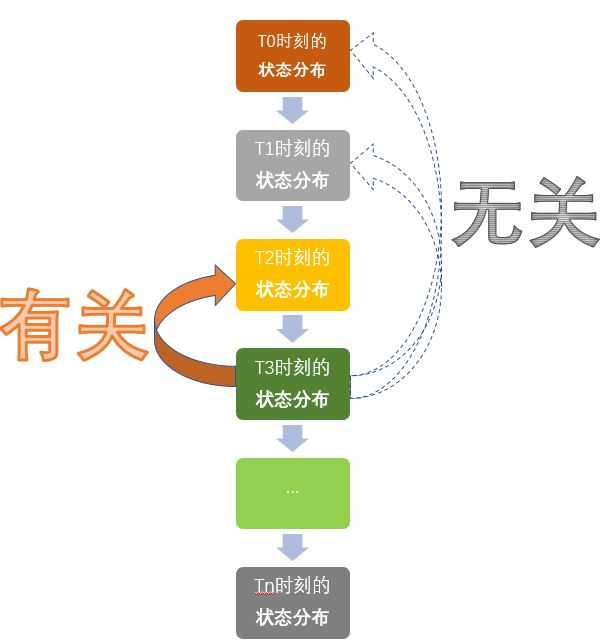
就把下面這幅圖想象成是一個馬爾可夫鏈吧。實際上就是一個隨機變量隨時間按照Markov性質進行變化的過程。
-----------------------------更新-------------------------------
有人問到 S2 的計算過程,那我就貼上來吧,不關心的同學可以忽略。
這是我手寫的計算過程。
科學中的應用
馬爾可夫鏈通常用來建模排隊理論和統計學中的建模,還可作為信號模型用于熵編碼技術,如算法編碼。馬爾可夫鏈也有眾多的生物學應用,特別是人口過程,可以幫助模擬生物人口過程的建模。隱蔽馬爾可夫模型還被用于生物信息學,用以編碼區域或基因預測。
馬爾可夫鏈最近的應用是在地理統計學(geostatistics)中。其中,馬爾可夫鏈用在基于觀察數據的二到三維離散變量的隨機模擬。這一應用類似于“克里金”地理統計學(Kriging geostatistics),被稱為是“馬爾可夫鏈地理統計學”。這一馬爾可夫鏈地理統計學方法仍在發展過程中。
馬爾可夫鏈模型主要是分析一個人在某一階段內由一個職位調到另一個職位的可能性,即調動的概率。該模型的一個基本假設就是,過去的內部人事變動的模式和概率與未來的趨勢大體相一致。實際上,這種方法是要分析企業內部人力資源的流動趨勢和概率,如升遷、轉職、調配或離職等方面的情況,以便為內部的人力資源的調配提供依據。
它的基本思想是:通過發現過去組織人事變動的規律,以推測組織在未來人員的供給情況。馬爾可夫鏈模型通常是分幾個時期收集數據,然后再得出平均值,用這些數據代表每一種職位中人員變動的頻率,就可以推測出人員變動情況。
具體做法是:將計劃初期每一種工作的人數量與每一種工作的人員變動概率相乘,然后縱向相加,即得到組織內部未來勞動力的凈供給量。其基本表達式為:
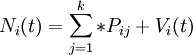
- Ni(t):t時間內I類人員數量;
- Pji:人員從j類向I類轉移的轉移率;
- Vi(t):在時間(t-1,t)I類所補充的人員數。
企業人員的變動有調出、調入、平調、晉升與降級五種。表3 假設一家零售公司在1999至2000年間各類人員的變動情況。年初商店經理有12人,在當年期間平均90%的商店經理仍在商店內,10%的商店經理離職,期初36位經理助理有 11%晉升到經理,83%留在原來的職務,6%離職;如果人員的變動頻率是相對穩定的,那么在2000年留在經理職位上有11人(12×90%),另外,經理助理中有4人(36×83%)晉升到經理職位,最后經理的總數是15人(11+4)。可以根據這一矩陣得到其他人員的供給情況,也可以計算出其后各個時期的預測結果。假設的零售公司的馬爾可夫分析,見下表:
| 1999~2000 | 商店經理 | 經理助理 | 區域經理 | 部門經理 | 銷售員 | 離職 |
|---|---|---|---|---|---|---|
| 商店經理 (n=12) | 90% 11 | ? | ? | ? | ? | 10% 1 |
| 經理助理 (n=36) | 11% 4 | 83% 30 | ? | ? | ? | 6% 2 |
| 區域經理 (n=96) | ? | 11% 11 | 66% 63 | 8% 8 | ? | 15% 14 |
| 部門經理 (=288) | ? | ? | 10% 29 | 72% 207 | 2% 6 | 16% 46 |
| 銷售員 (=1440) | ? | ? | ? | 6% 86 | 74% 1066 | 25% 228 |
| 供給預測 | 15 | 41 | 92 | 301 | 1072 | 351 |