第十章內部排序
10.1 概述
排序就是把一組數據按關鍵字的大小有規律地排列。經過排序的數據更易于查找。
?
排序前Ki=Kj,且Ki在前:
排序方法是穩定的,若排序后Ki在前;
排序方法是不穩定的,如排序后Kj在前。
?
分類:
內部排序:排序過程在內存中進行;
外部排序:待排序記錄的數量很大,內存一次不能容納全部記錄,需要對外存進行訪問。
?
內部排序每一種方法都有各自的優缺點,適合在不同的環境下使用。
?
按不同原則進行分類:
插入排序 ? ?直接插入排序 ?其他插入排序 ?希爾排序
交換排序 ? ?冒泡 快速排序
選擇排序 ? ?簡單選擇排序 ?樹形選擇排序 ?堆排序
歸并排序 ? ?
基數排序
?
按時間復雜度劃分:
簡單排序方法 ?n^2
先進排序方法 ?nlogn
基數排序方法 ?d*n
?
10.2 插入排序
10.2.1 直接插入排序
直接插入排序(Straight Insertion Sort) ?n^2
基本操作是將一個記錄插入到已排好序的有序表中,從而得到一個新的、記錄數增一的有序表。
哨兵在0號位置,值為待插入數據。
?
10.2.2 其他插入排序
當待排序記錄的數量n很小時,插入排序是一種很好的排序方法。
插入排序的改進:從減少“比較”和“移動”這兩種操作的次數出發。
1.?折半插入排序(Binary Insertion Sort) ?n^2
由于插入排序的基本操作是在一個有序表中進行查找和插入,這個查找操作可利用折半查找來實現。
減少了比較次數,移動次數不變。 ?
2. 2-路插入排序
在折半插入的基礎上再改進之,其目的是減少排序過程中移動記錄的次數,但需要n個記錄的輔助空間。
移動次數約為(n^2)/8。
若L.r[1]是最小或最大,則2-路插入排序就失去其優越性。
循環數組:+1 mod length ???-1 plus length mod length
?
10.2.3 希爾排序 ?n^1.3 ?
希爾排序(Shell’s Sort)又稱“縮小增量排序”(Diminishing Increment Sort)
一種插入排序類方法,但在時間效率上較前述排序方法有較大的改進。
基本思想:
先將整個待排記錄序列分割成若干子序列分別進行直接插入排序,待整個序列中的記錄“基本有序”時,再對全體記錄進行一次直接插入排序。
子序列的構成不是簡單的“逐段分割”,而是將相隔某個“增量”的記錄組成一個子序列。
?
由于在前幾趟的插入排序中記錄的關鍵字是和同一子序列中的前一個記錄的關鍵字進行比較,因此關鍵字較小的記錄不是一步一步地向前挪動,而是跳躍式地往前移,從而使得在最后一趟增量為1的插入排序時,序列已基本有序,只要作記錄的少量比較和移動即可完成排序,因此希爾排序的時間復雜度較直接插入排序低。??
增量序列中的值只有公因子1,并且最后一個增量值必須等于1。
?
10.3 快速排序
基于交換
起泡排序(Bubble Sort)
快速排序(Quick Sort)
基本思想:
通過一趟排序將待排序記錄分割成獨立的兩部分,其中一部分記錄的關鍵字均比另一部分記錄的關鍵字小,然后分別對這兩部分記錄繼續進行排序,已達到整個序列有序。
快速排序被認為是,在所有同數量級(nlogn)的排序方法中,其平均性能最好。
?
10.4 選擇排序(Selection Sort)
10.4.1 簡單選擇排序(Simple Selection Sort)
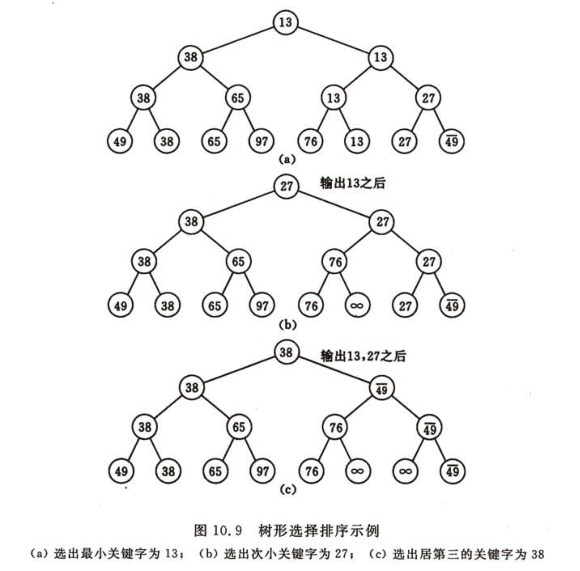
10.4.2 樹形選擇排序(Tree Selection Sort)
又稱錦標賽排序(Tournament Sort)
完全二叉樹的層數
n個葉子結點的完全二叉樹,葉子結點表示關鍵字,非葉子結點中的關鍵字等于左右孩子結點中較小的關鍵字,根結點為最小關鍵字。
將最小關鍵字置為“最大值”,然后從該葉子結點開始,和其兄弟結點進行比較,可選出次最小關鍵字。
依此類推。
缺點:輔助存儲空間較多,和“最大值”進行多余比較。
?
10.4.3 堆排序(Heap Sort)
只需要一個記錄大小的輔助空間,每個待排序的記錄僅占有一個存儲空間。
堆:n個元素的序列{K1, K2, ..., Kn}當且僅當滿足以下關系時,稱之為堆。
若將和此序列對應的一維數組看成是一個完全二叉樹,則堆的含義表明,完全二叉樹中所有非終端結點的值均不小于其左右孩子結點的值(大頂堆)。由此,堆頂元素必為序列中n個元素的最大值。
?
若在輸出堆頂的最大值后,使得剩余n-1個元素的序列又建成一個堆,則得到n個元素的次大值。如此反復執行,便能能得到一個有序序列,這個過程稱之為堆排序。
?
問題一:如何在輸出堆頂元素之后,調整剩余元素成為一個新堆?
輸出堆頂元素后,以堆中最后一個元素代替之。
此時根結點的左右子樹均為堆,則僅需自上而下進行調整即可。
稱自堆頂至葉子的調整過程為“篩選”。
問題二:如何由一個無序序列建成一個堆?
從一個無序序列建堆的過程就是一個反復“篩選”的過程。
若將此序列看成一個完全二叉樹,則最后一個非終端結點是第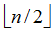
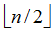
?
堆排序方法對記錄數較少的文件并不值得提倡,但對n較大的文件還是很有效的。
其運行時間主要耗費在建初始堆和調整建新堆時進行的反復“篩選”上。
?
堆排序在最壞的情況下,其時間復雜度也為nlogn。相對于快速排序來說,這是堆排序的最大優點。此外,堆排序僅需一個記錄大小供交換用的輔助存儲空間。
?
?
10.5 歸并排序(Merging Sort)
“歸并”的含義是將兩個或兩個以上的有序表組成一個新的有序表。
實現歸并排序需和待排記錄等數量的輔助空間,其時間復雜度為nlogn。
遞歸形式的算法在形式上較簡潔,但實用性很差。
與快速排序和堆排序相比,歸并排序最大的特點是,它是一種穩定的排序算法。
但在一般情況下,很少使用二路歸并排序法進行內部排序。
?
?
10.6 基數排序(Radix Sorting)
基數排序是一種借助多關鍵字排序的思想對單邏輯關鍵字進行排序的方法。
最高位優先(Most Significant Digit first)MSD
最低位優先(Least Significant Digit first)LSD
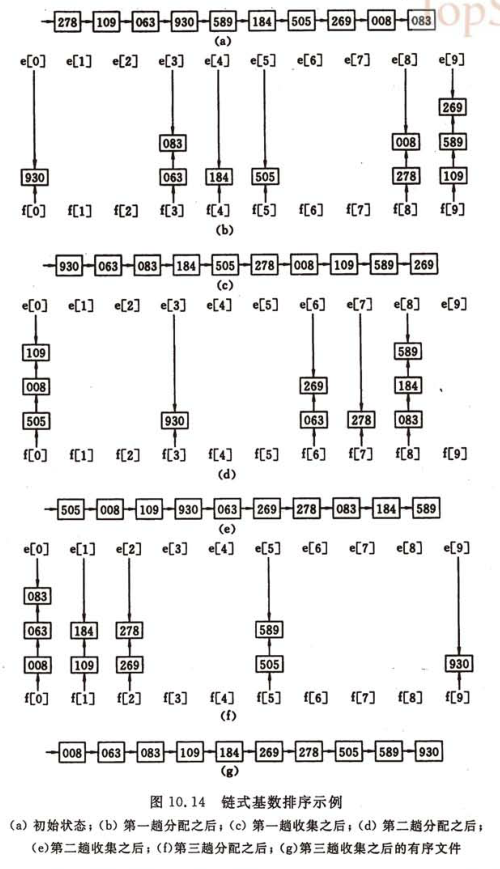
鏈式基數排序
借助“分配”和“收集”兩種操作對單邏輯關鍵字進行排序的一種內部排序方法。
?
首先,以靜態鏈表存儲n個待排記錄,并令表頭指針指向第一個記錄。
第一趟分配對最低位數的關鍵字進行,將鏈表中的記錄分配至Radix個鏈隊列中去,f[i] e[i]分別指向第i個隊列的頭指針和尾指針。
第一趟收集是將Radix個鏈隊列串為一個鏈隊列。
然后進行第二趟分配、第二趟收集、第三趟分配、第三趟收集、...
10.7 各種內部排序方法的比較
| 排序方法 | 平均時間 | 最壞情況 | 輔助存儲 |
| 簡單排序 | n^2 | n^2 | 1 |
| 快速排序 | nlogn | n^2 | logn |
| 堆排序 | nlogn | nlogn | 1 |
| 歸并排序 | nlogn | nlogn | n |
| 基數排序 | d*n | d*n | rd |
?
(1)從平均性能而言,快速排序最佳,其所需時間最省,但快速排序在最壞情況下的時間性能不如堆排序和歸并排序。
(2)在n較大時,歸并排序所需時間較堆排序少,但它所需的輔助存儲變量最多。
(3)直接插入排序最簡單,當基本有序或n值較小時,它是最佳的排序方法,因此常將其和其他排序方法,諸如快速排序、歸并排序等結合在一起使用。
(4)基數排序適用于n很大,而關鍵字“位數”較小的序列。
(5)基數排序是穩定的內排方法。所有時間復雜度為O(n^2)的簡單排序法也是穩定的。
快速排序、堆排序、希爾排序是不穩定的。
?
綜上所述,沒有哪一種排序方法是絕對最優的,在實際應用時根據不同情況適當選用,甚至可將多種方法結合起來使用。
??
“地址排序”:另設一個地址向量指示相應記錄;同時在排序過程中不移動記錄而移動地址向量中相應分量的內容。


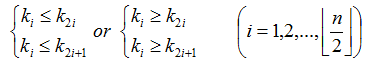


![[Objective-C語言教程]結構體(17)](http://pic.xiahunao.cn/[Objective-C語言教程]結構體(17))







——單例模式)








