首先看一下reduce_sum及其參數的注釋 :

def tf.reduce_sum(input_tensor, axis=None, keepdims=False, name=None)

Computes the sum of elements across dimensions of a tensor.

Reduces input_tensor along the dimensions given in axis. Unless keepdims is true, the rank of the tensor is reduced by 1 for each entry in axis. If keepdims is true, the reduced dimensions are retained with length 1.

If axis is None, all dimensions are reduced, and a tensor with a
single element is returned.

1 參數只有一個矩陣 input_tensor，其余參數為默認

下面我們用三個張量為例(下統一稱為矩陣)，對一維向量，二維矩陣，三維矩陣分別執行其余參數為默認的reduce_sum()運算。

x_dim_1 = tf.constant([1,2,3])
z = tf.reduce_sum(x_dim_1)
print("1D sum :")
print(z)x_dim_2 = tf.constant([[1,2,3],[4,5,6]])
z = tf.reduce_sum(x_dim_2)
print("2D sum :")
print(z)x_dim_3 = tf.constant([[[1,2],[2,3],[3,4]],[[4,5],[5,6],[6,7]]])z = tf.reduce_sum(x_dim_3)
print("3D sum :")
print(z)

輸出結果如下:

不難看出，無論是對幾維矩陣而言，tf.reduce_sum()方法均對矩陣的所有元素進行求和，并將結果降維至一維，返回一個數值(0維矩陣)。 在這種情況下，tf.reduce_sum()方法與我們熟悉的numpy.sum()方法可以說在矩陣運算方面別無二致，同時也符合注釋中所說 :

If axis is None, all dimensions are reduced, and a tensor with a
single element is returned.

2 保持keepdims參數為false，改變axis參數的值進行運算

這個部分就是reduce_sum的靈魂所在，其關鍵是要理解所謂axis參數對于高維矩陣的意義。
不妨先看看，如果我們打印出上述代碼中的三個矩陣常量的shape，會得到什么:

需要理解的是，對于高維矩陣來說，其每一個元素都是一個低維矩陣。 例如，對于一維矩陣(數組) x_dim_1 而言，每一個元素都是一個0維的數組(數值) : 1，2，3。 對于高維矩陣，以三維矩陣x_dim_3 為例，其每一個元素都是一個二維的矩陣，這些二維矩陣中的每一個元素都是一個一維數組，這些一維數組中的每個元素都是一個0維矩陣(數值)。

聽起來好像像繞口令，那么我們就以x_dim_3為例，具體解釋axis與矩陣的shape之間的關系。
x_dim_3 = [ [ [1,2],[2,3],[3,4] ],
[ [4,5],[5,6],[6,7] ] ]

首先我們不難看出，這是一個三維矩陣。那么該矩陣包含了幾個二維矩陣的元素呢，我們不難看出包含了兩個，分別是 [ [1,2],[2,3],[3,4] ] 以及 [ [4,5],[5,6],[6,7] ] 兩個二維矩陣。那么對于每一個作為元素的二維矩陣，又包含了多少個一維數組呢，顯然，每一個二維矩陣都包含了三個一維數組。以第一個二維數組元素為例，包含了[1,2],[2,3],[3,4]三個一維數組元素。而每一個一維數組元素，又分別包含了兩個0維數組(數值)。

這就是張量 x_dim_3 的shape的構成(2,3,2)，其代表的數學意義為，這個三維矩陣包含了兩個二維矩陣元素，每一個二維矩陣又包含了三個一維矩陣元素，每一個一維矩陣又包含了兩個數值。同時，三個數值分別對應了axis=0 axis=1 axis=2 三個軸分別包含的元素個數。

問題實際變成了，沿著axis=0 : 對包含的兩個二維矩陣元素進行求和， 沿著axis=1 : 對該維度包含的三個一維矩陣進行求和，沿著axis = 2 : 對該維度包含的兩個數值進行求和。 下面放出對x_dim_3的測試及輸出結果。

# 沿著axis = 0 對三維矩陣進行降維求和 實際就是對兩個二維矩陣元素進行加法運算
x_dim_3 = tf.constant([[[1,2],[2,3],[3,4]],[[4,5],[5,6],[6,7]]])
z = tf.reduce_sum(x_dim_3,axis=0)
print(z)

輸出結果如下:

注釋 :

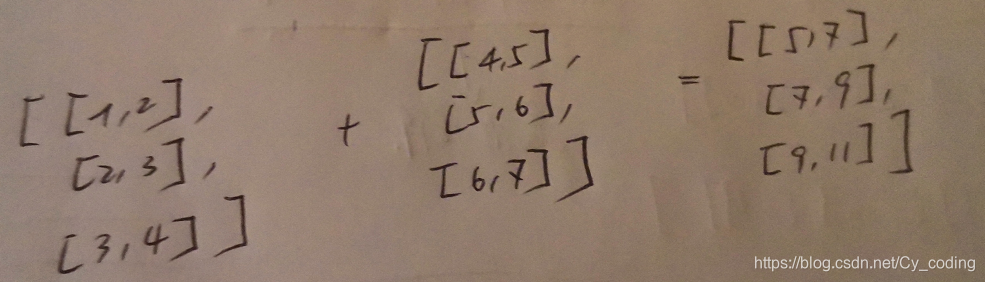
# 沿著axis=1 對三維矩陣進行降維求和 
x_dim_3 = tf.constant([[[1,2],[2,3],[3,4]],[[4,5],[5,6],[6,7]]])
z = tf.reduce_sum(x_dim_3,axis=1)
print(z)

# 沿著axis=2對三維矩陣進行降維求和 
x_dim_3 = tf.constant([[[1,2],[2,3],[3,4]],[[4,5],[5,6],[6,7]]])
z = tf.reduce_sum(x_dim_3,axis=2)
print(z)

3 總結

reduce_sum方法人如其名，減少維度的同時對矩陣內部沿著某一軸進行求和。與之類似的方法還有reduce_max, reduce_min, reduce_mean,他們關于axis參數的使用與本篇文章中分析的是別無二致的。當然，axis可以不是一個數值，而是一個矩陣，有興趣的可以進一步探索與發現。