計算被直線劃分區域

在笛卡爾坐標系，存在區域[A,B],被不同線劃分成多塊小的區域，簡單起見，假設這些不同線都直線并且不存在三條直線相交于一點的情況。

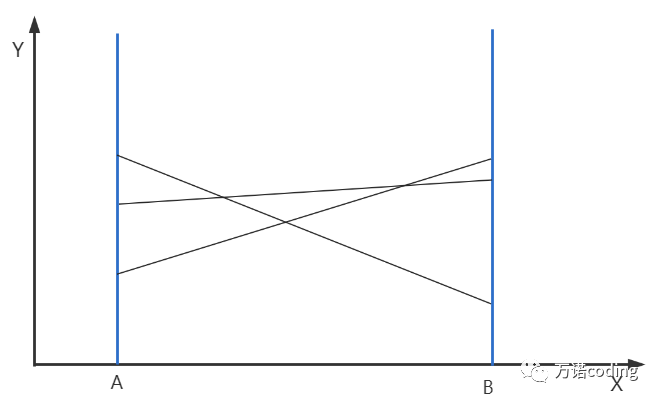
img

那么，如何快速計算某個時刻，在 X 坐標軸上[ A， B] 區間面積被直線劃分成多少塊？

A軸平行坐標Y軸，A (x=1)

B軸平行坐標Y軸, B(x = 20);

輸入描述

輸入采用多行輸入，一行4個數據，分別表示兩個坐標點，一行一條直線；

1，4，20,100 - 表兩個點，點t1的坐標為（1,4），點t2坐標為（20,100）

輸出描述

輸出為整數，表示被輸入線段劃分的面積個數

示例1

輸入

1,37,20,4
1,7,20,121

輸出

4

備注

AB之間的線段不平行于Y軸

思路

幾何題，當兩條線在這一區域內不相交時，區域空間增加1，當兩條線的交點在這一區域內時，空間增加2，所以我們判斷交點是否在區域內即可

代碼

 public static void main(String[] args) {Scanner in = new Scanner(System.in);List<int[]> edges = new ArrayList<>();int res = 1;while(in.hasNextLine()){String inputLine = in.nextLine();if (inputLine.isEmpty()) {break; // 如果輸入為空行，退出循環}res+=1;String[] line = inputLine.split(",");if(line[0]=="") continue;int[] nodes = new int[4];for(int i=0;i<4;i++){nodes[i] = Integer.parseInt(line[i]);}for(int[] edge:edges){double x = getIntersection(nodes[0],nodes[1],nodes[2],nodes[3],edge[0],edge[1],edge[2],edge[3]);if(x<20 && x>1) res+=1;}edges.add(nodes);}System.out.println(res);}static double getIntersection(int x1,int y1,int x2,int y2,int x3,int y3,int x4,int y4){double k1 = (y1-y2)/(x1-x2);double b1 = y1 - k1*x1;double k2 = (y4-y3)/(x4-x3);double b2 = y3 - k2*x3;double x = (b2-b1)/(k1-k2);return x;}

最佳面試策略

小明最近在找工作，收到了許多面試邀約，可參加的面試由interviews 數組表示，其中 interviews[i] = [startTimei, endTimei, possibilityi]，表示第 i 個面試在 startTimei 開始，endTimei 結束，面試成功的可能性是 possibilityi，該值越大，通過面試的可能性越大，由于精力限制，小明最多可以參加 k 場面試。

小明同一時間只能參加一場面試，如果要參加某場面試，必須完整參加這場面試才可能通過面試，即不能同時參加一個開始時間和另一個結束時間相同的兩場面試。

請給出小明面試成功可能性的最大和。

示例1

輸入

[[1,2,3],[3,4,2],[2,4,4]],2

輸出

5

說明

小明參加?[1,?2,?3]，?[3,?4,?2]?兩場面試，面試通過可能性的和為?3?+?2?=?5

示例2

輸入

[[1,2,3],[3,4,2],[2,4,6]],2

輸出

6

說明

只參加面試?[2,?4,?6]，面試通過的可能性的和最大，為?6?

思路

?對于這道題，我們先定義dp的狀態，dp[i][j]為面對i這個時間段的面試，已經面試了j次，決策后的最大可能值

先對interviews根據左端的值進行排序。

然后從后往前遍歷interviews，使用二分搜索的方法算出當前面試i的下一場面試，然后我們逐次消耗面試次數，記錄消耗j次面試機會的最大可能值，與進行下一次面試的值做比較，得到最終的最大值

注意，這里我們記錄了dp[i+1][j]的值，就是當這個可能值 > i加上后面的面試的可能值時，會保留更大的那個可能值的結果

代碼

import java.util.Arrays;public class algorithm {public static void main(String[] args) {int[][] s = { {1,2,3},{3,4,2},{2,4,6} };System.out.println(maxValue(s,2));}public static int maxValue(int[][] interviews,int k){Arrays.sort(interviews,(a,b)->a[0]-b[0]);int n = interviews.length;int[][] dp = new int[n+1][k+1];for(int i=n-1;i>=0;i--){int l=i,r=n;while (l<r){int mid = (l+r)>>1;if(interviews[i][1]<interviews[mid][0]) r=mid;else l=mid+1;}for(int j=0;j<=k;j++){dp[i][j] = dp[i+1][j];if(j>0) dp[i][j] = Math.max(dp[i][j],dp[r][j-1]+interviews[i][2]);}}return dp[0][k];}}

星球間的最短通路

在一個遙遠的銀河中，有N個星球（編號從1到N），這些星球之間通過星際門進行連接。每個星際門都連接兩個星球，并且可以雙向通行。

每個星際門的開啟需要消耗一定的能量，這個能量由星際門上的數字表示。每個星際門上的數字都是唯一的。

現在，由于某種原因，所有的星際門都處于關閉狀態。作為一個探索者，你的任務是找出一種方式，開啟最少的星際門，使得所有的星球都至少通過一個開啟的星際門與其他星球連接。

給你一些可連接的選項 connections，其中 connections[i] = [Xi, Yi, Mi] 表示星球 Xi 和星球 Yi 之間可以開啟一個星際門，并消耗 Mi 能量。

計算聯通所有星球所需的最小能量消耗。如果無法聯通所有星球，則輸出-1。

示例1

輸入

3,[[1,?2,?5],?[1,?3,?6],?[2,?3,?1]]

輸出

6

備注

1?≤?N?≤?100

思路

使用克魯斯卡爾算法求最小圖，這其中使用到了并查集的東西

代碼

import java.util.Arrays;public class Main {int[] fa;void init(int n){fa = new int[n];for(int i=0;i<n;i++) fa[i] = i;}int find(int x){return x == fa[x]? x: (fa[x] = find(fa[x] ));}void union(int x,int y){fa[find(x)] = find(y);}public int minimumCost(int n,int[][] connections){init(20000);Arrays.sort(connections,(a,b)->a[2]-b[2]);int ans = 0;for(int[] arr:connections){int a = arr[0],b=arr[1],w=arr[2];if(find(a)!=find(b)){union(a,b);ans+=w;}}return ans;}public static void main(String[] args) {Main a = new Main();int[][] s = {{1, 2, 5}, {1, 3, 6}, {2, 3, 1}};System.out.println(a.minimumCost(3,s));}
}