引入

配對堆是一個支持插入，查詢/刪除最小值，合并，修改元素等操作的數據結構，是一種可并堆。有速度快和結構簡單的優勢，但由于其為基于勢能分析的均攤復雜度，無法可持久化。

定義

配對堆是一棵滿足堆性質的帶權多叉樹（如下圖），即每個節點的權值都小于或等于他的所有兒子（以小根堆為例，下同）。

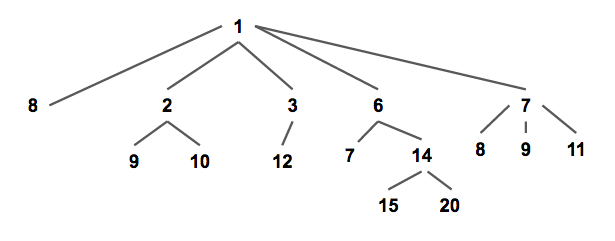
通常我們使用兒子 - 兄弟表示法儲存一個配對堆（如下圖），一個節點的所有兒子節點形成一個單向鏈表。每個節點儲存第一個兒子的指針，即鏈表的頭節點；和他的右兄弟的指針。

這種方式便于實現配對堆，也將方便復雜度分析。

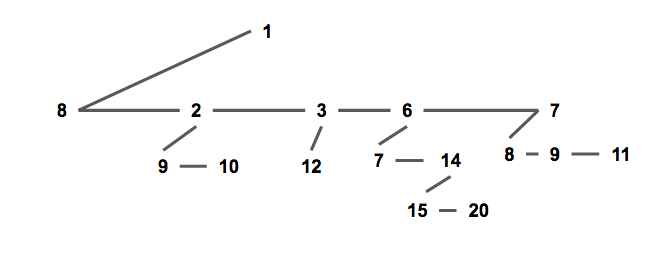
struct Node {T v;  // T為權值類型Node *child, *sibling;// child 指向該節點第一個兒子，sibling 指向該節點的下一個兄弟。// 若該節點沒有兒子/下個兄弟則指針指向 nullptr。
};

從定義可以發現，和其他常見的堆結構相比，配對堆不維護任何額外的樹大小，深度，排名等信息（二叉堆也不維護額外信息，但它是通過維持一個嚴格的完全二叉樹結構來保證操作的復雜度），且任何一個滿足堆性質的樹都是一個合法的配對堆，這樣簡單又高度靈活的數據結構奠定了配對堆在實踐中優秀效率的基礎；作為對比，斐波那契堆糟糕的常數就是因為它需要維護很多額外的信息。

配對堆通過一套精心設計的操作順序來保證它的總復雜度，原論文1將其稱為「一種自調整的堆（Self Adjusting Heap）」。在這方面和 Splay 樹（在原論文中被稱作「Self Adjusting Binary Tree」）頗有相似之處。

過程

查詢最小值

從配對堆的定義可看出，配對堆的根節點的權值一定最小，直接返回根節點即可。

合并

合并兩個配對堆的操作很簡單，首先令兩個根節點較小的一個為新的根節點，然后將較大的根節點作為它的兒子插入進去。（見下圖）

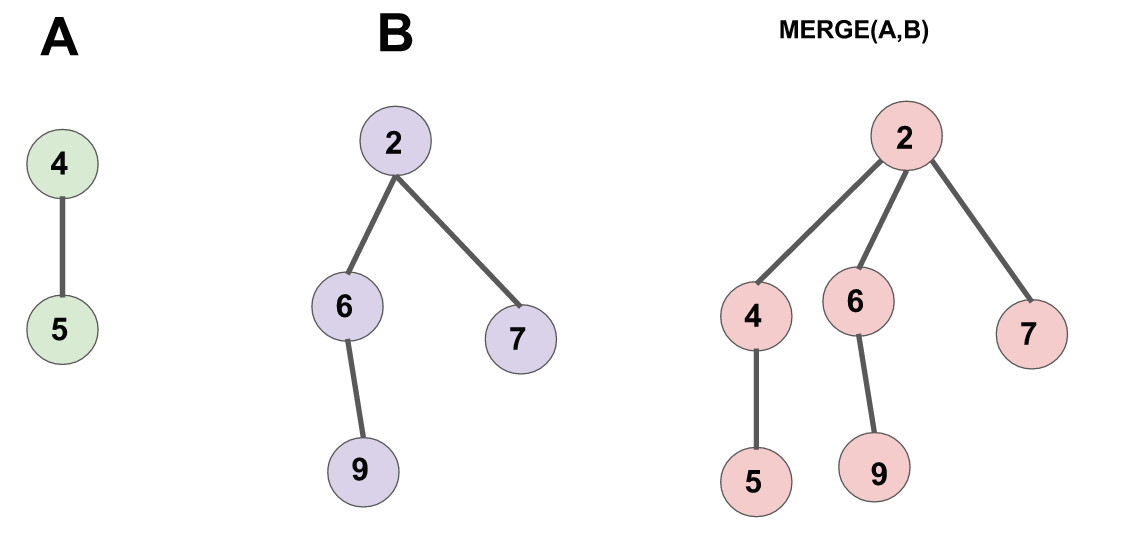
需要注意的是，一個節點的兒子鏈表是按插入時間排序的，即最右邊的節點最早成為父節點的兒子，最左邊的節點最近成為父節點的兒子。

實現

Node* meld(Node* x, Node* y) {// 若有一個為空則直接返回另一個if (x == nullptr) return y;if (y == nullptr) return x;if (x->v > y->v) std::swap(x, y);  // swap后x為權值小的堆，y為權值大的堆// 將y設為x的兒子y->sibling = x->child;x->child = y;return x;  // 新的根節點為 x
}

插入

合并都有了，插入就直接把新元素視為一個新的配對堆和原堆合并就行了。

刪除最小值

首先要提及的一點是，上文的幾個操作都十分偷懶，完全沒有對數據結構進行維護，所以我們需要小心設計刪除最小值的操作，來保證總復雜度不出問題。

根節點即為最小值，所以要刪除的是根節點。考慮拿掉根節點之后會發生什么：根節點原來的所有兒子構成了一片森林；而配對堆應當是一棵樹，所以我們需要通過某種順序把這些兒子全部合并起來。

一個很自然的想法是使用 $meld$ 函數把兒子們從左到右挨個并在一起，這樣做的話正確性是顯然的，但是會導致單次操作復雜度退化到 $O(n)$。

為了保證總的均攤復雜度，需要使用一個「兩步走」的合并方法：

1.把兒子們兩兩配成一對，用 meld 操作把被配成同一對的兩個兒子合并到一起（見下圖 1），
2.將新產生的堆** 從右往左**（即老的兒子到新的兒子的方向）挨個合并在一起（見下圖 2）。

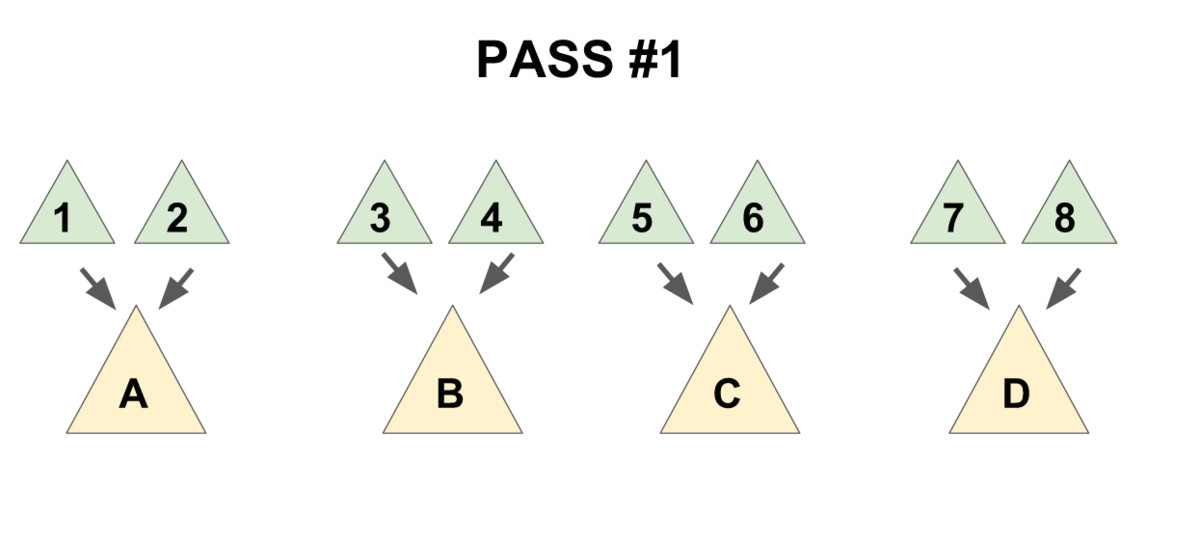
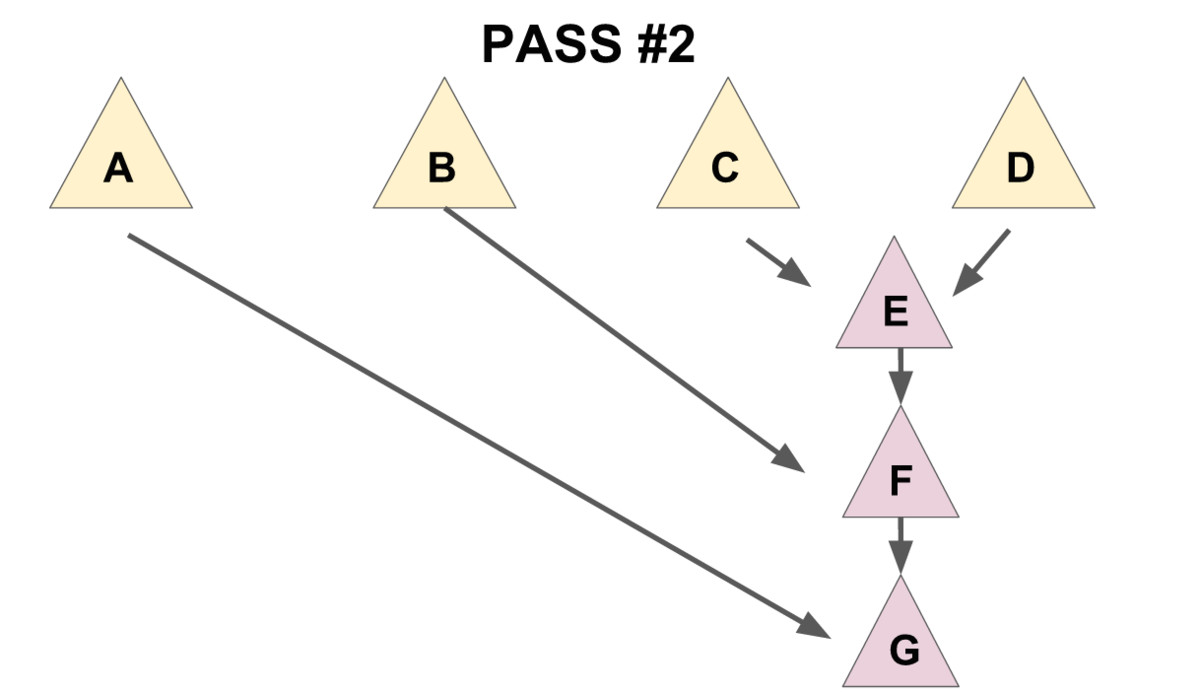
先實現一個輔助函數merges，作用是合并一個節點的所有兄弟。

實現

Node* merges(Node* x) {if (x == nullptr || x->sibling == nullptr)return x;  // 如果該樹為空或他沒有下一個兄弟，就不需要合并了，return。Node* y = x->sibling;                // y 為 x 的下一個兄弟Node* c = y->sibling;                // c 是再下一個兄弟x->sibling = y->sibling = nullptr;   // 拆散return meld(merges(c), meld(x, y));  // 核心部分
}

最后一句話是該函數的核心，這句話分三部分：
1.meld(x,y)「配對」了 x 和 y。
2.merges( c ) 遞歸合并 c 和他的兄弟們。
3.將上面 2 個操作產生的 2 個新樹合并。

需要注意到的是，上文提到了第二步時的合并方向是有要求的（從右往左合并），該遞歸函數的實現已保證了這個順序，如果讀者需要自行實現迭代版本的話請務必注意保證該順序，否則復雜度將失去保證。

有了 merges 函數，delete-min 操作就顯然了。

Node* delete_min(Node* x) {Node* t = merges(x->child);delete x;  // 如果需要內存回收return t;
}

減小一個元素的值

要實現這個操作，需要給節點添加一個「父」指針，當節點有左兄弟時，其指向左兄弟而非實際的父節點；否則，指向其父節點。

首先節點的定義修改為：

struct Node {LL v;int id;Node *child, *sibling;Node *father;  // 新增：父指針，若該節點為根節點則指向空節點 nullptr
};

meld 操作修改為：

Node* meld(Node* x, Node* y) {if (x == nullptr) return y;if (y == nullptr) return x;if (x->v > y->v) std::swap(x, y);if (x->child != nullptr) {  // 新增：維護父指針x->child->father = y;}y->sibling = x->child;y->father = x;  // 新增：維護父指針x->child = y;return x;
}

merges操作修改為：

Node *merges(Node *x) {if (x == nullptr) return nullptr;x->father = nullptr;  // 新增：維護父指針if (x->sibling == nullptr) return x;Node *y = x->sibling, *c = y->sibling;y->father = nullptr;  // 新增：維護父指針x->sibling = y->sibling = nullptr;return meld(merges(c), meld(x, y));
}

現在我們來考慮如何實現 decrease-key 操作。
首先我們發現，當我們減少節點 x 的權值之后，以 x 為根的子樹仍然滿足配對堆性質，但 x 的父親和 x 之間可能不再滿足堆性質。
因此我們把整棵以 x 為根的子樹剖出來，現在兩棵樹都符合配對堆性質了，然后把他們合并起來，就完成了全部操作。

// root為堆的根，x為要操作的節點，v為新的權值，調用時需保證 v <= x->v
// 返回值為新的根節點
Node *decrease_key(Node *root, Node *x, LL v) {x->v = v;                 // 更新權值if (x == root) return x;  // 如果 x 為根，則直接返回// 把x從fa的子節點中剖出去，這里要分x的位置討論一下。if (x->father->child == x) {x->father->child = x->sibling;} else {x->father->sibling = x->sibling;}if (x->sibling != nullptr) {x->sibling->father = x->father;}x->sibling = nullptr;x->father = nullptr;return meld(root, x);  // 重新合并 x 和根節點
}

復雜度分析

配對堆結構與實現簡單，但時間復雜度分析并不容易。

原論文1僅將復雜度分析到 meld 和 delete-min 操作均為均攤 $O(\log n)$，但提出猜想認為其各操作都有和斐波那契堆相同的復雜度。

遺憾的是，后續發現，不維護額外信息的配對堆，在特定的操作序列下，decrease-key 操作的均攤復雜度下界至少為 $\Omega (\log \log n)2$。

目前對復雜度上界比較好的估計有，Iacono 的 $O(1)$ meld，$O(\log n) $decrease；Pettie 的 $O(2^{2\sqrt{\log \log n}})$ meld 和 decrease。需要注意的是，前述復雜度均為均攤復雜度，因此不能對各結果分別取最小值。