死鎖的概念
- 死鎖:在并發環境下,個進程因為競爭資源而造成的一種互相等待對方手里的資源,導致各進程都阻塞,無法向前推進的現象。
 區別:
區別:
- 饑餓:由于長期得不到想要的資源進程無法向前推進的現象。
- 死循環:程序運行無法停止的狀態。

死鎖產生的必要條件
- 互斥條件:資源是互斥使用的,只能被有限進程同時使用。(像內存、揚聲器這樣的資源不會發生死鎖)
- 不剝奪條件:進程所獲得的資源在未使用完之前不能由其他進程奪走,只能主動釋放。
- 請求和保持條件:進程已經保持了至少一個資源,但是又提出請求新的資源,當無法獲取新資源的時候阻塞,保持已經占有的資源不放。
- 循環等待:存在一種進程資源的循環等待鏈,鏈中的每一個進程以獲得的資源同時被下一個進程請求。循環等待不一定會發生死鎖,但是死鎖一定會有循環等待現象發生。
需要注意的是上述條件都是必要條件。如果同類資源數大于1,則有循環等待也未必發生死鎖,但是如果每個資源只有一個的,那么循環等待就是死鎖的充分必要條件。
死鎖產生的時期
- 對不可剝奪系統資源的競爭
- 進程推進順序非法
- 信號量使用不當
死鎖的處理策略
- 預防死鎖:破壞死鎖產生的四個必要條件中的一個或者幾個
- 避免死鎖:用某種方法防止系統進入不安全感的狀態,從而避免死鎖(例如銀行家算法)
- 死鎖的檢測和解除:允許死鎖的發生,如果檢測發生后需要進行解除
預防死鎖
破壞互斥條件
將互斥使用的資源改造為允許共享使用的資源。
例如:SPOOLing技術。操作系統可以采用SPOOLing技術把獨占設備在邏輯上改造成共享設備。使用的方法就是增加了一個專門用于調度專用資源的進程。這樣對于其他進程來講自己的進程就立馬被處理了,而不會造成阻塞。
缺點:并不是所有的資源都可以改造成共享使用的資源,為了系統安全,許多地方必須保護這種互斥性,因此很多時候我們無法破壞這種互斥性。
破壞不剝奪條件
方案一:當某個進程請求新的資源得不到滿足時,他必須釋放所保持的所有資源,待以后需要的時候再主動申請。(即使自己還沒有使用結束)
方案二:當某個進程需要使用被占用的資源的時候,可以由操作系統協助將想要的資源強制剝奪。這種方式一般需要考慮各進程的優先級。
缺點:
- 實現起來比較復雜
- 釋放已經獲得的資源可能造成前一段工作的失效。因此這種方法一般只適用于已保存和恢復的資源,例如CPU。
- 反復的申請和釋放資源會增加系統開銷,降低系統吞吐量。
- 采用方案一的話如果得不到某個資源則之前的資源都需要放棄,以后再重新申請,這樣有可能導致進程的饑餓。
破壞請求和保持條件
- 靜態分配方法:在進程運行前一次申請完它所需要的全部進程,在他的資源未滿足前不讓他投入運行,一旦投入運行后這些資源就一直歸他所有。
實現簡單。缺點明顯:資源利用率極低,而且可能導致某些進程饑餓。
破壞循環等待條件
- 順序資源分配法:首先給系統中的資源編號,規定每個進程必須按照編號遞增的順序請求資源,同類資源(編號相同的資源)一次性申請完。
原理分析:只有擁有小編號資源的進程等待大編號資源,而不會有擁有大編號資源的進程等待小編號資源,從而防止了循環等待現象的發生。
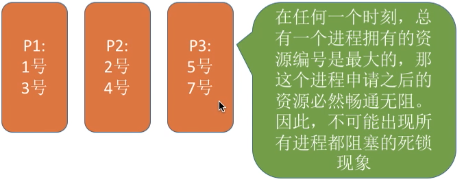
缺點:
- 不方便增加新的設備,因為可能需要重新分配編號
- 進程實際使用資源的順序可能和編號遞增的順序不一樣從而導致資源的浪費。如果想要解決這個問題,就必須按照規定次序申請資源,用戶編程麻煩。
避免死鎖
安全序列:如果系統按照安全序列分配資源,則每個進程都能夠順利完成。只要能和造出一個安全序列,系統就是安全狀態。當然安全狀態可能有多個。
如果分配了資源以后,系統找不出任何一個安全序列,則系統進入不安全狀態。這就意味著之后可能所有進程都無法順利執行下去。當然,如果有進程提前歸還了一些資源,則系統也有可能重新回到安全狀態。
如果系統處于安全狀態,就一定不會發生死鎖。如果系統進入不安全狀態,就可能發生死鎖(處于不安全狀態未必就是發生了死鎖。但是發生死鎖一定是在不安全狀態)
因此可以在資源分配之前與預先判斷分配是否會導致系統進入不安全狀態,以此決定是否答應資源分配請求。
銀行家算法
核心思想:在進程提出資源申請時,先預判此次分配是否會導致系統進入不安全狀態。如果會進入不安全狀態,就暫時不答應這次請求,讓該進程先被阻塞等待。
 數據結構:
數據結構:
- 長度為m的一維數組
Available表示還有多少可用資源 - n*m矩陣
Max表示各個進程對資源的最大需求數 - n*m矩陣
Allocation表示已經給個進程分配了多少資源 - n*m矩陣
Need表示各進程還需要多少資源 - 長度為m的一維數組
Request表示進程此次申請的各種資源數
銀行家算法步驟:
- 檢查此次申請是否超過了最大需求數
- 檢查此時系統剩余的可用資源是否還能滿足這次請求
- 試探著分配,更改各數據結構(
AvailableAllocationNeed) - 用安全性算法檢查此次分配是否會導致系統進入不安全狀態
安全性算法步驟:
- 檢查當前剩余可用資源能否滿足某個進程的最大需求,如果可以,就將該進程加入安全序列,并把該進程持有的資源全部回收
- 不斷重復上述過程,檢查最終能否將所有進程都加入安全序列
死鎖的檢測和解除
如果不采取預防思索的措施,也不采取避免死鎖的措施,系統很有可能發生死鎖。這個時候就應該進行死鎖的檢測和解除。
死鎖的檢測
資源分配圖:

如果系統中剩余的可用資源足夠滿足進程的需求,那么這個進程是不會阻塞的,可以順利執行下去。執行結束后消除與該進程相連的所有邊(歸還資源)。
如果按照上述過程最終能夠消除所有邊,則稱這個圖是可完全簡化的。此時一定沒有發生死鎖。(相當于找到一個安全序列)
如果不能消除所有邊,那么此時就是發生了死鎖。
檢測死鎖的算法:
- 在資源分配圖中,找出既不阻塞又不是孤點的進程,消去它所有的請求邊和分配邊,使之成為孤立的節點。
- 重復上面的過程,直至資源分配圖變成可完全簡化的。
死鎖定理:如果某時刻的資源分配圖是不可完全簡化的,那么此時可系統死鎖。
死鎖的解除
并不是系統中所有進程都是死鎖狀態,用死鎖檢測算法化簡資源分配圖以后,還連著邊的那些進程就是死鎖進程。
解除死鎖的主要方法有:
- 資源剝奪法。掛起(暫時放到外存上)某些死鎖進程,并搶占它的資源,將這些資源分配給其他死鎖進程。但是應該防止被掛起的進程長時間得不到資源而饑餓。
- 撤銷進程法(終止進程法)。強制撤銷部分、甚至全部死鎖的進程,并剝奪這些進程的資源。實現簡單,代價較大。
- 進程回退法:讓一個或者多個死鎖進程回退到可以避免死鎖的地步。這就要求系統記錄進程的歷史信息,設置還原點。
應該奪取哪個進程的資源:
- 進程優先級
- 已執行時間
- 還有多久能夠完成
- 進程已經使用了多少資源
- 進程是交互式的還是批處理式的(優先犧牲批處理)


)
)





)
)
)




)


