今天（準確說是昨天，一下子就過12點了）下午剛參加了CSP認證考試，大概是考了220（前兩題AC，第三題太折磨了懶得看了，后面兩題各混了10分），唯一有點參與感的就是B題了，于是這里分析下我的B題思路。

題意：對于$n?n$的矩陣，求存在多少個這樣的點（以該點為中心半徑為 $r$ 正方形塊中的總值的平均數不大于閾值 $t$ ）

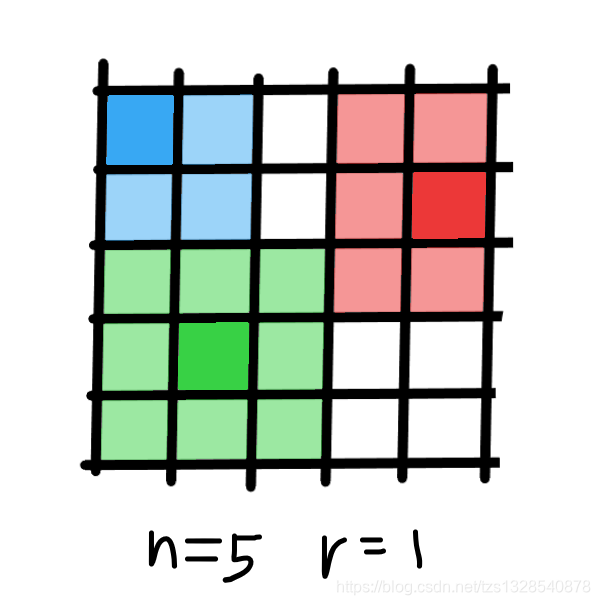
思路：如上圖所示，靠邊緣的點所形成的方塊是不完整的，當時第一遍我是打算用dp計算中央部分完整的塊，而對于邊緣不完整的塊則采用暴力，實現起來比較簡單，沒想到的是有30%($n<=600,r<=100$)TLE了，碼代碼前只是粗略的計算了一下時間復雜度，感覺能過。于是又想到了下面的方法，消除了暴力的部分。

人為地將矩陣向外擴充 $r$ 個單位，這樣就避免了靠近邊緣的點形成不完整的方塊，并且對于擴充的格子均填上閾值 $t$ ，這樣在計算平均值時又保持了原方塊的平均值與閾值的大小關系

$$\begin{gathered} \frac{sum}{m}\le t\to sum\le m?t \\ sum+(n?t)\le m?t+(n?t) \\ sum+(n?t)\le (m+n)?t \\ \frac{sum+n?t}{m+n}\le t \end{gathered}$$

dp的部分有空再分析分析，現在得睡覺了。。

代碼：（賽后重寫了一遍，沒交過，不保證AC）

#include<bits/stdc++.h>
#define debug1(x) cout<<#x<<":"<<x<<endl
typedef long long ll;
typedef unsigned long long ull;
const int N = 1000;
using namespace std;
int a[N][N], dp[N][N],row[N],col[N][N];
int n,L,r,t,R;
void init()
{for(int i = 0; i < N; i++){row[i] = -1;for(int j = 0; j < N; j++){a[i][j] = t;col[i][j] = -1;}}
}
int calc_row(int i)
{if(row[i] == -1){int sum = 0;for(int j = 0 - r; j <= 0 + r; j++) sum += a[i][R + j];row[i] = sum;}return row[i];
}
int calc_col(int i, int j)
{if(col[i - 1][j] == -1){int sum = 0;for(int k = i - r; k <= i + r; k++) sum += a[k][j];col[i][j] = sum;}else{col[i][j] = col[i - 1][j] + a[i + r][j] - a[i - 1 - r][j];}return col[i][j];
}
int main()
{cin>>n>>L>>r>>t;R = r + 5;init();for(int i = 0; i < n; i++){for(int j = 0; j < n; j++){scanf("%d",&a[R + i][R + j]);}}// calculate dp[0][0]for(int i = 0 - r; i <= 0 + r; i++){for(int j = 0 - r; j <= 0 + r; j++){dp[0][0] += a[R + i][R + j];}}for(int i = 0; i < n; i++){if(i){int sub_row = calc_row(R + i - 1 - r);int add_row = calc_row(R + i + r);dp[i][0] = dp[i - 1][0] + add_row - sub_row;}for(int j = 1; j < n; j++){int sub_col = calc_col(R + i, R + j - 1 - r);int add_col = calc_col(R + i, R + j + r);dp[i][j] = dp[i][j - 1] + add_col - sub_col;}}int ans = 0, block = (2 * r + 1)*(2 * r + 1);for(int i = 0; i < n; i++){for(int j = 0; j < n; j++){if(dp[i][j] <= t * block) ans++;}}cout<<ans<<"\n";return 0;
}

剛去學習了一下二維前綴和的知識，果然比自己寫的dp簡約多了！

代碼：采用二維前綴和+人為擴矩（依舊不保證正確，目前還沒機會交）

#include<bits/stdc++.h>
#define debug1(x) cout<<#x<<":"<<x<<endl
typedef long long ll;
typedef unsigned long long ull;
const int N = 1000;
using namespace std;
int a[N][N], dp[N][N], s[N][N];
int n,L,r,t,R;
void init()
{for(int i = 0; i < N; i++){for(int j = 0; j < N; j++){a[i][j] = t;}}
}int main()
{cin>>n>>L>>r>>t;R = r + 5;init();for(int i = 0; i < n; i++){for(int j = 0; j < n; j++){scanf("%d",&a[R + i][R + j]);}}for(int i = 0 - r; i < n + r; i++){for(int j = 0 - r; j < n + r; j++){s[R + i][R + j] = s[R + i - 1][R + j]+ s[R + i][R + j - 1]- s[R + i - 1][R + j - 1]+ a[R + i][R + j];}}int i1,j1,i2,j2,sum;int ans = 0, block = (2 * r + 1)*(2 * r + 1);for(int i = 0; i < n; i++){for(int j = 0; j < n; j++){i1 = R + i - r; i2 = R + i + r;j1 = R + j - r; j2 = R + j + r;sum = s[i2][j2]- s[i2][j1 - 1]- s[i1 - 1][j2]+ s[i1 - 1][j1 - 1];if(sum <= t * block) ans++;}}cout<<ans<<"\n";return 0;
}

A題：比較基礎的統計題，按題目要求統計每個數出現的次數即可

#include<bits/stdc++.h>
#define debug1(x) cout<<#x<<":"<<x<<endl
typedef long long ll;
typedef unsigned long long ull;
using namespace std;
int main()
{int n, m, L;cin>>n>>m>>L;vector<int> ans(L);int tmp;for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){scanf("%d",&tmp);ans[tmp]++;}}for(int i = 0; i < L; i++) cout<<ans[i]<<" ";return 0;
}