1 KMP算法

原文鏈接：https://zhuanlan.zhihu.com/p/83334559

先約定，本文用pat表示模式串，長度為M，txt表示文本串，長度為N，KMP算法是在txt中查找子串pat，如果找到，返回這個子串的起始索引，否則返回-1.

用一張圖演示一下KMP算法：

KMP算法永不回退txt中的索引i，不走回頭路。而是借助一個數組dp，dp數組中存儲的信息把pat移到正確的位置繼續匹配。

KMP的難點在于計算dp數組，計算這個dp數組，之和pat有關。意思是說，只要給我個pat，我就能通過這個模式串計算出dp數組，與txt無關系。

dp 數組只和 pat 有關，那么我們這樣設計 KMP 算法就會比較漂亮：

int KMP(char *pat,char *txt)
{/*第一步獲取dp數組*/dp = getDP(char *pat);/* 第二步搜索*/return_value = search(char *txt,char *pat);/* 第三步 */return return_value;
}

狀態機概述

為什么說KMP算法與狀態機有關呢？是這樣的，我們可以認為pat的匹配就是狀態的轉移，比如pat=“ABABC”:

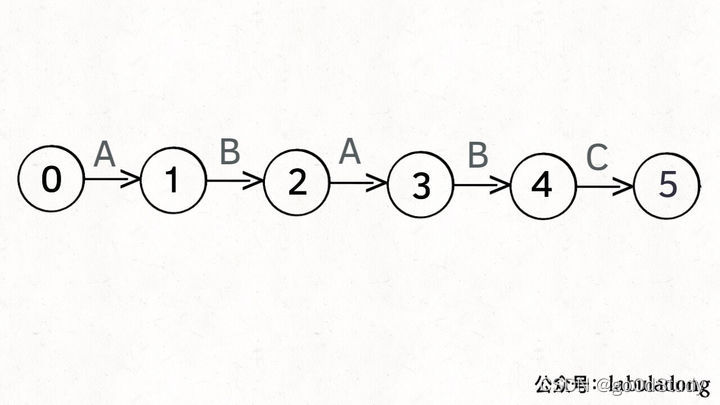
如上圖，圓圈內的數字就是狀態，狀態0是起始狀態，狀態5是終止狀態。開始匹配時pat處于起始狀態，一旦轉移到終止狀態，就說明在txt中找到了pat。比如說當前處于狀態2，說明字符AB被匹配。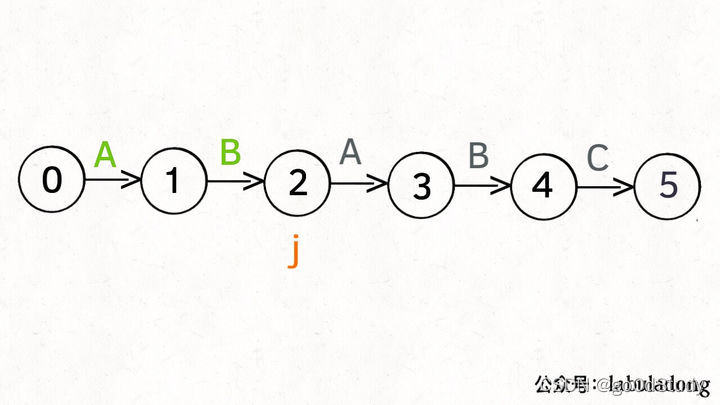
另外，當處于一個狀態時，接下來匹配的字符不同，pat 狀態轉移的行為也不同。比如說假設現在匹配到了狀態 4，如果遇到字符 A 就應該轉移到狀態 3，遇到字符 C 就應該轉移到狀態 5，如果遇到字符 B 就應該轉移到狀態 0：

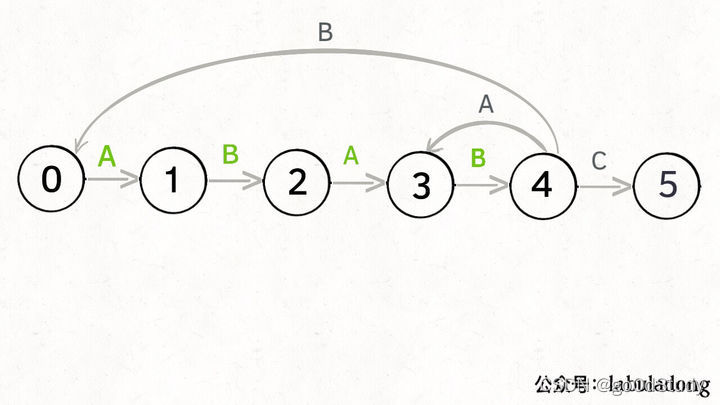
KMP算法最關鍵的步驟就是構造這個狀態轉移，要確定狀態轉移的行為，得確定兩個變量，一個是當前的匹配狀態，另一個是遇到的字符。確定了這兩個變量后，就可以知道這個情況下應該轉移到那個狀態。

為了描述狀態轉移圖，我們定義一個二維 dp 數組，它的含義如下：

dp[j][c] = next
0 <= j < M，代表當前的狀態
0 <= c < 256，代表遇到的字符（ASCII 碼）
0 <= next <= M，代表下一個狀態dp[4]['A'] = 3 表示：
當前是狀態 4，如果遇到字符 A，
pat 應該轉移到狀態 3
因為狀態3之前的字符和狀態4之前的字符相同dp[1]['B'] = 2 表示：
當前是狀態 1，如果遇到字符 B，
pat 應該轉移到狀態 2

根據我們這個dp數組和剛才狀態轉移的過程，我們可以先寫出KMP算法的search函數：

int search(char *txt,char *pat)
{int M = strlen(pat);int N = strlen(txt);//pat的初始態為0int  j = 0;for(int i=0;i<N;i++){/* 當前狀態是j，遇到字符txt[i]，pat應該轉移到那個狀態？ */j = dp[j][txt[i]];/* 如果到達終止態，返回匹配開頭的索引 */if(j==M) return i-M+1;}/* 沒有到達終止態，返回-1表示匹配失敗 */return -1;
}

構建狀態轉移

回想剛才說的：要確定狀態轉移的行為，必須明確兩個變量，一個是當前的匹配狀態，另一個是遇到的字符，而且我們已經根據這個邏輯確定了 dp 數組的含義，那么構造 dp 數組的框架就是這樣：

for 0 <= j < M: # 狀態for 0 <= c < 256: # 字符dp[j][c] = next

這個next狀態應該怎么求呢？顯然，如果遇到的字符c和pat[j]匹配，狀態就應該向前推進一個，也就是說next=j+1，我們不妨稱這種情況為狀態推進：

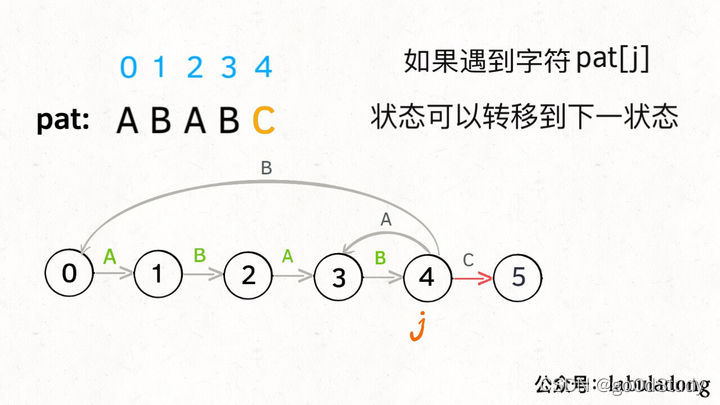
如果字符c和pat[j]不匹配，狀態就要回退（或者原地不動），我們不妨稱這種情況為狀態重啟：

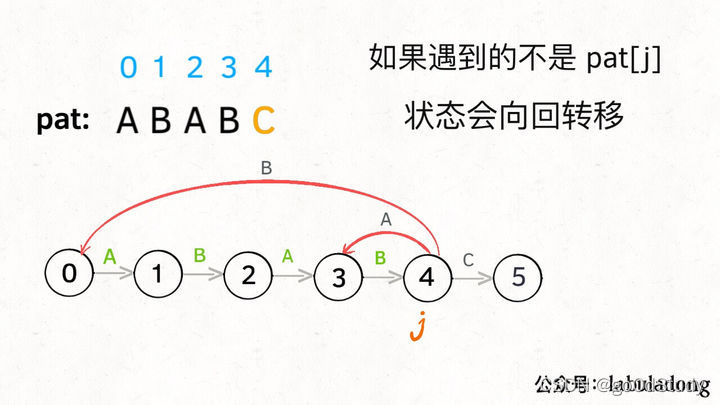
那么，如何得知在哪個狀態重啟呢？解答這個問題之前，我們再定義一個名字：影子狀態（我編的名字），用變量 X 表示。所謂影子狀態，就是和當前狀態具有相同的前綴。比如下面這種情況：

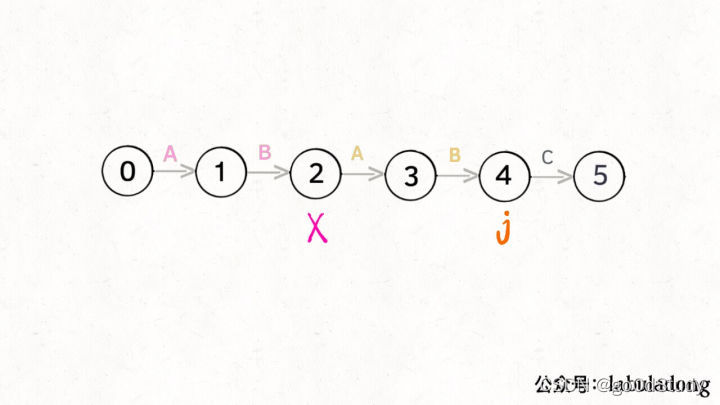
當前狀態j=4，其影子狀態為X=2，它們都有相同的前綴AB，因為狀態X和狀態j存在相同的前綴，所以當狀態j準備進行狀態重啟（遇到的字符c和pat[j]不匹配）的時候，可以通過X的狀態轉移來獲得最近的重啟位置。
比如說剛才的情況，如果狀態 j 遇到一個字符 “A”，應該轉移到哪里呢？首先只有遇到 “C” 才能推進狀態，遇到 “A” 顯然只能進行狀態重啟。狀態 j 會把這個字符委托給狀態 X 處理，也就是 dp[j]['A'] = dp[X]['A']

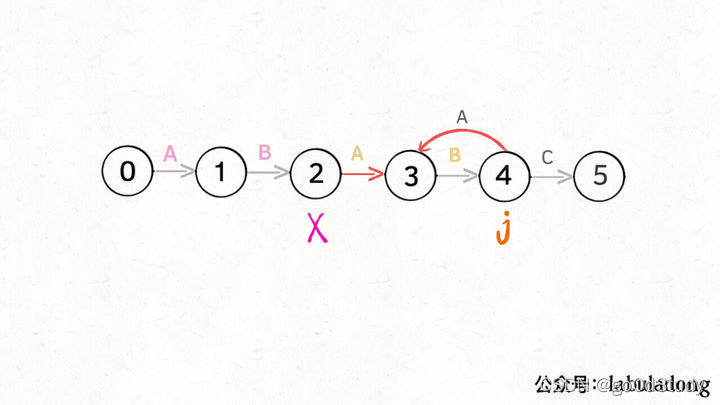
為什么這樣可以呢？因為：既然 j 這邊已經確定字符 “A” 無法推進狀態，只能回退，而且 KMP 就是要盡可能少的回退，以免多余的計算。那么 j 就可以去問問和自己具有相同前綴的 X，如果 X 遇見 “A” 可以進行「狀態推進」，那就轉移過去，因為這樣回退最少。

所以計算bp數組的偽代碼就有了：

int X # 影子狀態
for 0 <= j < M:for 0 <= c < 256:if c == pat[j]:# 狀態推進dp[j][c] = j + 1else: # 狀態重啟# 委托 X 計算重啟位置dp[j][c] = dp[X][c] # 更新 XX = dp[X][c]

為什么更新X使用的是： X = dp[X][c]，我們首先要理解dp的含義。看下圖：

dp[4]['A'] = 3 表示：
當前是狀態 4，如果遇到字符 A，
pat 應該轉移到狀態 3
因為狀態3之前的字符和狀態4之前的字符相同

狀態3前面的字符是ABA，狀態四前面有ABA（最后一個A是要匹配的），所以dp[4]['A'] = 3，dp[狀態n][匹配的字符y]的值實際代表的含義是在轉態n下pat字符串前面和后面能匹配的字符數（也就是前面說的影子）。

X = dp[X][c]表示在原來狀態下匹配字符c，如果相同的話，影子狀態就是增加1，如上圖，假設現在在狀態3匹配，則X=1，接下來就會計算dp[4]狀態下的轉移，在計算狀態4轉移前，首先要計算出狀態4對應的影子狀態，dp[X][c]就是比較X=1對應的字符B和狀態3對應的字符B是否相同，如果相同就是要增加影子長度，不相同就要轉移，計算對應的影子。

所以，getDP函數實現如下：

void getDP(char *pat,int M)
{/* dp[狀態][字符] = 下個狀態 */dp[0][pat[0]]= 1;int X=0;for(int j=1;j<M;j++){for(int c=0;c<256;c++){/* 和字符c匹配了 */if(pat[j]==c)dp[j][c]=j+1;else   /* 和字符c不匹配 */dp[j][c]=dp[X][c];}/* 更新 X*/X = dp[X][pat[j]];}
}

我們整合并化簡兩個程序，形成一個KMP算法。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>int dp[256][256];void getDP(char *pat,int M)
{/* dp[狀態][字符] = 下個狀態 */dp[0][pat[0]]= 1;int X=0;for(int j=1;j<M;j++){for(int c=0;c<256;c++){/* 和字符c匹配了 */if(pat[j]==c)dp[j][c]=j+1;else   /* 和字符c不匹配 */dp[j][c]=dp[X][c];}/* 更新 X*/X = dp[X][pat[j]];}
}int search(char *txt,char *pat)
{int M = strlen(pat);int N = strlen(txt);//pat的初始態為0int  j = 0;for(int i=0;i<N;i++){/* 當前狀態是j，遇到字符txt[i]，pat應該轉移到那個狀態？ */j = dp[j][txt[i]];/* 如果到達終止態，返回匹配開頭的索引 */if(j==M) return i-M+1;}/* 沒有到達終止態，返回-1表示匹配失敗 */return -1;
}int main(void)
{char *txt = "BCDABABC";char *pat = "ABABC";getDP(pat,strlen(pat));int count = search(txt,pat);printf("count = %d\n",count);return 0;
}