所有代碼塊都是在Jupyter Notebook下進行調試運行，前后之間都相互關聯。
文中所有代碼塊所涉及到的函數里面的詳細參數均可通過scikit-learn官網API文檔進行查閱，這里我只寫下每行代碼所實現的功能，參數的調整讀者可以多進行試驗調試。多動手！！！

主要內容：
線性回歸方程實現
梯度下降效果
對比不同梯度下降策略
建模曲線分析
過擬合與欠擬合
正則化的作用
提前停止策略

一、線性回歸

Ⅰ、參數直接求解法

前幾章節中也都得出求解的方案，基于最小二乘法直接求解，但這是人工進行求解，為此引入了梯度下降法來訓練機器學習。
回歸方程，也就是最小二乘法求解，確實回歸方程就是迭代更新即可。機器學習中核心的思想是迭代更新。
通過這些公式，我們需要把這個θ求解出來。

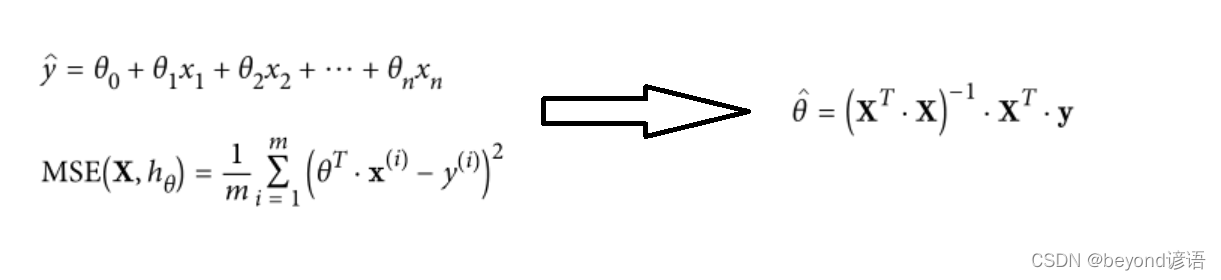
接下來，我們玩一個有意思的：將隨機生成100個點，然后再進行線性擬合，擬合出一條較好的直線。
以下代碼塊都是基于Jupyter notebook
導包

import numpy as np
import os
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)

# 隨機生成100個點，隨機構造一個方程y = 4 + 3*x + b
import numpy as np
X = 2*np.random.rand(100,1)#隨機構造數據，選取100個點構建矩陣
y = 4+ 3*X +np.random.randn(100,1)#隨機構造一個方程

# 顯示一下這些點
plt.plot(X,y,'g.')#顏色設定和隨機選取點
plt.xlabel('X_1')
plt.ylabel('y')
plt.axis([0,2,0,15])#x軸0-2和y軸0-15的取值范圍
plt.show()

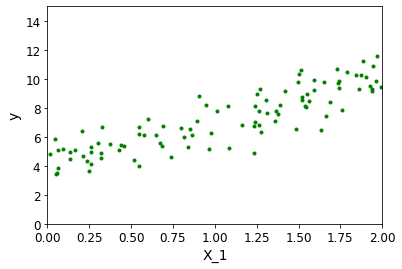
X_b = np.c_[np.ones((100,1)),X]#為了矩陣運算方便，需要再加一列全為1的向量，此時的X_b就是帶有偏置項的矩陣
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)#通過公式求解θ，.T轉置，.dot相乘，inv求逆

theta_best#得到偏置項和權重項
"""
array([[4.21509616],[2.77011339]])
"""

X_new = np.array([[0],[2]])#定義測試數據，兩個點就行，因為兩點就能確定一條直線
X_new_b = np.c_[np.ones((2,1)),X_new]#訓練的時候都加了一列1，測試的時候需要加一列1
y_predict = X_new_b.dot(theta_best)#當前得到的測試數據去乘以權重參數，得到最終的結果，相對于x×θ得到最后的y
y_predict#得出預測的結果值
"""
array([[4.21509616],[9.75532293]])
"""

X_new#當前的值
"""
array([[0],[2]])
"""

#將得到的結果進行繪制
plt.plot(X_new,y_predict,'b--')#由點x通過預測得到的y進行繪制
plt.plot(X,y,'g.')#上面的我們繪制的隨機點
plt.axis([0,2,0,15])
plt.show()

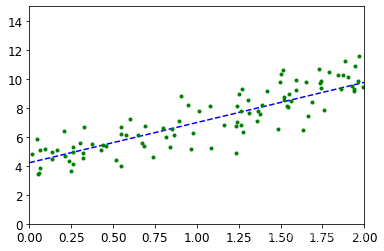
最終即可得到通過訓練一百個隨機數，進行擬合得權重參數θ，從而繪制出線性擬合直線。

工具包實現求解權重和偏置參數
sklearn api文檔

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
print (lin_reg.coef_)#權重參數
print (lin_reg.intercept_)#偏置參數
#很顯然，跟上述的求解的theta_best一致
"""
[[2.77011339]]
[4.21509616]
"""

Ⅱ、預處理對結果的影響

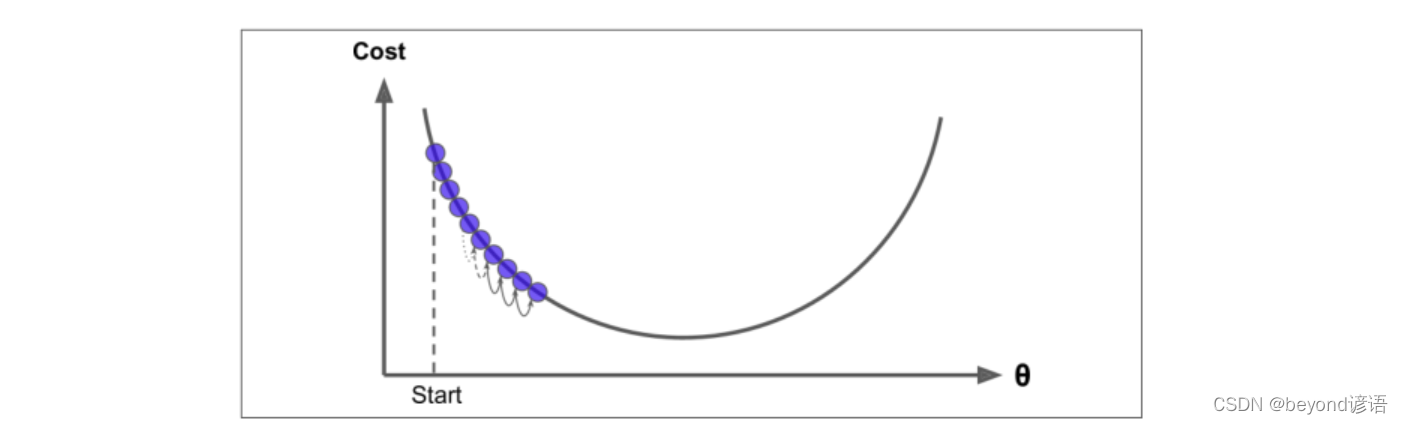
選擇一個初始值，沿著一個方向梯度按設置的步長走。

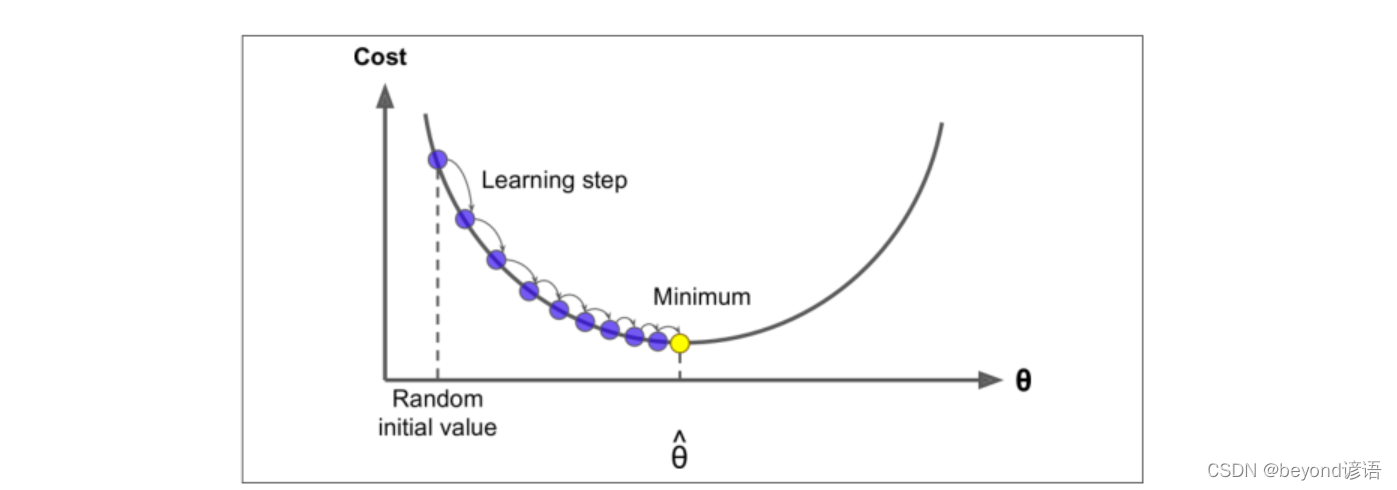
主要問題包括：
①步長的選取，過大容易發散，過小速度太慢

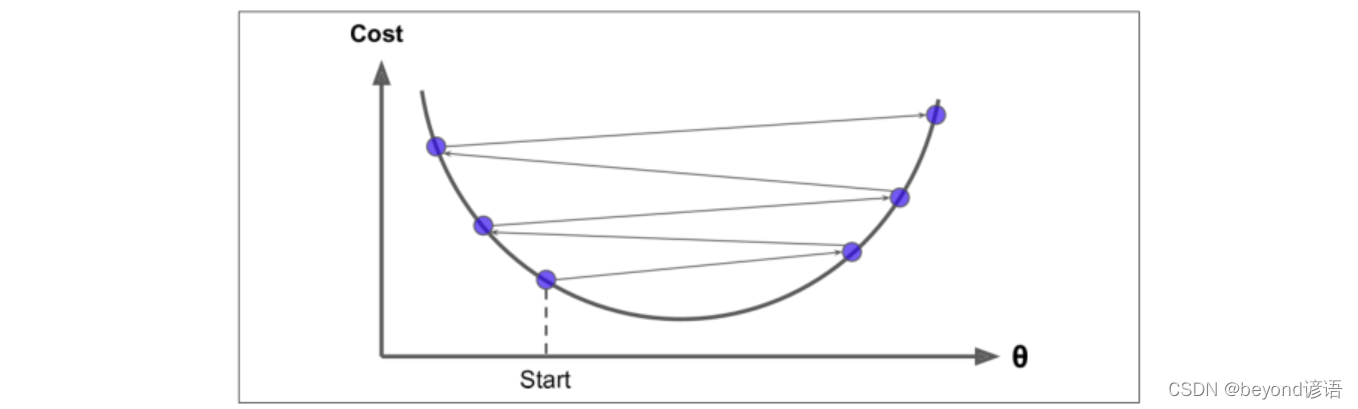
②局部最優解和全局最優解選取的問題

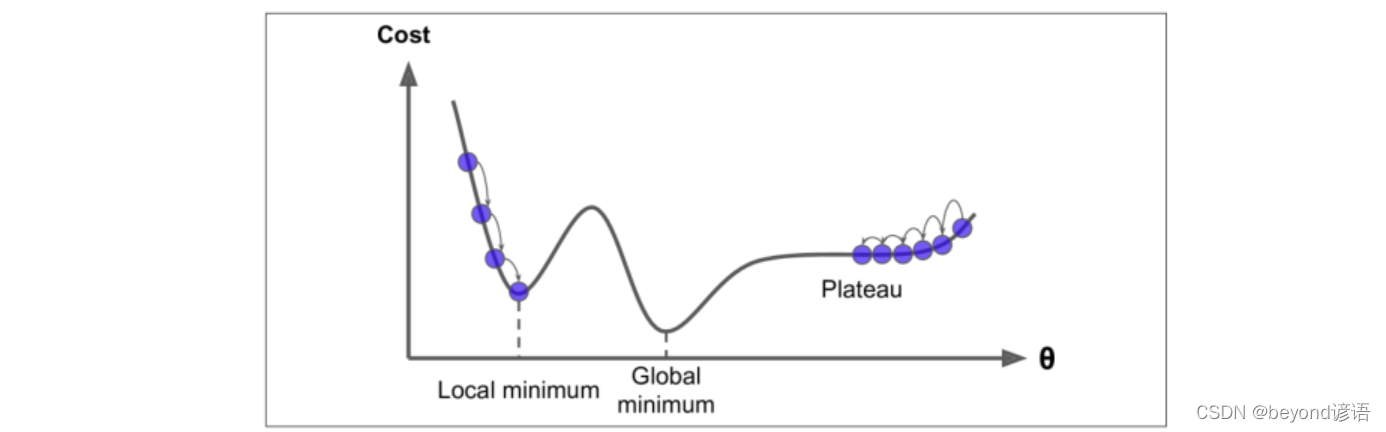
Ⅲ、標準化

標準化的作用：因為不同的特征取值范圍不同，比如年齡和工資，取值范圍肯定不同，故需要先對數據進行預處理，進行標準化歸一化操作。拿到數據之后基本上都需要做一次標準化操作

(x-μ)/σ，其中μ為均值，x-μ將所有的數據向坐標原點靠攏，以原點為中心對稱。σ為標準差，即數據的浮動范圍，取值范圍浮動大對應的標準差也大，除以σ使得數據取值范圍差不多一致。
綜合而言(x-μ)/σ就是將所有的數據向原點靠攏，以原點為中心對稱，每個數據的取值范圍差不多。

Ⅳ、梯度下降

①，批量梯度下降

批量梯度下降公式：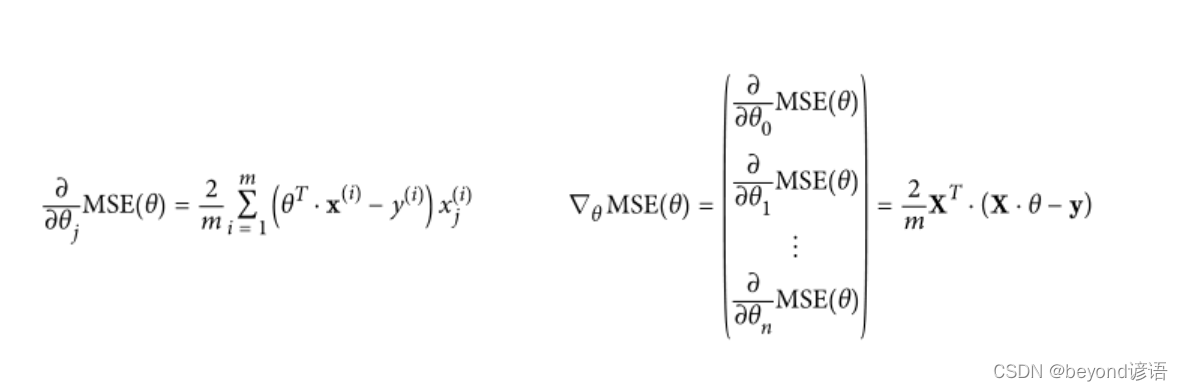

eta = 0.1#學習率
n_iterations = 1000#迭代次數
m = 100#樣本個數
theta = np.random.randn(2,1)#對權重參數隨機初始化
for iteration in range(n_iterations):#進行迭代gradients = 2/m* X_b.T.dot(X_b.dot(theta)-y)#每次迭代需要根據公式進行計算一下當前的梯度，這里是批量梯度下降使用了所用的樣本數據theta = theta - eta*gradients#更新參數

theta
"""
array([[4.21509616],[2.77011339]])
"""

X_new_b.dot(theta)#得出預測的結果值
#很顯然，跟上述的求解的theta_best一致
"""
array([[4.21509616],[9.75532293]])
"""

做個實驗：不同學習率α對結果的影響

theta_path_bgd = []#保存theta值用于后續的對比試驗
def plot_gradient_descent(theta,eta,theta_path = None):#theta_path指定是否要保存當前的實驗m = len(X_b)#一共的樣本個數plt.plot(X,y,'b.')#原始樣本數據進行散點圖顯示n_iterations = 1000#迭代次數for iteration in range(n_iterations):#遍歷每次迭代y_predict = X_new_b.dot(theta)#得到當前的預測值plt.plot(X_new,y_predict,'b-')#將預測的線性擬合結果進行繪制gradients = 2/m* X_b.T.dot(X_b.dot(theta)-y)theta = theta - eta*gradientsif theta_path is not None:#不是空值就進行保存theta_path.append(theta)plt.xlabel('X_1')plt.axis([0,2,0,15])#取值范圍plt.title('eta = {}'.format(eta))#把學習率當成圖的名稱

theta = np.random.randn(2,1)#隨機初始化一個θ值，因為需要偏置參數和權重參數故這里是兩個plt.figure(figsize=(10,4))#指定當前圖的大小
plt.subplot(131)#1列3個，首先畫第1個子圖
plot_gradient_descent(theta,eta = 0.02)
plt.subplot(132)#1列3個，畫第2個子圖
plot_gradient_descent(theta,eta = 0.1,theta_path=theta_path_bgd)
plt.subplot(133)#1列3個，畫第3個子圖
plot_gradient_descent(theta,eta = 0.5)
plt.show()#每根線都代表每次迭代得出的結果

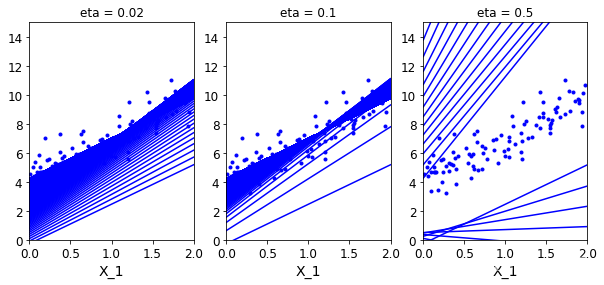
每條線都代表這每次迭代的結果，很明顯可以看出，學習率越小越慢，但效果好；學習率越大反而效果不好，學跑偏了都。

②，隨機梯度下降

theta_path_sgd=[]#保存theta值用于后續的對比試驗
m = len(X_b)#計算當前所有的樣本
np.random.seed(42)
n_epochs = 50#指定迭代次數t0 = 5#分子 隨便定義
t1 = 50#分母 隨便定義def learning_schedule(t):#學習率進行動態衰減，傳入迭代次數treturn t0/(t1+t)#t0和t1不變，t是迭代次數，隨著迭代次數的增加，整體會變小theta = np.random.randn(2,1)#對theta進行隨機初始化for epoch in range(n_epochs):#每個epoch表示完整的迭代一次所有的樣本for i in range(m):#一個epoch中完成了所有的樣本迭代if epoch < 10 and i<10:y_predict = X_new_b.dot(theta)#拿到預測結果值plt.plot(X_new,y_predict,'r-')#將預測結果值進行展示random_index = np.random.randint(m)#選取隨機的一個樣本xi = X_b[random_index:random_index+1]#取當前樣本的數據yi = y[random_index:random_index+1]#取當前樣本的標簽gradients = 2* xi.T.dot(xi.dot(theta)-yi)#通過隨機梯度下降公式計算梯度eta = learning_schedule(epoch*m+i)#沒每計算完一個梯度需要對學習率進行一次衰減theta = theta-eta*gradients#梯度更新theta_path_sgd.append(theta)#保存當前的theta值plt.plot(X,y,'b.')#繪制原始數據，以藍點的形式展示
plt.axis([0,2,0,15])#橫縱坐標的取值范圍
plt.show()#每次運行都會得到不同的結果

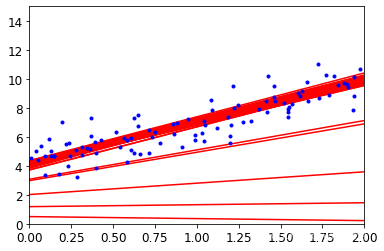
③，MiniBatch(小批量)梯度下降

theta_path_mgd=[]#保存theta值用于后續的對比試驗
n_epochs = 50#指定迭代次數
minibatch = 16
theta = np.random.randn(2,1)#對theta進行隨機初始化
#np.random.seed(0)#當然也可以指定隨機種子，保證每次隨機選取，最后的theta值的不變
t0, t1 = 200, 1000#指定衰減策略
def learning_schedule(t):return t0 / (t + t1)
np.random.seed(42)
t = 0
for epoch in range(n_epochs):shuffled_indices = np.random.permutation(m)#將常規的索引打亂順序X_b_shuffled = X_b[shuffled_indices]#將打亂之后的索引回傳到數據中y_shuffled = y[shuffled_indices]#標簽也一樣，需要傳入打亂之后的索引for i in range(0,m,minibatch):#從第0個樣本到第m個樣本，每個的大小為minibatcht+=1#記錄一下迭代次數xi = X_b_shuffled[i:i+minibatch]#從當前指定的位置開始，操作minibatch個yi = y_shuffled[i:i+minibatch]#標簽也一樣gradients = 2/minibatch* xi.T.dot(xi.dot(theta)-yi)#根據minibatch梯度計算公式計算梯度eta = learning_schedule(t)theta = theta-eta*gradientstheta_path_mgd.append(theta)

theta
"""
array([[4.25490684],[2.80388785]])
"""

Ⅴ、三種梯度下降策略對比

#為了方便后續的操作，將保存過的梯度都轉換為array格式
theta_path_bgd = np.array(theta_path_bgd)#批量梯度下降
theta_path_sgd = np.array(theta_path_sgd)#隨機梯度下降
theta_path_mgd = np.array(theta_path_mgd)#MiniBatch梯度下降

plt.figure(figsize=(12,6))#指定畫圖的最終大小
plt.plot(theta_path_sgd[:,0],theta_path_sgd[:,1],'r-s',linewidth=1,label='SGD')#隨機梯度下降，對兩個參數分別展示
plt.plot(theta_path_mgd[:,0],theta_path_mgd[:,1],'g-+',linewidth=2,label='MINIGD')#MiniBatch梯度下降
plt.plot(theta_path_bgd[:,0],theta_path_bgd[:,1],'b-o',linewidth=3,label='BGD')#批量梯度下降
plt.legend(loc='upper left')#label位置進行設置放在左上角
plt.axis([3.5,4.5,2.0,4.0])
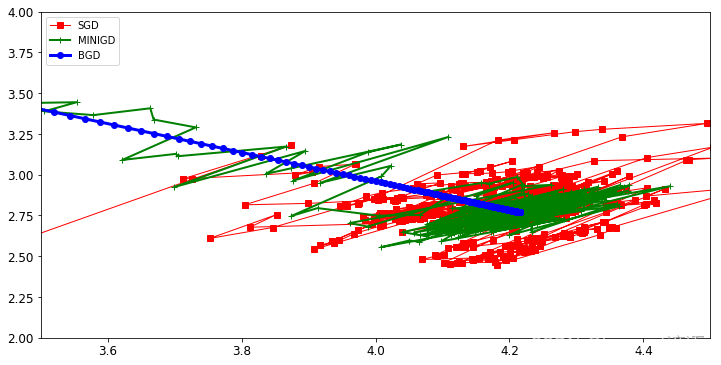
plt.show()
"""
藍色為批量梯度下降，直接奔著結果去的，不過很慢
綠色為MiniBatch梯度下降，隨機選取其中的幾個樣本為參數，因為每個樣本都不同，故有點跌宕起伏的感覺（常用，參數常用64、128、256，在速度能容忍的前提下參數越大越好）
紅色為隨機梯度下降，速度很快，跟個小傻子似的，好壞程度完全取決于隨機樣本選取的好壞
"""

二、多項式回歸

import numpy as np
import os
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)

m = 100#樣本數據個數
X = 6*np.random.rand(m,1) - 3#橫坐標的取值范圍[-3,3]
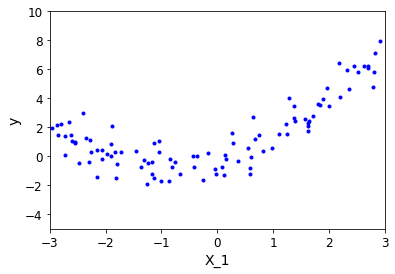
y = 0.5*X**2+X+np.random.randn(m,1)#自己隨便定義一個函數方程 y=0.5* x2 + x + b，其中b為高斯隨機抖動

plt.plot(X,y,'b.')#繪制隨機選取的離散點
plt.xlabel('X_1')#橫坐標名稱
plt.ylabel('y')#縱坐標名稱
plt.axis([-3,3,-5,10])#x、y的取值范圍
plt.show()

from sklearn.preprocessing import PolynomialFeatures#導入工具包
poly_features = PolynomialFeatures(degree = 2,include_bias = False)#對函數進行實例化操作
X_poly = poly_features.fit_transform(X)#fit執行所有的計算操作，transform將所有的計算結果進行整合回傳
X[0]#當前的x值
"""
array([2.82919615])
"""

X_poly[0]#[x,x2]
"""
array([2.82919615, 8.00435083])
"""

2.82919615 ** 2#很顯然就是x2值
"""
8.004350855174822
"""

from sklearn.linear_model import LinearRegression#導包。開始訓練
lin_reg = LinearRegression()
lin_reg.fit(X_poly,y)
print (lin_reg.coef_)#權重參數，即回歸方程y=1.1087967x + 0.53435278x2 - 0.03765461
print (lin_reg.intercept_)#與剛開始自定義的方程相比可知擬合效果還是很不錯的
"""
[[1.10879671 0.53435287]]
[-0.03765461]
"""

X_new = np.linspace(-3,3,100).reshape(100,1)#從[-3,3]中選擇100個測試數據
X_new_poly = poly_features.transform(X_new)#按照相同的規則對數據進行轉換
y_new = lin_reg.predict(X_new_poly)#使用剛才得到的回歸方程，得出預測值
plt.plot(X,y,'b.')#先畫隨機測試點
plt.plot(X_new,y_new,'r--',label='prediction')#再通過得出的預測值畫曲線
plt.axis([-3,3,-5,10])#顯示的時候限制一下取值范圍
plt.legend()#加上標簽
plt.show()

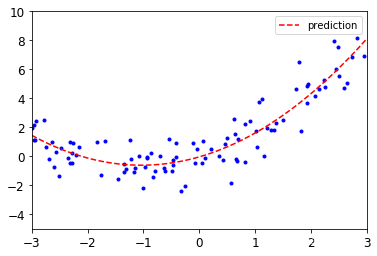
Ⅰ、根據不同degree值(不同多項式)進行擬合

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler#標準化操作
plt.figure(figsize=(12,6))
for style,width,degree in (('g-',1,100),('b--',1,2),('r-+',1,1)):#顏色、寬度、degree值poly_features = PolynomialFeatures(degree = degree,include_bias = False)#對函數進行實例化操作std = StandardScaler()#標準化 實例化lin_reg = LinearRegression()#線性回歸 實例化polynomial_reg = Pipeline([('poly_features',poly_features),('StandardScaler',std),('lin_reg',lin_reg)])#車間三部曲polynomial_reg.fit(X,y)#傳入數據y_new_2 = polynomial_reg.predict(X_new)#對測試點預測plt.plot(X_new,y_new_2,style,label = 'degree   '+str(degree),linewidth = width)
plt.plot(X,y,'b.')#畫原始數據點
plt.axis([-3,3,-5,10])#顯示的時候限制一下取值范圍
plt.legend()
plt.show()

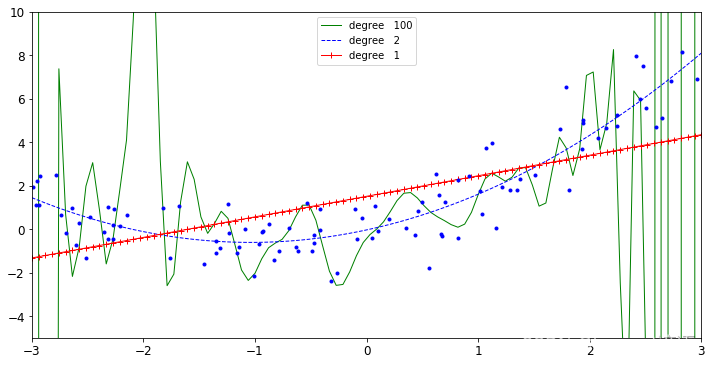
很顯然，綠色函數degree為100，函數很復雜，已經過擬合了，為了盡可能的去滿足所有的點，已經沒必要了。

Ⅱ、不同樣本數量對結果的影響

from sklearn.metrics import mean_squared_error#MSE均方誤差
from sklearn.model_selection import train_test_splitdef plot_learning_curves(model,X,y):X_train, X_val, y_train, y_val = train_test_split(X,y,test_size = 0.2,random_state=100)#測試集20%、訓練集80%、隨機種子為100，也就是每次數據切分都是相同的方式train_errors,val_errors = [],[]#這里沒有使用到測試集，使用了是訓練集和驗證集，保存for m in range(1,len(X_train)):#從1個樣本訓練到使用所有的測試集數據樣本訓練model.fit(X_train[:m],y_train[:m])#訓練y_train_predict = model.predict(X_train[:m])#得出訓練集的結果，依次訓練1個2個直到所有樣本都訓練y_val_predict = model.predict(X_val)#得出驗證集的結果，驗證集選擇全部的，否則不公平train_errors.append(mean_squared_error(y_train[:m],y_train_predict[:m]))#使用m個樣本進行訓練，到時候預測也得是m個val_errors.append(mean_squared_error(y_val,y_val_predict))#使用所有樣本進行驗證，到時候預測個數也得一致plt.plot(np.sqrt(train_errors),'r-+',linewidth = 2,label = 'train_error')plt.plot(np.sqrt(val_errors),'b-',linewidth = 3,label = 'val_error')plt.xlabel('Trainsing set size')plt.ylabel('RMSE')plt.legend()#顯示label

lin_reg = LinearRegression()#線性回歸
plot_learning_curves(lin_reg,X,y)
plt.axis([0,80,0,3.3])#x、y軸取值范圍
plt.show()

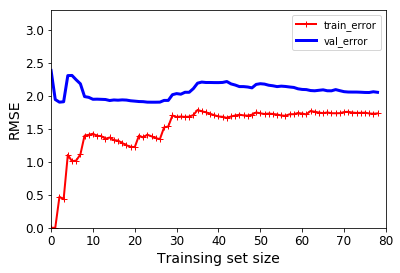
圖中展示的是error，當訓練集樣本數量較少時，訓練集error較小效果較好，但驗證集validation的error較大，兩者的差值較大，效果不好。
數據量越少，訓練集的效果會越好，但是實際測試效果很一般。實際做模型的時候需要參考測試集和驗證集的效果。

Ⅲ、多項式回歸的過擬合風險

當degree 過大，也就是多項式太高，過擬合太嚴重。

polynomial_reg = Pipeline([('poly_features',PolynomialFeatures(degree = 25,include_bias = False)),('lin_reg',LinearRegression())])
plot_learning_curves(polynomial_reg,X,y)
plt.axis([0,80,0,5])
plt.show()

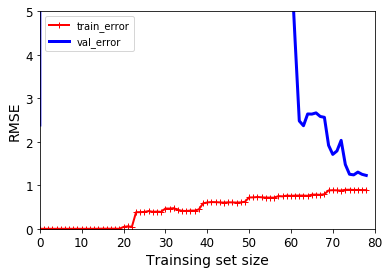
訓練集和驗證集相差太明顯了，可以等價于訓練集為平時的刷題，驗證集為期中期末考試。平常刷題錯誤率很低，最后的期中期末考試卻錯了一塌糊涂，這就是過擬合。

三、正則化

出現過擬合咋辦？正則化專門解決過擬合問題的。
正則化實際上就是對權重參數進行懲罰，讓權重參數盡可能平滑一些，有兩種不同的方法來進行正則化懲罰：

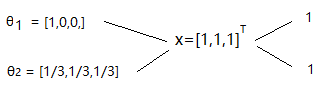
θ1和θ2與x相乘結果都一樣，要你你會選擇哪個？小傻子都知道，會選擇θ2，因為θ2考慮了三個元素，而θ1只考慮了第一個元素。
此時正則化公式就出現了：為了就是對每個θ參數進行選取最優

Ⅰ、嶺回歸

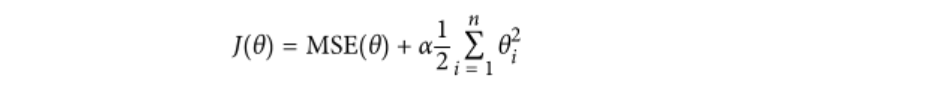
其中J(θ)為損失函數，當然越小越好。前面的均方誤差是一樣的，后面的為整數，越小越好。帶入公式可得，θ2效果最佳。

from sklearn.linear_model import Ridge
np.random.seed(42)#構建隨機種子
m = 20#指定樣本數量
X = 3*np.random.rand(m,1)#x的取值范圍[0,3]之間選取20個點就行了
y = 0.5 * X +np.random.randn(m,1)/1.5 +1#自己定義一個函數方程
X_new = np.linspace(0,3,100).reshape(100,1)#測試數據def plot_model(model_calss,polynomial,alphas,**model_kargs):for alpha,style in zip(alphas,('b-','g--','r:')):#選取多個α值model = model_calss(alpha,**model_kargs)#對model實例化if polynomial:model = Pipeline([('poly_features',PolynomialFeatures(degree = 10,include_bias = False)),('StandardScaler',StandardScaler()),('lin_reg',model)])model.fit(X,y)y_new_regul = model.predict(X_new)#預測一下當前得到的結果lw = 2 if alpha > 0 else 1#指定線條寬度plt.plot(X_new,y_new_regul,style,linewidth = lw,label = 'alpha = {}'.format(alpha))plt.plot(X,y,'b.',linewidth =3)plt.legend()#顯示標簽plt.figure(figsize=(14,6))#設置一個大圖展示
plt.subplot(121)#兩個子圖的第一個
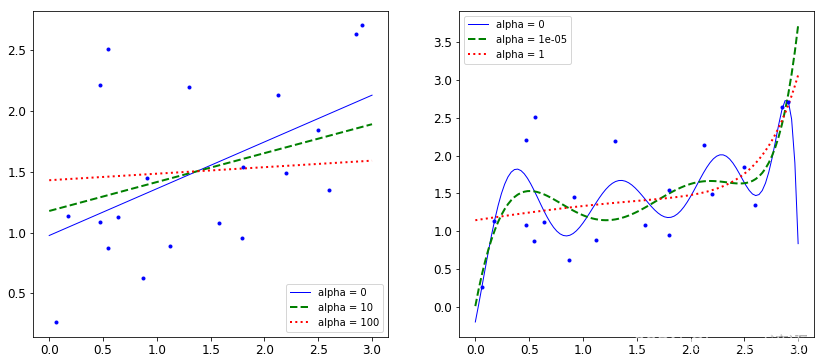
plot_model(Ridge,polynomial=False,alphas = (0,10,100))#不做多項式擬合操作  α的取值表示正則化的程度
plt.subplot(122)#兩個子圖的第二個
plot_model(Ridge,polynomial=True,alphas = (0,10**-5,1))#做多項式擬合操作   α的取值表示正則化的程度
plt.show()

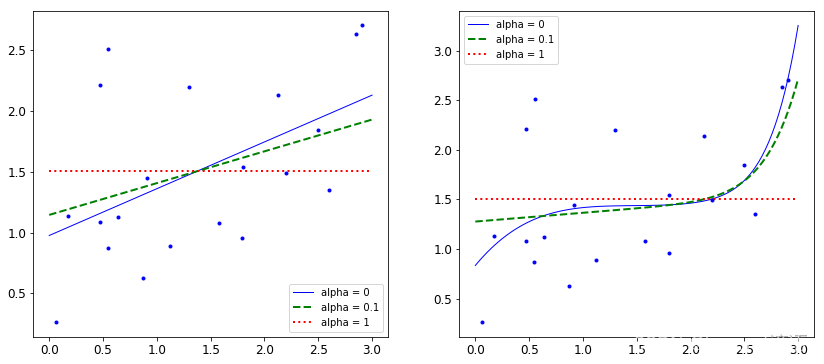
Ⅱ、lasso

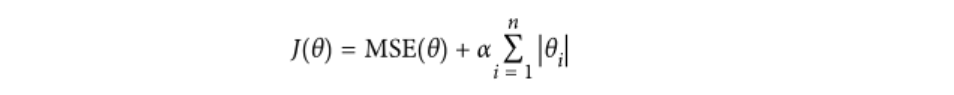
from sklearn.linear_model import Lassoplt.figure(figsize=(14,6))
plt.subplot(121)
plot_model(Lasso,polynomial=False,alphas = (0,0.1,1))
plt.subplot(122)
plot_model(Lasso,polynomial=True,alphas = (0,10**-1,1))
plt.show()