1、leetcode 701. 二叉搜索樹中的插入操作

1、題目

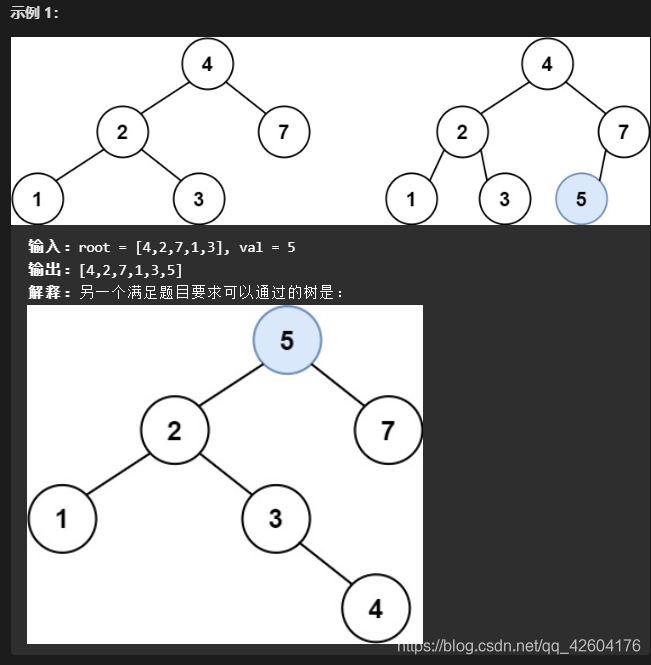
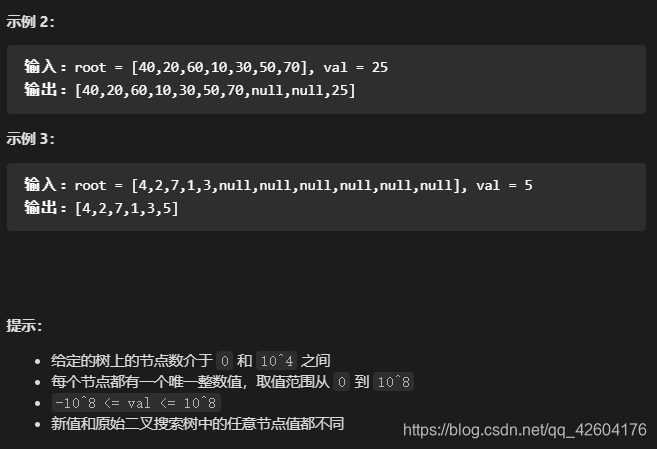
給定二叉搜索樹（BST）的根節點和要插入樹中的值，將值插入二叉搜索樹。 返回插入后二叉搜索樹的根節點。
輸入數據 保證，新值和原始二叉搜索樹中的任意節點值都不同。
注意，可能存在多種有效的插入方式，只要樹在插入后仍保持為二叉搜索樹即可。 你可以返回任意有效的結果 。

2、遞歸法

遞歸返回值以及參數
返回值為空，因為我們進行的是插入操作，不需要知道插在哪兒。
參數：當前結點cur以及需要插入的數值val
終止條件
如果當前指針為空，返回
單層邏輯
首先，按照val的大小，遍歷左右子樹。
如果當前結點的值大于val，且此結點沒有左孩子，則可以將val構造的結點作為其左孩子。
如果當前結點的值小于val，且此結點沒有右孩子，則可以將val構造的結點作為其右孩子。
否則return；
最后在大函數里面返回root就行了。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* cur,int val){if(cur == NULL) return;if(cur->val > val) traversal(cur->left,val);if(cur->val < val) traversal(cur->right,val);if(cur->val > val && cur->left == NULL){//cout<<"插入左結點"<<endl;TreeNode* ans=new TreeNode(val);cur->left = ans;}if(cur->val < val && cur->right == NULL){//cout<<"插入右結點"<<endl;TreeNode* ans=new TreeNode(val);cur->right = ans;}return;}TreeNode* insertIntoBST(TreeNode* root, int val) {if(root == NULL){TreeNode* ans=new TreeNode(val);return ans;} traversal(root,val);return root;}
};

進行了一些修改后的代碼

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* cur,int val){if(cur == NULL) return;cout<<cur->val<<endl;if(cur->val > val){traversal(cur->left,val);if(cur->left == NULL){//cout<<"插入左結點"<<endl;TreeNode* ans=new TreeNode(val);cur->left = ans;}} if(cur->val < val){traversal(cur->right,val);if(cur->right == NULL){//cout<<"插入右結點"<<endl;TreeNode* ans=new TreeNode(val);cur->right = ans;}} return;}TreeNode* insertIntoBST(TreeNode* root, int val) {if(root == NULL){TreeNode* ans=new TreeNode(val);return ans;} traversal(root,val);return root;}
};

3、迭代法

在迭代法遍歷的過程中，需要記錄一下當前遍歷的結點的父結點，這樣才能進行插入結點操作。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if(root == NULL){TreeNode* ans=new TreeNode(val);return ans;} TreeNode* cur = root;TreeNode* parent = root;//記錄上一個結點，否則不挖賦值新結點while(cur != NULL){parent = cur;if(cur->val > val) cur = cur->left;else cur = cur->right;}TreeNode* node = new TreeNode(val);if(val < parent->val) parent->left = node;        //利用parent的結點的值進行賦值else parent->right = node;return root;}
};

2、leetcode 450. 二叉搜索樹中的插入操作

1、題目

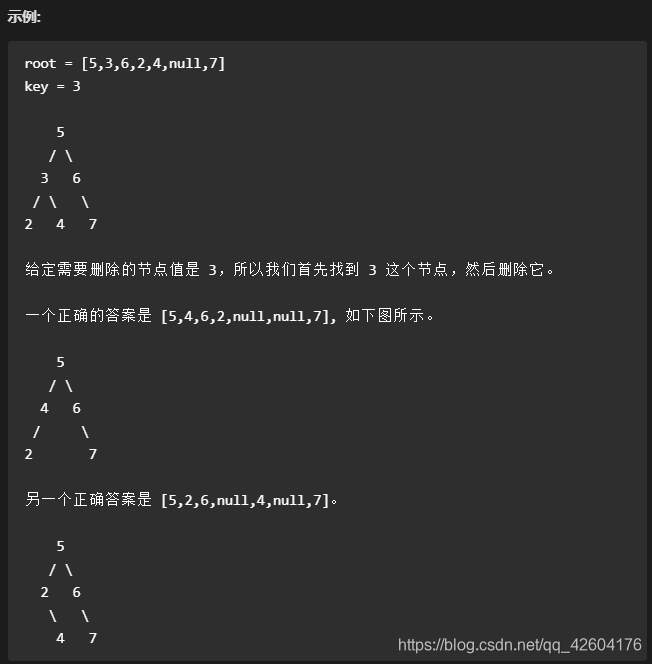
給定一個二叉搜索樹的根節點 root 和一個值 key，刪除二叉搜索樹中的 key 對應的節點，并保證二叉搜索樹的性質不變。返回二叉搜索樹（有可能被更新）的根節點的引用。
一般來說，刪除節點可分為兩個步驟：
首先找到需要刪除的節點；
如果找到了，刪除它。
說明： 要求算法時間復雜度為 O(h)，h 為樹的高度。

2、思路+遞歸法

確定遞歸返回值和參數
通過遞歸返回值來刪除結點。

TreeNode* deleteNode(TreeNode* root, int key)

確定終止條件
遇到空結點返回，說明了沒有找到刪除的結點。

if(root == NULL) return root;

確定單層邏輯
1、沒有找到刪除的結點，遍歷到空結點直接返回。
2、找到了刪除的結點：
【1】如果左右孩子都為空，直接刪除這個結點，返回NULL為根結點
【2】如果左孩子為空，右孩子不為空，刪除結點，右孩子補位，返回右孩子作為根結點
【3】如果右孩子為空，左孩子不為空，刪除結點，左孩子補位，返回左孩子作為根結點
【4】如果左右孩子不為空，則將刪除結點的左子樹的頭結點放到刪除結點的右子樹的最左邊結點的左孩子上，返回刪除結點右孩子，作為新的結點
代表的是中序遍歷序列的下一個節點。即比當前節點大的最小節點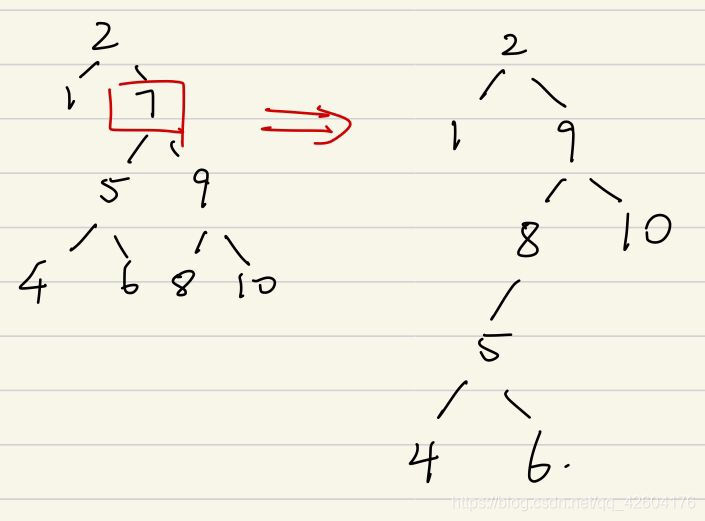

        if(root->val == val){if(!root->left && !root->right) return root;else if(!root->left && root->right) return root->right;else if(root->left && !root->right) return root->left;else {TreeNode* cur = root->right;//找到右子樹的最左邊結點while(cur->left){cur = cur->left;}cur->left = root->left;TreeNode* tmp = root->left;root = root->right;delete tmp;return root;}}

將新的結點返回給上一層，上一層將其作為左或者右孩子：

if(root->val > key) root->left = deleteNode(root->left,key);
if(root->val < key) root->right= deleteNode(root->right,key);

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if(root == NULL) return root;if(root->val == key){if(!root->left && !root->right) return NULL;    //直接刪除結點，返回NULLelse if(!root->left && root->right) return root->right;else if(root->left && !root->right) return root->left;else {TreeNode* cur = root->right;//找到右子樹的最左邊結點while(cur->left){cur = cur->left;}cur->left = root->left;TreeNode* tmp = root;root = root->right;delete tmp;return root;}}if(root->val > key) root->left = deleteNode(root->left,key);if(root->val < key) root->right= deleteNode(root->right,key);return root;}
};

3、迭代法

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* deleteOneNode(TreeNode* target){if(target == NULL) return NULL;if(target->right == NULL) return target->left;//如果right不為空,將left轉移到right左子樹的最左值。TreeNode* cur = target->right;while(cur->left) cur = cur->left;cur->left = target->left;//返回target的右子樹，這樣target結點就被刪除了return target->right;}TreeNode* deleteNode(TreeNode* root, int key) {if(root == NULL) return NULL;TreeNode* cur = root;TreeNode* pre = NULL;       //記錄cur的父結點，用來刪除cur//找到目標結點while(cur){if(cur->val == key) break;pre = cur;if(cur->val > key) cur = cur->left;else cur = cur->right;}if(pre == NULL) return deleteOneNode(cur);      //如果搜索樹只有頭結點//刪除右孩子還是刪除左孩子,cur是父結點的左孩子還是右孩子if(pre->left && pre->left->val == key) pre->left = deleteOneNode(cur);if(pre->right && pre->right->val == key) pre->right = deleteOneNode(cur);return root;}
};

4、刪除結點的兩個方法以及注意點

1、移動樹，找到目標結點直接對指針指向進行改變就結束了
2、覆蓋值，找到目標結點先將目標結點的值和目標結點的右子樹的最左邊的值進行交換；交換后，繼續去遞歸遍歷樹，直到再次遍歷到目標結點的值，此時目標結點已經是葉子結點，左右孩子都為NULL，直接就返回NULL指針，實現了刪除操作。（先覆蓋值，后刪除）
3、刪除一個結點不能簡單地置這個結點為空，我們需要修改父結點對此結點的指向！
例如我們需要將root->right覆蓋掉root，不能root = root->right;而是應該這樣寫;
parent是root的父結點，child可能是左孩子也可能是右孩子，需要按照情況指定。

parent->child =  root->right; 

3、leetcode 669. 修剪二叉搜索樹

1、題目

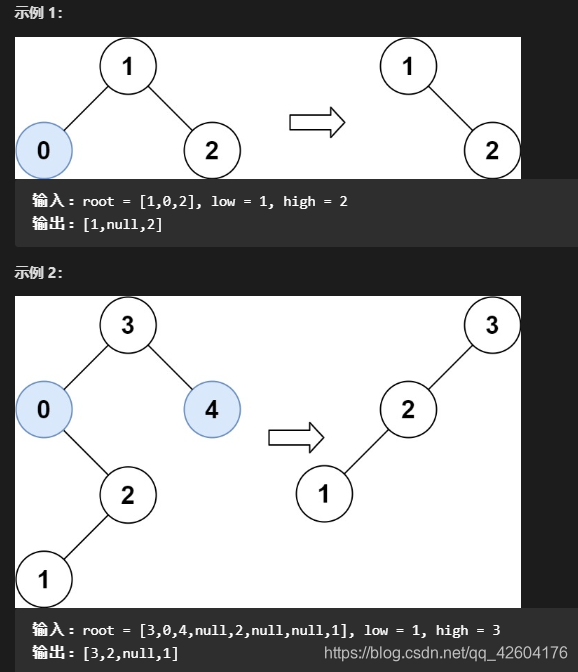
給你二叉搜索樹的根節點 root ，同時給定最小邊界low 和最大邊界 high。通過修剪二叉搜索樹，使得所有節點的值在[low, high]中。修剪樹不應該改變保留在樹中的元素的相對結構（即，如果沒有被移除，原有的父代子代關系都應當保留）。 可以證明，存在唯一的答案。
所以結果應當返回修剪好的二叉搜索樹的新的根節點。注意，根節點可能會根據給定的邊界發生改變。

2、思考與遞歸

因為是要遍歷整棵樹并且做修改，其實不需要返回值也可以，我們也可以完成修剪。但有返回值，更方便，可以通過遞歸函數的返回值來移除結點

如果當前結點的值小于low，要對該結點的右孩子進行再次搜索，直到找到滿足區間的結點或者空結點，最后返回right結點
如果當前結點的值大于high，要對該結點的左孩子進行再次搜索，直到找到滿足區間的結點或者空結點，最后返回left結點。
自上而下遍歷檢查，直到整棵樹遍歷完。
依次遍歷結點左右孩子，并將返回的結果作為當前結點的左右孩子。
最后返回當前結點。
返回的結點必然是val在區間內或者是空結點。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if(root == NULL) return root;if(root->val < low){TreeNode* right = trimBST(root->right,low,high);return right;}if(root->val > high){TreeNode* left = trimBST(root->left,low,high);return left;}root->left = trimBST(root->left,low,high);root->right = trimBST(root->right,low,high);return root;}
};

細致觀察：

root->left = trimBST(root->left,low,high);

用結點3的左孩子把下一層返回的結點0的右孩子(結點2)接住。此時結點3的右孩子就變成了結點2，將結點0從二叉樹中移除了。

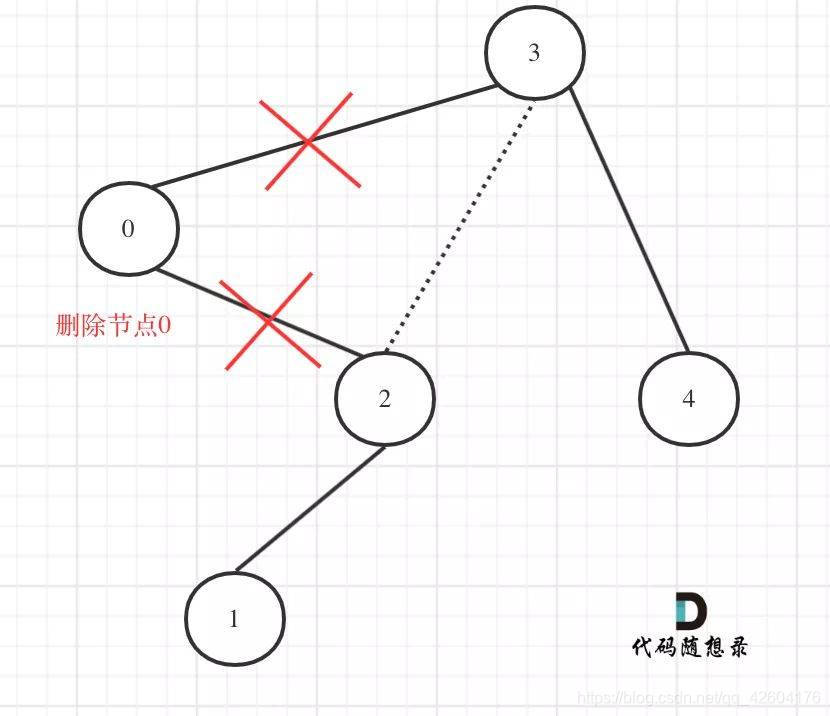
錯誤思路記錄：先得到中序遍歷的結果，然后修剪結果數組，然后通過修剪后的數組構造一個二叉搜索樹.但是這個思路是錯誤的，因為單純用一個中序遍歷數組不能構造出唯一的二叉樹，隨意選擇一種方法會改變二叉樹的結構！
如：low=1,high=3,預期結果應為：

但是我們這樣做的結果是：

3、迭代法

剪枝的三個步驟:
1、將root移動到[L,R]范圍內
2、剪枝左子樹
3、剪枝右子樹
個人認為這個思路比較好理解一點，雖然繁瑣了些。

class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if(root == NULL) return root;//1、處理頭結點，讓root移動到[L,R]范圍內while(root->val < low || root->val > high){if(root->val < low) root = root->right;       //小于L往右走else root = root->left;                     //大于R的往左走}TreeNode* cur = root;//此時root已經在[L,R]范圍內了，處理左孩子元素小于L的情況while(cur){//如果左孩子比low小，就用左孩子的右孩子替代左孩子while(cur->left && cur->left->val < low){cur->left = cur->left->right;}//一直遍歷左孩子cur = cur->left;}cur = root;//此時root'已經在范圍內，處理右孩子元素大于R的情況while(cur){//如果右孩子比high大，就用右孩子的左孩子替代右孩子while(cur->right && cur->right->val > high){cur->right = cur->right->left;}//一直遍歷右孩子cur = cur->right;}return root;}
};

4、leetcode 108. 將有序數組轉換為二叉搜索樹

1、題目

將一個按照升序排列的有序數組，轉換為一棵高度平衡二叉搜索樹。
本題中，一個高度平衡二叉樹是指一個二叉樹每個節點 的左右兩個子樹的高度差的絕對值不超過 1。

利用數組構造二叉樹的本質就是尋找分割點，分割點作為當前結點，然后遞歸左區間和右區間。
有序數組的分割點我們選擇數組中間位置的結點。
如果數組長度為偶數，中間結點有兩個，兩者取其一都可以，所以也就造成了答案不是唯一的。

2、遞歸思路

遞歸返回值以及參數
返回值為結點,我們要用返回值來構造中結點的左右孩子。
參數：數組，分割數組的左邊界、分割數組的右邊界，這里我們定義區間是左閉右閉的。

TreeNode* traversal(vector<int>& nums,int left,int right)

終止條件
由于區間的定義為左閉右閉，所以當left>right時，就是空結點了。

if(left > right) return nullptr;

確定單層邏輯
1、取中間值：int mid = left + ((right - left) / 2);這個是取靠左的中間值這樣可以防止right\left過大時導致的數值越界。
2、以中間位置的元素構造結點：
TreeNode* root = new TreeNode(nums[mid]);
3、劃分區間。root->left接住下一層左區間的構造結點，root->right接住下一層的右區間構造的結點。

int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums,left,mid-1);
root->right = traversal(nums,mid+1,right);

對于數組[-10,-3,0,5,9]觀察遍歷過程：

區間0,4
中間結點0
區間0,1
中間結點-10
區間0,-1
中間結點NULL
區間1,1
中間結點-3
區間1,0
中間結點NULL
區間2,1
中間結點NULL
區間3,4
中間結點5
區間3,2
中間結點NULL
區間4,4
中間結點9
區間4,3
中間結點NULL
區間5,4
中間結點NULL

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:TreeNode* traversal(vector<int>& nums,int left,int right){cout<<"區間"<<left<<","<<right<<endl;if(left > right){cout<<"中間結點"<<"NULL"<<endl;return nullptr;}int mid = left + ((right - left) / 2);cout<<"中間結點"<<nums[mid]<<endl;TreeNode* root = new TreeNode(nums[mid]);root->left = traversal(nums,left,mid-1);root->right = traversal(nums,mid+1,right);return root;}TreeNode* sortedArrayToBST(vector<int>& nums) {TreeNode* root = traversal(nums,0,nums.size()-1);return root;}
};