模擬退火算法解決np
P問題 (P Problems)
P is the set of all the decision problems solvable by deterministic algorithms in polynomial time.
P是多項式時間內確定性算法可解決的所有決策問題的集合。
NP問題 (NP Problems)
NP is the set of all the decision problems that are solvable by non - deterministic algorithms in polynomial time.
NP是可由多項式時間內的非確定性算法解決的所有決策問題的集合。
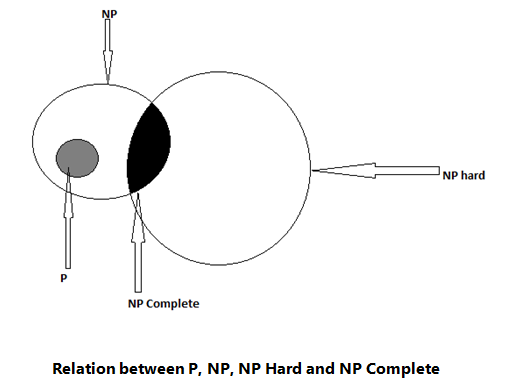
Since deterministic algorithms are just the special case of non - deterministic ones, so we can conclude that P is the subset of NP.
由于確定性算法只是非確定性算法的特例,因此我們可以得出結論,P是NP的子集。
Relation between P and NP
P和NP之間的關系
NP難題 (NP Hard Problem)
A problem L is the NP hard if and only if satisfiability reduces to L. A problem is NP complete if and only if L is the NP hard and L belongs to NP.
當且僅當可滿足性降低到L時,問題L才是NP難。只有當L是NP難且L屬于NP時,問題NP才是完整的。
Only a decision problem can be NP complete. However, an optimization problem may be the NP hard. Furthermore if L1 is a decision problem and L2 an optimization problem, then it is possible that L1 α L2. One can trivially show that the knapsack decision problem reduces to knapsack optimization problem. For the clique problem one can easily show that the clique decision problem reduces to the clique optimization problem. In fact, one can also show that these optimization problems reduce to their corresponding decision problems.
只有決策問題才能完成NP。 但是,優化問題可能是NP難題。 此外,如果L1是決策問題,L2是優化問題,則L1αL2是可能的。 可以簡單地表明,背包決策問題可以簡化為背包優化問題。 對于群體問題,可以很容易地表明,群體決策問題可以簡化為群體優化問題。 實際上,還可以證明這些優化問題可以簡化為相應的決策問題。
NP完整性問題 (NP Completeness Problem)
Polynomial time reductions provide a formal means for showing that one problem is at least as hard as another, within a polynomial time factor. This means, if L1 <= L2, then L1 is not more than a polynomial factor harder than L2. Which is why the “less than or equal to” notation for reduction is mnemonic. NP complete are the problems whose status are unknown.
多項式時間縮減提供了一種形式化的方法,用于顯示在多項式時間因子內一個問題至少與另一個問題一樣困難。 這意味著,如果L1 <= L2,則L1不大于比L2難的多項式因數。 這就是為什么“小于或等于”減少表示法是助記符的原因。 NP完全是狀態未知的問題。
Some of the examples of NP complete problems are:
NP完全問題的一些示例是:
1. Travelling Salesman Problem:
1. 旅行商問題 :
Given n cities, the distance between them and a number D, does exist a tor programme for a salesman to visit all the cities so that the total distance travelled is at most D.
給定n個城市,它們之間的距離與數字D確實存在一個推銷員計劃,以供銷售人員訪問所有城市,這樣總行駛距離最多為D。
2. Zero One Programming Problem:
2.零編程問題:
Given m simultaneous equations,
給定m個聯立方程,
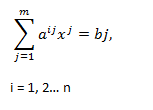
3. Satisfiability Problem:
3.滿意度問題:
Given a formula that involves propositional variables and logical connectives.
給定一個涉及命題變量和邏輯連接詞的公式。
A language L is the subset [0, 1]* is NP complete if,
語言L是子集[0,1] *是NP完整,如果,
L belongs to NP and
L屬于NP
L' ← L for every L' belongs to NP
L'←L每L'都屬于NP
All NP complete problems are NP hard, but some NP hard problems are not known to be NP complete.
所有的NP完全問題都是NP困難的,但是某些NP困難問題并不是NP完全的。
If NP hard problems can be solved in polynomial time, then all the NP complete problems can be solved in polynomial time.
如果NP難題可以在多項式時間內解決,那么所有NP完全問題都可以在多項式時間內解決。
翻譯自: https://www.includehelp.com/algorithms/p-and-np-problems.aspx
模擬退火算法解決np



















