一、聚類概念
1，通俗易懂而言，聚類主要運用于無監督學習中，也就是將沒有標簽的東西如何分為幾堆兒。
2，無監督學習即沒有標簽，不知道這些玩意到底是啥。當然，有監督學習就是由標簽，我們是提前知道這些玩意是啥。
3，聚類問題存在的問題難點：你咋知道這些玩意兒是一類？怕啥？你通過啥進行判斷分類的？也就是如何評估和如何調參問題。
二、K-MEANS算法
Ⅰ，基本概念
1，需要得到簇的個數，即需要指定K值。需要劃分多少類。
2，質心：均值，即向量各維取平均。例如五個點，其質心坐標為((x1+x2+x3+x4+x5)/5,(y1+y2+y3+y4+y5)/5)
3，距離的度量：常用歐幾里得距離和余弦相似度（先標準化）
4，優化目標：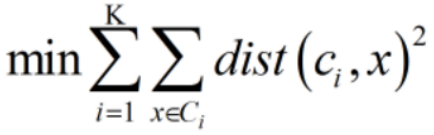
，求出每個點到哪個質心距離最近
Ⅱ，算法思路
①首先取得一些數據點
②假設K設置成2，隨便找取兩個初始化點
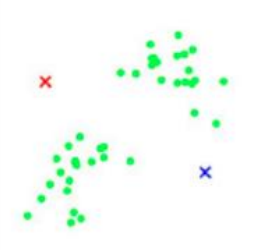
③開始迭代所有的綠色點，看看離哪個質心(紅色還是藍色)最近，離誰近就跟誰一個簇
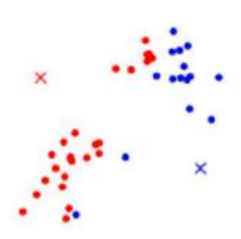
④把所有紅色和藍色的點全部取出來，求取質心，重新獲取質心，更新質心參數
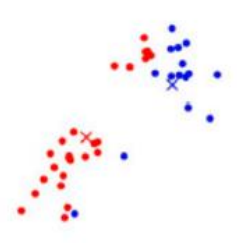
⑤重新對所有的數據進行求取離哪個質心最近就跟哪個質心為同一簇
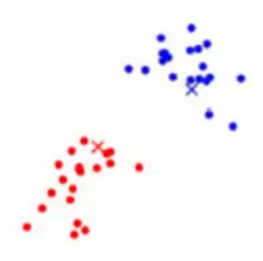
⑥繼續將所有的紅色和藍色點再次分別求取質心，再對所有點進行遍歷，看離哪個質心距離近就和哪個質心為同一簇
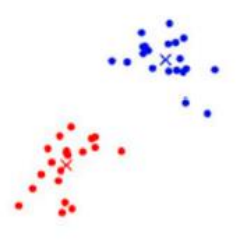
⑦再次將所有的紅色和藍色點分別求取質心，再次遍歷所有點，找離哪個質心最近歸為一簇，直到所有的點歸屬簇不再發生變動為止
Ⅲ，優劣勢
優點：簡單、快速、適合一般情況下的常規數據集
缺點：K值不容易確定、復雜度和樣本呈線性關系、很難發現任意形狀的簇
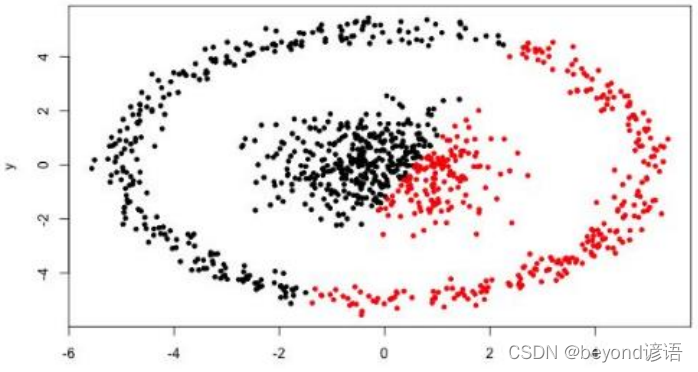
Ⅳ，K-Means可視化展示
K-Means可視化展示網站
三、DBSCAN算法
Ⅰ，基本概念
DBSCAN，Density-Based Spatial Clustering of Applications with Noise
畫圈--->找點--->發展下線開始洗腦
1，核心對象：若某個點的密度達到算法設定的閾值則其為核心點。即 r 鄰域內點的數量不小于 minPts
2，?-鄰域的距離閾值：設定的半徑r
3，直接密度可達：若某點p在點q的 r 鄰域內，且q是核心點則p-q直接密度可達。
4，密度可達：若有一個點的序列q0、q1、…qk，對任意q(i)—q(i-1)是直接密度可達的 ，則稱從q0到qk密度可達，這實際上是直接密度可達的“傳播”。
5，密度相連：若從某核心點p出發，點q和點k都是密度可達的 ,則稱點q和點k是密度相連的。
6，邊界點:屬于某一個類的非核心點,不能發展下線了
7，噪聲點：不屬于任何一個類簇的點，從任何一個核心點出發都是密度不可達的
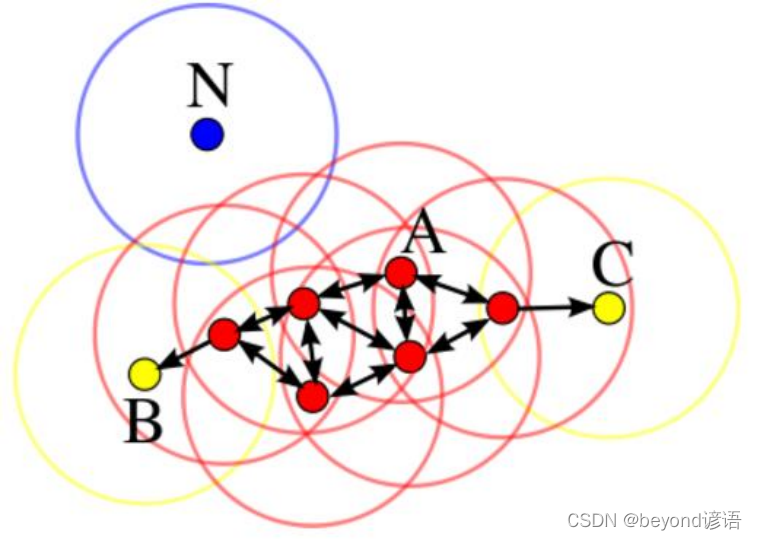
A：核心對象、B,C：邊界點、N：離群點
Ⅱ，算法思路
①輸入參數D，即你的數據集
輸入參數?，即指定半徑
輸入參數MinPts，密度閾值，也就是畫出來的圈內最少得有這么多點才行
②參數選擇
1，半徑?，可以根據K距離來設定：找突變點K距離：給定數據集P={p(i); i=0,1,…n}，計算點P(i)到集合D的子集S中所有點之間的距離，距離按照從小到大的順序排序，d(k)就被稱為k-距離。
2，MinPts： k-距離中k的值，一般取的小一些，多次嘗試
Ⅲ，優劣勢
優勢：不需要指定簇個數、可以發現任意形狀的簇、擅長找到離群點（檢測任務）、兩個參數就夠了
劣勢：高維數據有些困難（可以做降維）、參數難以選擇（參數對結果的影響非常大）、Sklearn中效率很慢（數據削減策略）
Ⅳ，DBSCAN可視化展示
DBSCAN可視化展示網站
