題目

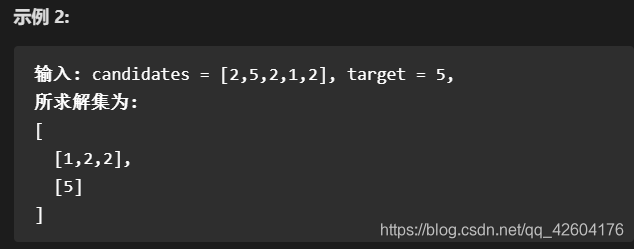
給定一個數組 candidates 和一個目標數 target ，找出 candidates 中所有可以使數字和為 target 的組合。
candidates 中的每個數字在每個組合中只能使用一次。

思考以及代碼

如果我們直接套用39題的思路，那么就會出現重復的組合。

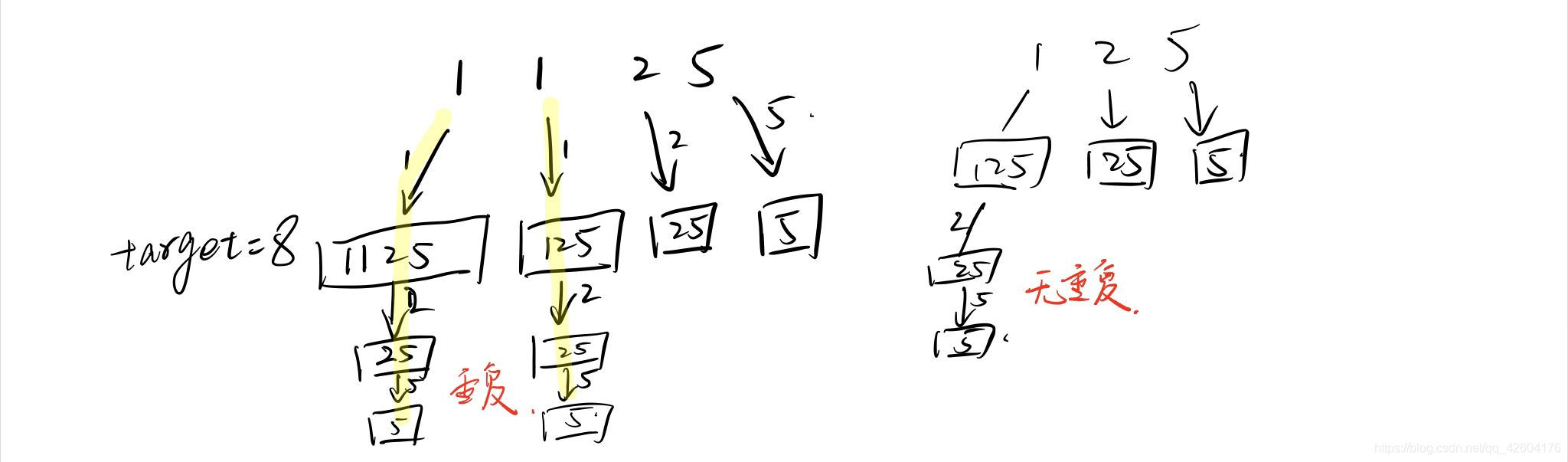
重復組合的產生，是因為集合中有重復的元素。
去重，就是使用過的元素不能重復選取。
我們result的重復組合的產生肯定是和重復元素有關的，我們從解空間樹的深度(遞歸調用)和寬度(for循環)來看：
1、元素的重復的影響可能出現在在解空間樹的寬度和深度上。
2、寬度上的重復決定了我們result解的組合的重復，深度上的重復決定了result解的每個子結果res的元素重復。
3、結合題意：如果是在寬度上重復我們需要去除，如果是在深度上重復我們不需要去除。

在寬度上進行去重所以我們在for循環的過程中加入限制。

//如果遇到同一個集合的重復元素，跳過這個元素即可
if(i > startindex && candidates[i] == candidates[i-1]) continue;

注意這里我們已經對原數組進行排序了，所以重復的元素一定靠在一起

class Solution {
public:vector<vector<int>> result;vector<int> res;int sum;void clear_solution_param(){result.clear();res.clear();sum=0;}void backtracking(vector<int>& candidates,int startindex,int n){   if(sum > n) return;if(sum == n){result.push_back(res);return;}for(int i=startindex;i<candidates.size();i++){//由于輸入的數組是有序的，所以直接進行剪枝。如果sum加上這個集合元素大于目標，此層就不需要往后看了，因為后面的元素加上sum肯定大于目標if(sum+candidates[i]>n) break;//如果遇到同一個集合的重復元素，跳過這個元素即可if(i > startindex && candidates[i] == candidates[i-1]) continue;//處理結點；res.push_back(candidates[i]);sum+=candidates[i];//遞歸,探索下一層backtracking(candidates,i+1,n);		//遞歸sum-=candidates[i];//回溯，撤銷處理結果res.pop_back();}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {clear_solution_param();//排序加速剪枝sort(candidates.begin(),candidates.end());backtracking(candidates,0,target);return result;}
};