一、回歸

可以拿正態分布為例，比如身高，若平均身高為1.78m，絕大多數人都是1.78m左右，超過2m的很少，低于1m的也不多。
很多事情都會回歸到一定的區間之內，即回歸到平均值。

機器學習沒有完美解，只有最優解。
機器學習的目的就是要以最快的速度，找到誤差最小的那個最優解。

二、線性回歸

線性：一次方關系，y=a+b*x，各點連接可以形成一條直線。
線性即量與量之間按比例、呈直線的關系，在空間和時間上代表規則和光滑的運動。
x是影響y的因素或維度
總結起來：線性回歸就是①數據y和x呈一次方關系、②數據中的每條記錄都符合正態分布

三、最小二乘法

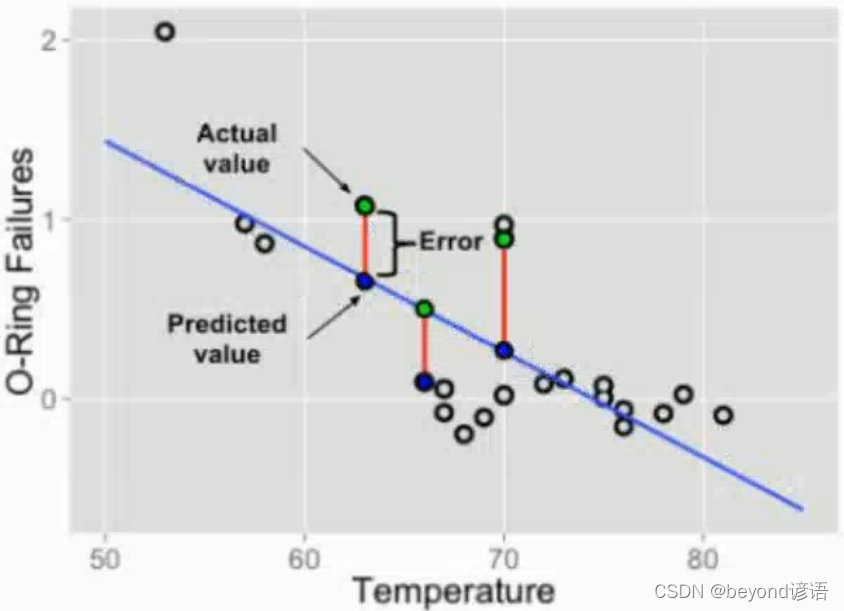
例如：y = a * x + b，(x1,y1)，(x2,y2)，(x3,y3)，(x4,y4)，因為是一元一次函數，其實只需要兩個點就可以確定出a和b的值，但實際上會有很多的數據點，此時就需要兩兩組合，分別求出a和b的值，對應不同的a和b求得的y’值是不相同的，分別代入損失函數中去，求得損失函數的值，找取最小的a和b的值，即為最優解，該a和b參數就是我們要求的最優解。

假設有m個樣本點，y’為直線上的點，y為真實點的位置，一個樣本誤差為y’-y。
通常把損失函數loss定義為：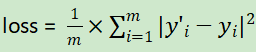
我們的目的就是盡可能使得loss損失函數值最小，找到那個最優參數a和b。

四、多元線性回歸

現實生活中，對數據的分析不可能僅僅一個自變量，絕大多數情況都是多個自變量進行分析。
多元線性也就是多元一次函數。本質就是算法(公式)變換為了多元一次方程組。一般來講W和X都是n維列向量。
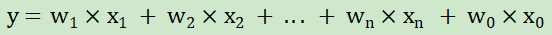，一般情況下x0恒為1，目的是方便轉換為矩陣進行求解。

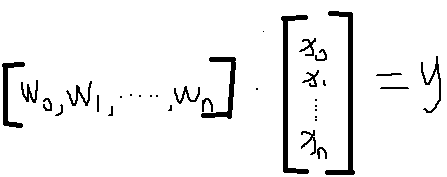，其中x1，x2…xn表示n個樣本點。
也常表示為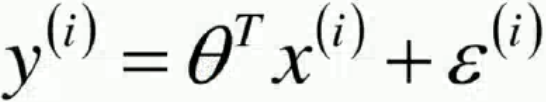：，其中ε為誤差就等價于隨機變量，θ就是W，y表示真實值，θTx為預測值。真實值=預測值+誤差。

五、最大似然估計

最大似然估計是一種統計方法，它用來求一個樣本集的相關概率密度函數的參數。
似然likelihood，也就是可能性，與probabilite概率的同義詞可以互換。

六、中心極限定理

中心極限定理是概率論中討論隨機變量序列部分和分布漸進于正態分布的一類定理。
這組定理是數理統計和誤差分析的理論基礎，指出了大量隨機變量積累分布函數逐點收斂到正態分布的積累分布函數的條件。
它是概率論中最重要的一類定理，有廣泛的實際應用背景。在自然界與生產中，一些現象受到許多相互獨立的隨機因素的影響，如果每個因素所產生的影響都很微小時，總的影響可以看作是服從正態分布的。中心極限定理就是從數學上證明了這一現象。

七、誤差

第i個樣本實際的值(y) = 預測的值(y’) + 誤差(ε)
假定所有的樣本都是獨立的，有上下的震蕩，震蕩認為是隨機變量，足夠多的隨機變量疊加之后形成的分布，根據中心極限定理，它服從的就是正態分布，因為它是正常狀態下的分布，也就是高斯分布。均值和方差都是某個具體的值。
既然誤差符合均值為0，方差為平方的正態分布，那么就可以把它的概率密度函數給寫出來。

八、概率密度函數

最簡單的概率密度函數是均勻分布的密度函數。
最簡單的概率密度函數是均勻分布的 密度函數，也就是說，當x不在[a,b]上的時候，函數值等于0；而在區間[a,b]上的時候，函數值等于這個函數。這個函數并不是完全的連續函數，但是它是可積函數。

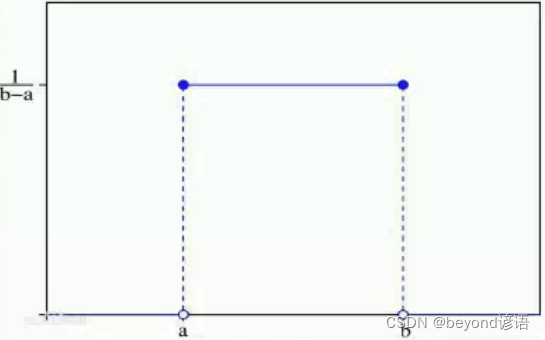
正態分布是重要的概率分布，它的概率密度函數是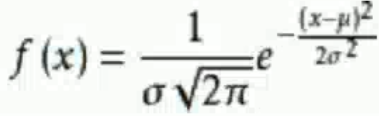：，隨著參數μ和σ的變化，概率分布也產生變化。

真實值 = 預測值 + 誤差，ε誤差等價于隨機變量，目的是用ε代替(x-μ)。
把公式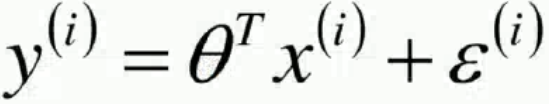代入上述概率密度函數中得：
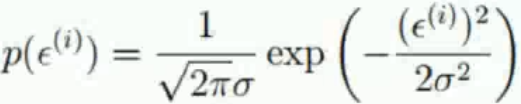，求得第i個樣本的概率密度。
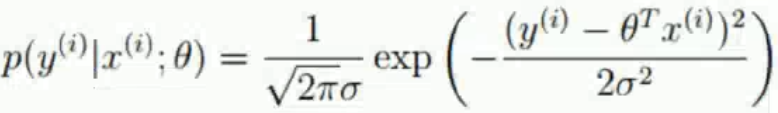，把誤差ε用表達式代替，得出第i個樣本的最大似然估計函數。

概率密度不等于概率，但是概率密度跟概率是等價的。就類似 你不知這個人的體型，但是你知道他穿的衣服的長度等信息。
上述為一個樣本的概率密度，要求所有樣本的概率密度即：
最大總似然估計函數(likelihood)：

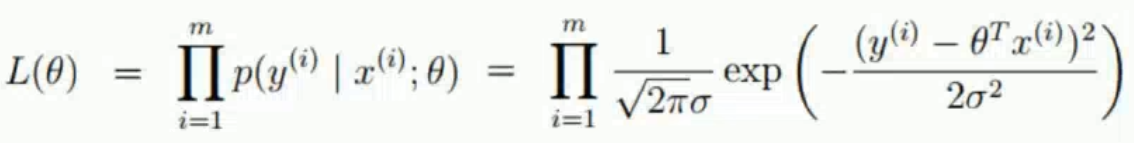
連乘確實優點麻煩，故想到了通過對數函數運行進行轉換為連加。

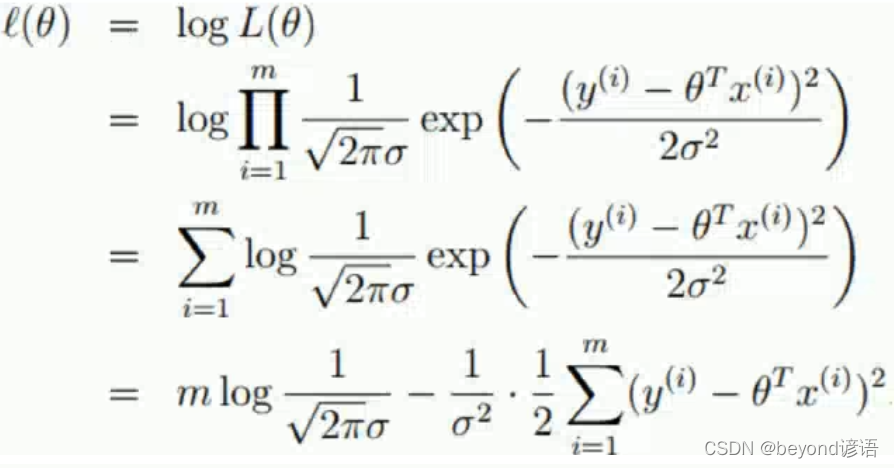
前半部分是個常數，為了簡化操作，將后半部分提出來，形成一個新的目標函數。
最終得到目標函數：

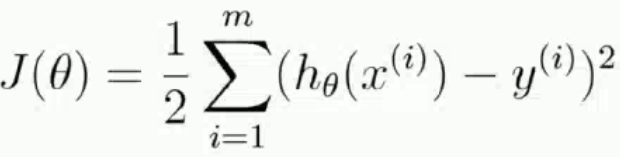
要求L(θ)最大，即等價于求解J(θ)最小，我們關系的不是J(θ)，我們要找的只是θ取何值，J(θ)最小，關心的是θ！

九、總結

Ⅰ為什么求總似然的時候，要用正態分布的概率密度函數？
答：因為中心極限定理可以得知，如果假設樣本之間是獨立事件，誤差變量隨機產生，那么它就服從正態分布。

Ⅱ總似然不是概率相乘嗎？為什么用概率密度函數進行相乘？
答：因為概率不好求，所以當找到概率密度相乘最大的時候，就相當于找到了概率相乘最大的時候。

Ⅲ概率為什么不好求？
答：概率在正態分布中表示的時候面積，面積需要積分，然而我們的樣本都是離散的點，故真正的面積是無法積分出來的，即概率不好求。

Ⅳ總似然最大和最優解有啥關系？
答：當找到可以使得總似然最大的條件，也就可以找到DataSet數據集最吻合某個正態分布，即找到了最優解。