一、梯度下降法(GD，Gradient Descent)

Ⅰ、得到目標函數J(θ)，求解使得J(θ)最小時的θ值

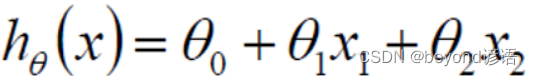
在這里插入圖片描述
當然，這里只是取了倆特征而已，實際上會有m個特征維度

通過最小二乘法求目標函數最小值
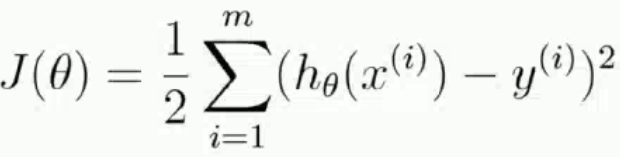
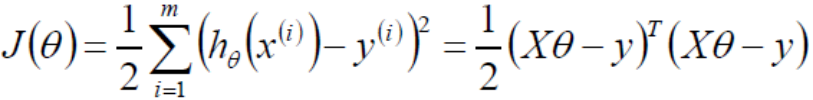
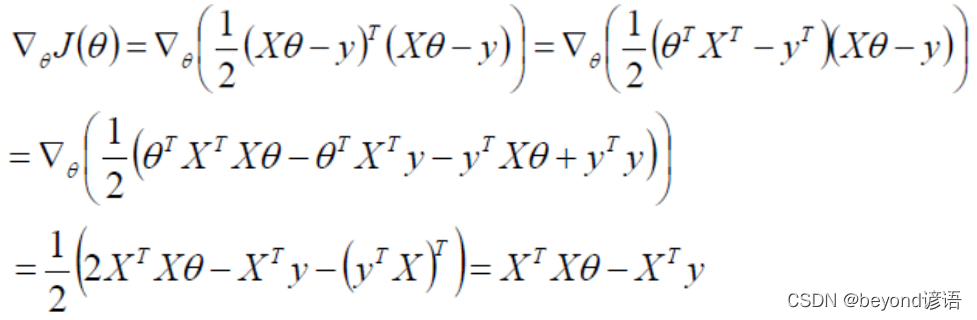
在這里插入圖片描述

令偏導為0即可求解出最小的θ值，即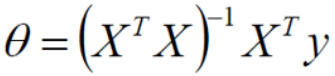

Ⅱ、判定為凸函數

凸函數有需要判斷方法，比如：定義、一階條件、二階條件等。利用正定性判定使用的是二階條件。
半正定一定是凸函數，開口朝上，半正定一定有極小值
在用二階條件進行判定的時候，需要得到Hessian矩陣，根據Hessian的正定性判定函數的凹凸性。比如Hessian矩陣半正定，函數為凸函數；Hessian矩陣正定，函數為嚴格凸函數

Hessian矩陣：黑塞矩陣(Hessian Matrix)，又稱為海森矩陣、海瑟矩陣、海塞矩陣等，是一個多元函數的二階偏導數構成的方陣，描述了函數的局部曲率。

Ⅲ、Hessian矩陣

黑塞矩陣是由目標函數在點x處的二階偏導數組成的對稱矩陣
正定：對A的特征值全為正數，那么A一定是正定的
不正當：非正定或半正定
若A的特征值≥0，則半正定，否則，A為非正定。

對J(θ)損失函數求二階導，之后得到的一定是半正定的，因為自己和自己做點乘。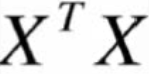在這里插入圖片描述

Ⅳ、解析解

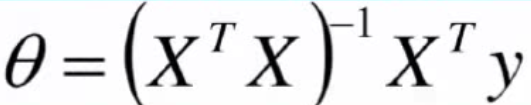
在這里插入圖片描述
數值解是在一定條件下通過某種近似計算得出來的一個數值，能在給定的精度條件下滿足方程，解析解為方程的解析式(比如求根公式之類的)，是方程的精確解，能在任意精度下滿足方程。

Ⅴ、梯度下降法

這個課程跟其他課程講的差不多，這里我就不再贅述了。梯度下降法

梯度下降法：是一種以最快的速度找到最優解的方法。

流程：
1，初始化θ，這里的θ是一組參數，初始化也就是random一下即可
2，求解梯度gradient
3，θ(t+1) = θ(t) - grand*learning_rate
這里的learning_rate常用α表示學習率，是個超參數，太大的話，步子太大容易來回震蕩；太小的話，迭代次數很多，耗時。
4，grad < threshold時，迭代停止，收斂，其中threshold也是個超參數
超參數：需要用戶傳入的參數，若不傳使用默認的參數。

Ⅵ、代碼實現

導包

import numpy as np
import matplotlib.pyplot as plt

初始化樣本數據

# 這里相當于是隨機X維度X1，rand是隨機均勻分布
X = 2 * np.random.rand(100, 1)

# 人為的設置真實的Y一列，np.random.randn(100, 1)是設置error，randn是標準正太分布
y = 4 + 3 * X + np.random.randn(100, 1)

# 整合X0和X1
X_b = np.c_[np.ones((100, 1)), X]
print(X_b)
"""
[[1.         1.01134124][1.         0.98400529][1.         1.69201204][1.         0.70020158][1.         0.1160646 ][1.         0.42502983][1.         1.90699898][1.         0.54715372][1.         0.73002827][1.         1.29651341][1.         1.62559406][1.         1.61745598][1.         1.86701453][1.         1.20449051][1.         1.97722538][1.         0.5063885 ][1.         1.61769812][1.         0.63034575][1.         1.98271789][1.         1.17275471][1.         0.14718811][1.         0.94934555][1.         0.69871645][1.         1.22897542][1.         0.59516153][1.         1.19071408][1.         1.18316576][1.         0.03684612][1.         0.3147711 ][1.         1.07570897][1.         1.27796797][1.         1.43159157][1.         0.71388871][1.         0.81642577][1.         1.68275133][1.         0.53735427][1.         1.44912342][1.         0.10624546][1.         1.14697422][1.         1.35930391][1.         0.73655224][1.         1.08512154][1.         0.91499434][1.         0.62176609][1.         1.60077283][1.         0.25995875][1.         0.3119241 ][1.         0.25099575][1.         0.93227026][1.         0.85510054][1.         1.5681651 ][1.         0.49828274][1.         0.14520117][1.         1.61801978][1.         1.08275593][1.         0.53545855][1.         1.48276384][1.         1.19092276][1.         0.19209144][1.         1.91535667][1.         1.94012402][1.         1.27952383][1.         1.23557691][1.         0.9941706 ][1.         1.04642378][1.         1.02114013][1.         1.13222297][1.         0.5126448 ][1.         1.22900735][1.         1.49631537][1.         0.82234995][1.         1.24810189][1.         0.67549922][1.         1.72536141][1.         0.15290908][1.         0.17069838][1.         0.27173192][1.         0.09084242][1.         0.13085313][1.         1.72356775][1.         1.65718819][1.         1.7877667 ][1.         1.70736708][1.         0.8037657 ][1.         0.5386607 ][1.         0.59842584][1.         0.4433115 ][1.         0.11305317][1.         0.15295053][1.         1.81369029][1.         1.72434082][1.         1.08908323][1.         1.65763828][1.         0.75378952][1.         1.61262625][1.         0.37017158][1.         1.12323188][1.         0.22165802][1.         1.69647343][1.         1.66041812]]
"""

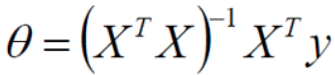
在這里插入圖片描述

# 常規等式求解theta
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(theta_best)
"""
[[3.9942692 ][3.01839793]]
"""

# 創建測試集里面的X1
X_new = np.array([[0], [2]]) 
X_new_b = np.c_[(np.ones((2, 1))), X_new]
print(X_new_b)
y_predict = X_new_b.dot(theta_best)
print(y_predict)
"""
[[1. 0.][1. 2.]]
[[ 3.9942692 ][10.03106506]]
"""

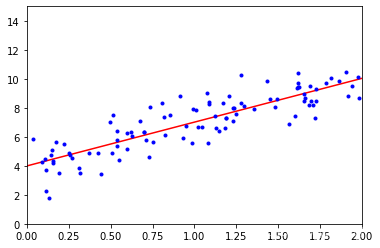
繪圖

plt.plot(X_new, y_predict, 'r-')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 15])
plt.show()

在這里插入圖片描述

Ⅶ、完整代碼

import numpy as np
import matplotlib.pyplot as plt# 這里相當于是隨機X維度X1，rand是隨機均勻分布
X = 2 * np.random.rand(100, 1)
# 人為的設置真實的Y一列，np.random.randn(100, 1)是設置error，randn是標準正太分布
y = 4 + 3 * X + np.random.randn(100, 1)# 整合X0和X1
X_b = np.c_[np.ones((100, 1)), X]
print(X_b)# 常規等式求解theta
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(theta_best)# 創建測試集里面的X1
X_new = np.array([[0], [2]]) 
X_new_b = np.c_[(np.ones((2, 1))), X_new]
print(X_new_b)
y_predict = X_new_b.dot(theta_best)
print(y_predict)#繪圖
plt.plot(X_new, y_predict, 'r-')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 15])
plt.show()

二、批量梯度下降法(BGD，Batch Gradient Descent)

Ⅰ、梯度下降法流程

梯度下降法流程：
1，初始化theta，w0…wn
2，接著求梯度gradient
3，theta_t+1 = theta_t - grad * learning_rate
learning_rate是個超參數，太大容易來回振蕩，太小步子太短，需要走很長時間，不管太大還是太小，
都會迭代次數很多，耗時很長
4，等待grad < threshold，迭代停止，收斂，threshold是個超參數

推導線性回歸的loss function的導函數，目的是可以更快的求解梯度！
grad_j = (1/m) * (Xj)^Transpose * (Xtheta - y)
grads = (1/m) * X^Transpose * (Xtheta - y)

上面就是批量梯度下降的時候，去求解gradients梯度的公式！
不管是批量梯度下降，還是隨機梯度下降，流程里面的1，3，4都是一樣的，只有第二步求梯度稍有不同！
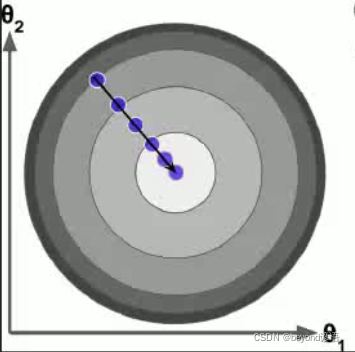
在這里插入圖片描述

Ⅱ、批量梯度下降法(BGF)

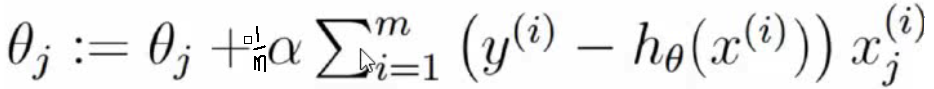
在這里插入圖片描述
初始化W，隨機W，進行賦初始值
沿著負梯度方向迭代，更新后的W使得J(W)更小

Ⅲ、完整代碼

import numpy as npX = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
# print(X_b)learning_rate = 0.1
n_iterations = 10000
m = 100# 1，初始化theta，w0...wn
theta = np.random.randn(2, 1)
count = 0# 4，不會設置閾值，之間設置超參數，迭代次數，迭代次數到了，我們就認為收斂了
for iteration in range(n_iterations):count += 1# 2，接著求梯度gradientgradients = 1/m * X_b.T.dot(X_b.dot(theta)-y)# 3，應用公式調整theta值，theta_t + 1 = theta_t - grad * learning_ratetheta = theta - learning_rate * gradientsprint(count)
print(theta)

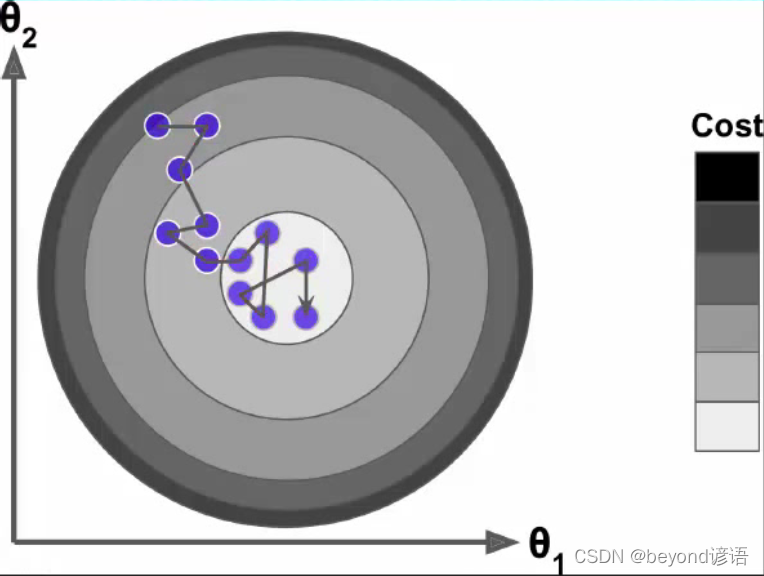
三、隨機梯度下降法(SGD，Stochastic Gradient Descent)

批量梯度下降法中考慮了所有的樣本的梯度，找到最優梯度然后再往下走，很慢。
隨機梯度下降則從所有的樣本中隨機找一個樣本的梯度，然后按這個梯度向下走
在這里插入圖片描述

完整代碼

import numpy as npdef learning_schedule(t):#隨著迭代次數的增加，會相應的減小學習率return t0 / (t+t1)X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
# print(X_b)n_epoches = 500
t0,t1 = 5,50#超參數m = 100
theta = np.random.randn(2,1)#隨機初始化θ值for epoch in range(n_epoches):#執行500次迭代for i in range(m):random_index = np.random.randint(m)#從m個樣本中隨機抽取一個，作為索引xi = X_b[random_index:random_index+1]#根據索引取出值yi = y[random_index:random_index+1]gradients = 2*xi.T.dot(xi.dot(theta)-yi)#得到梯度learning_rate = learning_schedule(epoch*m+i)#隨著迭代次數的增加，會相應的減小學習率theta = theta - learning_rate * gradients#根據梯度下降公式調整θprint(theta)

上面代碼里面除了隨機抽取一條數據來求解梯度，還隨著迭代次數的增多，不斷減小learning_rate，最終減小步長！

總結

Ⅰ隨機梯度下降，怎么隨機的呢？
答：其實就是在求梯度的時候，不再用所有的m個樣本數據來計算，而是隨機的選擇一條數據來計算梯度！

Ⅱ隨機梯度下降的好處是什么？缺點是什么？
答：在求梯度的時候快，迭代次數有可能更多，最終可能落不到全局最優解上

ⅢMini-Batch GD是什么？
答：就是在求梯度的時候做了一個折中，不用所有的數據，而是隨機選擇一部分數據來求梯度！

Ⅳ為什么要不斷的調整步長？
答：就是為了讓越接近最優解的時候，調整的幅度越小，避免來回震蕩！

Ⅴ如果我們不人為的調小步長，會不會隨著迭代的次數增多，調整的幅度自動減小？
答：調整的幅度取決于誰？取決于學習率和梯度，梯度事實上越接近最優解，梯度的絕對值越小

四、小批量梯度下降法(MBGD，Mini-Batch Gradient Descent)

隨機梯度下降法是隨機抽取一個樣本的梯度作為整體梯度進行下降，速度上去了，但是樣本的隨機選取很容易抽到不好的樣本導致最終的結果偏差很大。批量梯度下降法考慮了所有樣本的梯度，選擇最優，但是速度太慢。
小批量梯度下降法隨機選取一小部分樣本的梯度，選擇其中最優的解作為最終的梯度。隨著迭代次數的增加學習率會降低，步長減小。