目錄

• • C++03的左值和右值
  • C++11的左值和右值
  • 將亡值

在C++03中就有相關的概念

C++03的左值和右值

通俗的理解：

(1) 能放在等號左邊的是lvalue
(2) 只能放在等號右邊的是rvalue
(3) lvalue可以作為rvalue使用

對于第三點可以舉個例子：
int x ;
x = 6; //x是左值，6是右值
int y ;
y = 6; //y是左值，6是右值
y = x; //x作為右值，所以左值是可以作為右值使用的

C++11對左值和右值做出了更加詳細的劃分。

C++11的左值和右值

表達值分為泛左值、右值；
泛左值分為左值和將亡值(涉及右值引用)
右值可分為純右值和將亡值(涉及右值引用)

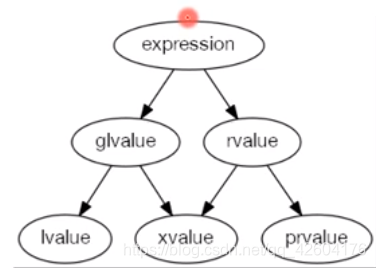
左值指定了一個函數或者對象(表達式計算得出的結果)，它是一個可以取地址的表達式。
也就是說，如果一個函數或者對象可以取地址，那么他就是一個左值。

int lv1{ 42 }; // Object
int main() {int& lv2{ lv1 }; // Lvalue reference to Objectint* lv3{ &lv1 }; // Pointer to Object
}
int& lv4() { return lv1; } // Function returning Lvalue Reference

左值例子:

(1) 解引用表達式p
(2) 字符串字面量"abc"
(3) 前置自增/自減表達式 ++i / --i
(4) 賦值或復合運算符表達式(x=y或m=n等）

純右值是不和對象相關聯的值(字面量)或者其求值結果是字面量或者一個匿名的臨時對象.
純右值例子:

(1) 除字符串字面量以外的字面量，比如 32, ‘a’

(2) 返回非引用類型的函數調用 int f() { return 1;}

(3) 后置自增/自減表達式i++/i–

(4) 算術/邏輯/關系表達式（a+b、a&b、a<<b）（a&&b、a||b、~a）（a==b、a>=b、a<b）

(5) 取地址（&x）

如：

72.0f
a–
x為一個整型變量，&x

左值可以當成右值使用

將亡值

將亡值也指定了一個對象，是一個將純右值轉換為右值引用的表達式:
&&這里不是邏輯與運算符，而是右值引用

int&& rvr1{ 22 }; // 右值引用可以引用純右值

我們先來看什么是左值引用：
a是個左值，b是a的引用，為左值引用。

int a = 1;
int& b = a;

如果a是個常量22，我們對其引用就會出錯：
如下：

int& b{22};		//錯！非常量左值引用不可引用純右值

為了解決這個問題，可以使用const 引用(常量左值引用)引用純右值：
這樣就能保證22(純右值)不會通過b修改，這樣b就相當于是22的別名。

const int& b{22};

當然還有另一種引用純右值的方法就是右值引用了：
通過右值引用可以使純右值的生存期增加，例如：
int&& rvr1{ 22 }; // 右值引用可以引用純右值
int rv2 =++rv1;
原本22在執行完第一個語句就會消亡，但是使用右值引用之后，就可以在后面的語句通過調用右值引用，繼續使用這個值了。

總例：

int prv(int x) { return 6 * x; } // pure rvalue int main() {const int& lvr5{ 21 }; // 常量左值引用可引用純右值int& lvr6{ 22 }; // 錯！非常量左值引用不可引用純右值int&& rvr1{ 22 }; // 右值引用可以引用純右值int& lvr7{ prv(2) }; // 錯！非常量左值引用不可引用純右值int&& rvr2{ prv(2) }; // 右值引用普通函數返回值rvr1 = ++rvr2; // 右值引用做左值使用}