最短公共子序列

Problem statement:

問題陳述：

Given two strings, you have to find the shortest common super sequence between them and print the length of the super sequence.

給定兩個字符串，您必須找到它們之間最短的公共超級序列，并打印超級序列的長度。

    Input:
T Test case
T no of input string will be given to you.
E.g.
3
abcd abxy
sghk rfgh
svd vjhfd
Constrain 
1≤ length (string1) ≤100
1≤ length (string2) ≤100
Output:
Print the length of the shortest super sequence formed from these two strings.

Example

例

    T=3
Input:
abcd abxy
Output:
6 (abcdxy)
Input:
sghk rfgh
Output:
6 (srfghk)
Input:
svd vjhfd
Output:
6 (svjhfd)

Explanation with example:

舉例說明：

Let there are two strings str1 and str2.

假設有兩個字符串str1和str2 。

    str1 = "abcd" 
str2 = "abxy"

To find out the length of the super sequence from these two string is a bit difficult. To solve this problem we have to follow these steps:

從這兩個字符串中找出超級序列的長度有些困難。 要解決此問題，我們必須遵循以下步驟：

1. We have to find out the longest common subsequence between the two strings. From "abcd" and "abxy" the longest common subsequence is "ab".

   我們必須找出兩個字符串之間最長的公共子序列。 從“ abcd”和“ abxy”開始，最長的公共子序列是“ ab”。

2. After getting the longest common subsequence we will add the non-common elements with the longest common subsequence. Non-common characters from "abcd" is "cd" and from "abxy" is "xy".

   得到最長的公共子序列后，我們將添加具有最長的公共子序列的非公共元素。 來自“ abcd”的非常見字符為“ cd”，來自“ abxy”的非常見字符為“ xy”。

3. Therefore the length of the shortest common super sequence is:

   因此，最短公共超序列的長度為：

       length of the two strings-length of the longest common subsequencs
   
   The length of the shortest common super sequence is 

   6 (abcdxy) 6(abcdxy)

Using a dynamic programming algorithm to find out the longest common subsequence between two given string is very efficient and fast as compared to the recursion approach.

與遞歸方法相比，使用動態編程算法找出兩個給定字符串之間最長的公共子序列非常有效且快速。

Let f(a,b) = count the number of common subsequences from the two string starting from 0 to position a and starting from 0 to position b.

令f(a，b) =計算兩個字符串中從0開始到位置a以及從0開始到位置b的公共子序列數。

Considering the two facts:

考慮到兩個事實：

1. If the character of string1 at index a and character of string1 at index b are the same then we have to count how many characters are the same between the two strings before these indexes? Therefore,

   如果索引a的字符串 1的字符和索引b的字符串 1的字符相同，那么我們必須計算在這些索引之前兩個字符串之間有多少個相同的字符？ 因此，

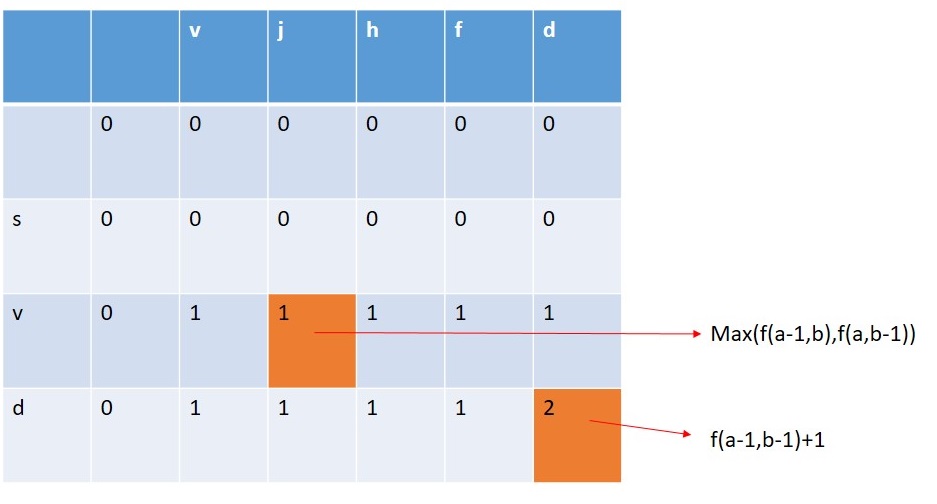
       f(a,b)=f(a-1,b-1)+1
   
   

2. If the character of string1 at index a and character of string1 at index b are not same then we have to calculate the maximum common character count between (0 to a-1 of string1 and 0 to b of string2) and (0 to a of string1 and 0 to b-1 of string2).

   如果字符串 2中的索引和字符串1的字符索引b中的符不相同，則我們來計算之間的最大公共字符計數(0到字符串1的A-1和0至b 字符串2)和(0至a的string1和0到string2的 b-1 )。

       f(a,b)=max?(?(f(a-1,b),f(a,b-1))
   
   

For the two strings:

對于兩個字符串：

    str1 = "abcd"
str2 = "abxy"

Problem solution:

問題方案：

Recursive algorithm:

遞歸算法：

    int Function(str1,pos1,str2,pos2):
if pos1>=str1.length() || pos2>=str2.length()
return 0
for a=pos1 to 0 
for b=pos1 to 0
if str[a]==str[a+l-1]
return Function(str1,a-1,str2,b-1)+1
else
return max(Function(str1,a,str2,b-1),Function(str1,a-1,str2,b));

DP conversion:

DP轉換：

    int Function(str1,str2):
arr[len1+1][len2+1]
for len=1 to str1.length()
for a=1 to str2.length()
if str[a]==str[b]
arr[a][b]=arr[a-1][b-1]+1
else
arr[a][b]=max(arr[a][b-1],arr[a-1][b])
return arr[len1-1][len2-1]

C++ Implementation:

C ++實現：

#include <bits/stdc++.h>
using namespace std;
int count_common_subsequence(string str1, string str2)
{
int len1 = str1.length();
int len2 = str2.length();
int arr[len1 + 1][len2 + 1];
memset(arr, 0, sizeof(arr));
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (str1[i - 1] == str2[j - 1]) {
arr[i][j] = arr[i - 1][j - 1] + 1;
}
else {
arr[i][j] = max(arr[i - 1][j], arr[i][j - 1]);
}
}
}
return arr[len1][len2];
}
int main()
{
int t;
cout << "Test Case : ";
cin >> t;
while (t--) {
string str1, str2;
cout << "Enter the strings : ";
cin >> str1 >> str2;
cout << "Length of the longest common subsequence: " << count_common_subsequence(str1, str2) << endl;
}
return 0;
}

Output

輸出量

Test Case : 3
Enter the strings : svd vjhfd
Length of the longest common subsequence: 2
Enter the strings : sghk rfgh
Length of the longest common subsequence: 2
Enter the strings : abcd abxy
Length of the longest common subsequence: 2

翻譯自: https://www.includehelp.com/icp/shortest-common-super-sequence.aspx

最短公共子序列