原題鏈接：

457. 環形數組是否存在循環

https://leetcode.cn/problems/circular-array-loop/description/

完成情況：

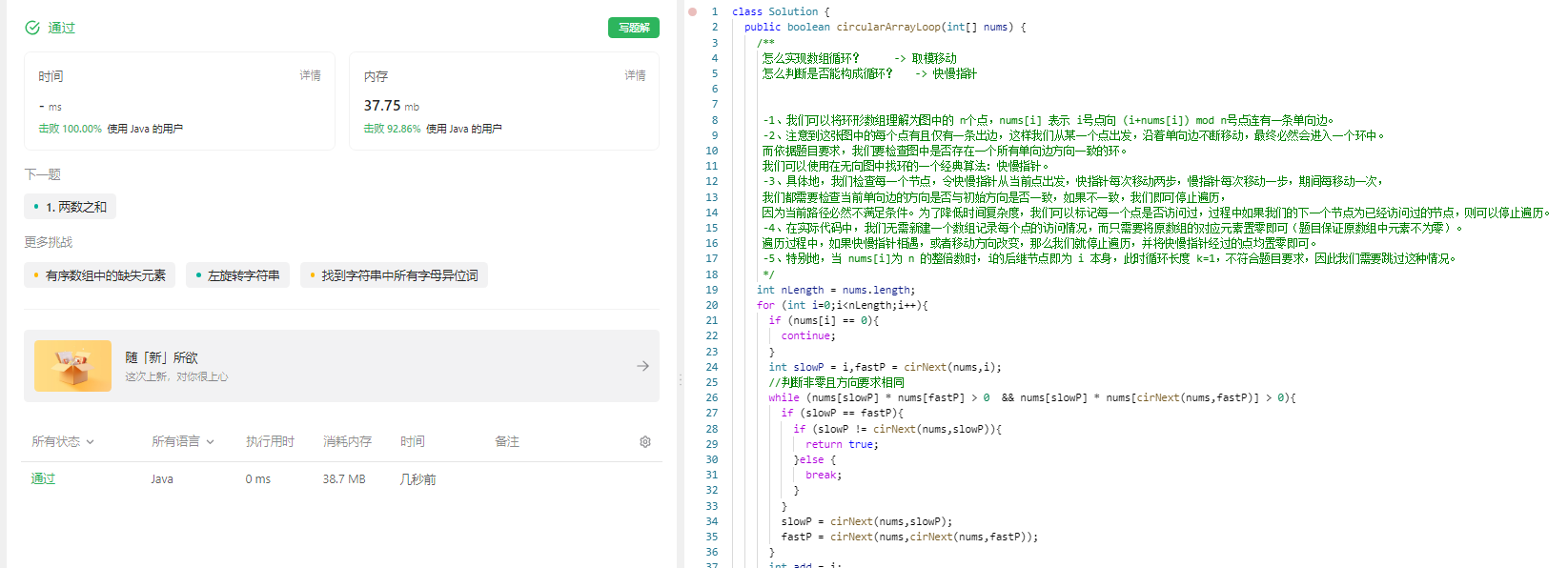
解題思路：

	/**怎么實現數組循環？     -> 取模移動怎么判斷是否能構成循環？   -> 快慢指針-1、我們可以將環形數組理解為圖中的 n個點，nums[i] 表示 i號點向 (i+nums[i]) mod n號點連有一條單向邊。-2、注意到這張圖中的每個點有且僅有一條出邊，這樣我們從某一個點出發，沿著單向邊不斷移動，最終必然會進入一個環中。而依據題目要求，我們要檢查圖中是否存在一個所有單向邊方向一致的環。我們可以使用在無向圖中找環的一個經典算法：快慢指針。-3、具體地，我們檢查每一個節點，令快慢指針從當前點出發，快指針每次移動兩步，慢指針每次移動一步，期間每移動一次，我們都需要檢查當前單向邊的方向是否與初始方向是否一致，如果不一致，我們即可停止遍歷，因為當前路徑必然不滿足條件。為了降低時間復雜度，我們可以標記每一個點是否訪問過，過程中如果我們的下一個節點為已經訪問過的節點，則可以停止遍歷。-4、在實際代碼中，我們無需新建一個數組記錄每個點的訪問情況，而只需要將原數組的對應元素置零即可（題目保證原數組中元素不為零）。遍歷過程中，如果快慢指針相遇，或者移動方向改變，那么我們就停止遍歷，并將快慢指針經過的點均置零即可。-5、特別地，當 nums[i]為 n 的整倍數時，i的后繼節點即為 i 本身，此時循環長度 k=1，不符合題目要求，因此我們需要跳過這種情況。*/

參考代碼：

package 西湖算法題解___中等題;public class __457環形數組是否存在循環 {/*題目翻譯：就是說，有一個數組，可以認為是形成了環的數組里面的元素，【正數】代表向前移動多少個，【負數】代表向后退多少個問？！其中是否存在部分子數組能構成一個循環移動保持不變順序的數組*/public boolean circularArrayLoop(int[] nums) {/**怎么實現數組循環？     -> 取模移動怎么判斷是否能構成循環？   -> 快慢指針-1、我們可以將環形數組理解為圖中的 n個點，nums[i] 表示 i號點向 (i+nums[i]) mod n號點連有一條單向邊。-2、注意到這張圖中的每個點有且僅有一條出邊，這樣我們從某一個點出發，沿著單向邊不斷移動，最終必然會進入一個環中。而依據題目要求，我們要檢查圖中是否存在一個所有單向邊方向一致的環。我們可以使用在無向圖中找環的一個經典算法：快慢指針。-3、具體地，我們檢查每一個節點，令快慢指針從當前點出發，快指針每次移動兩步，慢指針每次移動一步，期間每移動一次，我們都需要檢查當前單向邊的方向是否與初始方向是否一致，如果不一致，我們即可停止遍歷，因為當前路徑必然不滿足條件。為了降低時間復雜度，我們可以標記每一個點是否訪問過，過程中如果我們的下一個節點為已經訪問過的節點，則可以停止遍歷。-4、在實際代碼中，我們無需新建一個數組記錄每個點的訪問情況，而只需要將原數組的對應元素置零即可（題目保證原數組中元素不為零）。遍歷過程中，如果快慢指針相遇，或者移動方向改變，那么我們就停止遍歷，并將快慢指針經過的點均置零即可。-5、特別地，當 nums[i]為 n 的整倍數時，i的后繼節點即為 i 本身，此時循環長度 k=1，不符合題目要求，因此我們需要跳過這種情況。*/int nLength = nums.length;for (int i=0;i<nLength;i++){if (nums[i] == 0){continue;}int slowP = i,fastP = cirNext(nums,i);//判斷非零且方向要求相同while (nums[slowP] * nums[fastP] > 0  && nums[slowP] * nums[cirNext(nums,fastP)] > 0){if (slowP == fastP){if (slowP != cirNext(nums,slowP)){return true;}else {break;}}slowP = cirNext(nums,slowP);fastP = cirNext(nums,cirNext(nums,fastP));}int add = i;while (nums[add] * nums[cirNext(nums,add)] > 0){int temp = add;add = cirNext(nums,add);nums[temp] = 0;}}return false;}/*** 模擬數組循環，即對數值進行取模判斷** @param nums* @param curP* @return*/private int cirNext(int[] nums, int curP) {int nLength = nums.length;return ((curP + nums[curP]) % nLength + nLength)%nLength;}
}

經驗吸取

數組循環判斷 -> 快慢指針