定義
最多有兩棵子樹的有序樹,稱為二叉樹。二叉樹是一種特殊的樹。
遞歸定義:二叉樹是n(n>=0)個有限結點構成的集合。N=0稱為空二叉樹;n>0的二叉樹由一個根結點和兩互不相交的,分別稱為左子樹和右子樹的二叉樹構成。
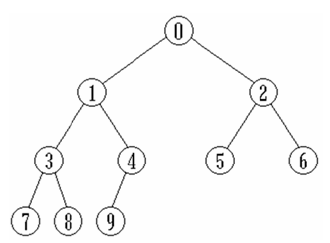
二叉樹中任何結點的第1個子樹稱為其左子樹,左子樹的根稱為該結點的左孩子;二叉樹中任何結點的第2個子樹稱為其右子樹,左子樹的根稱為該結點的右孩子。如下圖是一個二叉樹:
圖1.二叉樹
滿二叉樹和完全二叉樹
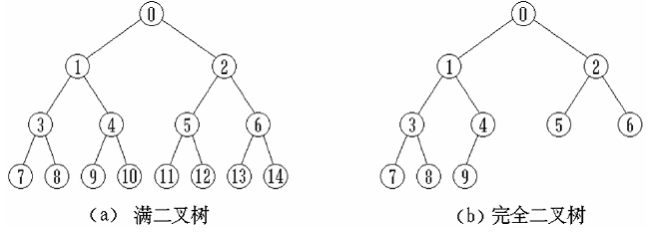
在一棵二叉樹中,如果所有分支結點都存在左子樹和右子樹,并且葉子結點都在同一層上,這樣的二叉樹稱作滿二叉樹。一棵深度為k且由2k-1個結點的二叉樹稱為滿二叉樹。
如果一棵具有n個結點的二叉樹的結構與滿二叉樹的前n個結點的結構相同,這樣的二叉樹稱作完全二叉樹。
圖2. 滿二叉樹和完全二叉樹
基本性質
這里規定二叉樹的根結點的層次為1。
性質1:則二叉樹的第i 層最多有2i-1個結點(在此二叉樹的層次從1開始,i≥1)
性質2:深度為k的二叉樹最多有2k-1個結點。(k≥1)
性質3:對任何一棵二叉樹T, 如果其葉結點個數為n0, 度為2的非葉結點個數為n2, 則有
??????? ?????n0 = n2?+ 1
性質4:具有 n(n>0)個結點的完全二叉樹的深度為?log2n?+1;?x?表示不超過x的最大整數。
性質5:如果對一棵有n個結點的完全二叉樹的結點按層序編號(從第1層到第?l og2n? +1層,每層從左到右),則對任一結點i(1≤i≤n),有:
(1)如果i=1,則結點i無雙親,是二叉樹的根;如果i>1,則其雙親是結點?i/2?。
(2) 如果2i<=n, 則結點i的左孩子結點是2i;否則,結點i為葉子結點,無左孩子結點。
(3)如果2i+1<=n,則結點i的右孩子是結點2i+1; 否則,結點i為葉子結點,無右孩子結點。
抽象數據類型
數據元素:具有相同特性的數據元素的集合。
結構關系:樹中數據元素間的結構關系由二叉樹的定義確定。
基本操作:樹的主要操作有
(1)創建樹IntTree(&T)
(2)銷毀樹DestroyTree(&T)
(3)構造樹CreatTree(&T,deinition)
(4)置空樹ClearTree(&T)
(5)判空樹TreeEmpty(T)
(6)求樹的深度TreeDepth(T)
(7)獲得樹根Root(T)
(8)獲取結點Value(T,cur_e,&e),將樹中結點cur_e存入e單元中。
(9)數據賦值Assign(T,cur_e,value),將結點value,賦值于樹T的結點cur_e中。
(10)獲得雙親Parent(T,cur_e),返回樹T中結點cur_e的雙親結點。
(11)獲得最左孩子LeftChild(T,cur_e),返回樹T中結點cur_e的最左孩子。
(12)獲得右兄弟RightSibling(T,cur_e),返回樹T中結點cur_e的右兄弟。
(13)插入子樹InsertChild(&T,&p,i,c),將樹c插入到樹T中p指向結點的第i個子樹之前。
(14)刪除子樹DeleteChild(&T,&p,i),刪除樹T中p指向結點的第i個子樹。
(15)遍歷樹TraverseTree(T,visit())
二叉樹的存儲結構
?二叉樹是非線性結構,即每個數據結點至多只有一個前驅,但可以有多個后繼。它可采用順序存儲結構和鏈式存儲結構。
1.順序存儲結構
????二叉樹的順序存儲,就是用一組連續的存儲單元存放二叉樹中的結點。因此,必須把二叉樹的所有結點安排成為一個恰當的序列,結點在這個序列中的相互位置能反映出結點之間的邏輯關系,用編號的方法從樹根起,自上層至下層,每層自左至右地給所有結點編號,缺點是有可能對存儲空間造成極大的浪費,在最壞的情況下,一個深度為k且只有k個結點的右單支樹需要2k-1個結點存儲空間。依據二叉樹的性質,完全二叉樹和滿二叉樹采用順序存儲比較合適,樹中結點的序號可以唯一地反映出結點之間的邏輯關系,這樣既能夠最大可能地節省存儲空間,又可以利用數組元素的下標值確定結點在二叉樹中的位置,以及結點之間的關系。圖5-5(a)是一棵完全二叉樹,圖5-5(b)給出的圖5-5(a)所示的完全二叉樹的順序存儲結構。

?(a)??一棵完全二叉樹??????????????????(b)????順序存儲結構
圖5-5?完全二叉樹的順序存儲示意圖
????對于一般的二叉樹,如果仍按從上至下和從左到右的順序將樹中的結點順序存儲在一維數組中,則數組元素下標之間的關系不能夠反映二叉樹中結點之間的邏輯關系,只有增添一些并不存在的空結點,使之成為一棵完全二叉樹的形式,然后再用一維數組順序存儲。如圖5-6給出了一棵一般二叉樹改造后的完全二叉樹形態和其順序存儲狀態示意圖。顯然,這種存儲對于需增加許多空結點才能將一棵二叉樹改造成為一棵完全二叉樹的存儲時,會造成空間的大量浪費,不宜用順序存儲結構。最壞的情況是右單支樹,如圖5-7?所示,一棵深度為k的右單支樹,只有k個結點,卻需分配2^k-1個存儲單元。

(a)?一棵二叉樹??????????????????????????(b)?改造后的完全二叉樹

(c)?改造后完全二叉樹順序存儲狀態
圖5-6?一般二叉樹及其順序存儲示意圖

?(a)?一棵右單支二叉樹??????(b)?改造后的右單支樹對應的完全二叉樹

? ? (c)?單支樹改造后完全二叉樹的順序存儲狀態
???????????????????圖5-7?右單支二叉樹及其順序存儲示意圖
????結構5-1二叉樹的順序存儲
#define Maxsize 100 //假設一維數組最多存放100個元素
typedef char Datatype; //假設二叉樹元素的數據類型為字符
typedef struct
{ Datatype bt[Maxsize];int btnum;}Btseq; 2.鏈式存儲結構
????二叉樹的鏈式存儲結構是指,用鏈表來表示一棵二叉樹,即用鏈來指示元素的邏輯關系。
通常的方法是鏈表中每個結點由三個域組成,數據域和左右指針域,左右指針分別用來給出該結點左孩子和右孩子所在的鏈結點的存儲地址。其結點結構為:

? 其中,data域存放某結點的數據信息;lchild與rchild分別存放指向左孩子和右孩子的指針,當左孩子或右孩子不存在時,相應指針域值為空(用符號∧或NULL表示)。利用這樣的結點結構表示的二叉樹的鏈式存儲結構被稱為二叉鏈表,如圖5-8所示。 ?

(a)?一棵二叉樹???????????????????????????(b)?二叉鏈表存儲結構
??????????????????圖5-8???二叉樹的二叉鏈表表示示意圖
????為了方便訪問某結點的雙親,還可以給鏈表結點增加一個雙親字段parent,用來指向其雙親結點。每個結點由四個域組成,其結點結構為:

?這種存儲結構既便于查找孩子結點,又便于查找雙親結點;但是,相對于二叉鏈表存儲結構而言,它增加了空間開銷。利用這樣的結點結構表示的二叉樹的鏈式存儲結構被稱為三叉鏈表。
????圖5-9給出了圖5-8?(a)所示的一棵二叉樹的三叉鏈表表示。

?圖5-9二叉樹的三叉鏈表表示示意圖
????盡管在二叉鏈表中無法由結點直接找到其雙親,但由于二叉鏈表結構靈活,操作方便,對于一般情況的二叉樹,甚至比順序存儲結構還節省空間。因此,二叉鏈表是最常用的二叉樹存儲方式。
結構5-2二叉樹的鏈式存儲
#define datatype char //定義二叉樹元素的數據類型為字符
typedef struct node //定義結點由數據域,左右指針組成
{ Datatype data;struct node *lchild,*rchild;}Bitree;

)




)
)






)
)




)