matlab拼碎紙片過程,碎紙片拼接復原模型

1. 引言

破碎文件的拼接在司法物證復原、歷史文獻修復以及軍事情報獲取等領域都有著重要的應用。企事業、機關、院校和軍隊基于保密的需要，使用碎紙機對重

要文件，單據以及材料進行銷毀。一些重要的文件隨著時間流逝，殘破不全，因此，又需要將已經破碎的文檔重新恢復。

傳統上，拼接復原工作需由人工完成，準確率較高，但效率很低。特別是當碎片數量巨大，人工拼接很難在短時間內完成任務。隨著當代科技和計算機技術的快速發展，人們試圖開發碎紙片自動拼接技術，以提高對碎紙片文件和圖片的拼接復原效率。

國內一些學者對碎紙片復原技術進行了研究，其中周豐提出了一種基于序列的二維圖像碎紙片輪廓匹配算法[1]，何鵬飛研究了基于蟻群優化算法的紙片拼接技術[2]，羅智中[3]研究了基于文字特征的文檔碎紙片半自動拼接方法，除此之外學者們還提出并研究了其他各種相應的技術[4-10]。然而目前通過計算機算法對破碎文檔進行恢復的技術研究還不多，基本上沒有一種全自動的碎紙片恢復技術，因此，一種能夠快速且高效的恢復碎紙機數據文檔技術的研究有巨大的現實意義。本文在借鑒其他學者研究基礎上，對邊緣規范的碎紙片拼接技術進行了研究。

2. 模型假設及符號說明

2.1. 模型假設

1) 設碎紙圖片與真實文件紙張大小、顏色、邊緣情況相同；

2) 假設碎紙照片邊緣完整，不存在破損；

3) 假設所有碎紙片的掃描情況相同；

2.2. 符號說明

i ——編號i的圖片的灰度矩陣；

i ——編號i的圖片二值化處理后矩陣；

i ——編號i的圖片二維邊緣矩陣；

′

″

? ——邊緣匹配度矩陣；

i ——編號

i 的圖片再次處理后的0-1矩陣；

F ——邊緣匹配度之和矩陣。

3. 問題分析

3.1. 中文碎紙片的分析

本論文數據來源于2013年全國大學生數學建模試題B題附件3、4，碎紙片均為一份紙張撕裂所得，不會存在含有相同信息的公共部分，下面不再重述。

附件3、4中所給的圖片為掃描原紙張碎片后得到的BMP格式的圖片，圖片像素均為

180

72 ，使用matlab中的imread函數[11,12]可做出圖片的灰度矩陣

i (

209 )。舉例如下(由于該像素圖片轉換后為

180

72 的矩陣，論文中無法放置，所以僅簡單舉例說明，論文中若還出現龐大的矩陣，同本說明)：

(

255

220

150

255

)

矩陣的中元素表示該位置圖片灰度，255表示為白，0為黑，圖片中信息為黑白文字信息，但由于文字信息會存在陰影，所以矩陣中出現了介于0-255的元素。為了方便應用，可對黑白圖片做[13]二值化處理，將上例中

i 轉化為如下0-1矩陣：

(

)

其中白色用0值表示，非白色用1表示。

將附件3、4中

19 張圖片做如上處理得0-1矩陣

(

209

) ，矩陣階數為

180

72 。

分別提取

i 矩陣第1列和第72構成新的

180

2 階邊緣矩陣。搜索所有圖片矩陣發現

128 矩陣中均有一列為0，可認為編號為014和128的圖片為相鄰的兩張圖片，兩張圖片匹配的原則示例如圖1。

將左邊矩陣的第二列元素與右邊矩陣的第一列元素進行兩兩匹配，記錄元素相同的個數，個數除以180為左邊矩陣第二列對右邊矩陣第一列的邊緣匹配度，記為：

元

素

相

同

的

數

量

180

定義：

匹

配

�

180 ——矩陣匹配度

將所有碎紙片的0-1矩陣做如上匹配過程，可依次選取與其匹配的碎紙片。圖1中左邊矩陣第一列與右邊矩陣第二列匹配的原則同上。

將附件3和附件4中各自的209碎紙片做同樣的圖像處理轉化為灰度矩陣后進行二值化處理得到與其相對應的矩陣，根據結果可知圖片轉化后的矩陣為

180

72 階的，若使用邊緣匹配的方法，一張碎紙片對應其他208張碎紙片的邊緣匹配相同的像素點有208種情況，變化范圍為

180 可知若直接采用邊緣匹配中的方法得到的結果可能出現多個相同或無法判斷的情況，所以這里我們先考慮附件中碎紙片的特

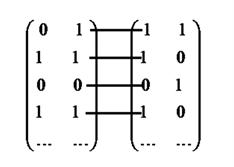
Figure 1. The matching diagram of 014 and 128 two images

圖1. 014與128兩張圖片的匹配示意圖

性。

觀察圖2發現，通過查閱資料分析[3]基于文字特征的文檔碎紙片半自動拼接，每一行的絕大多數中文文字均可認為擁有同一上界、同一下界(圖2最右端出現了“一”字，但是同行還存在其他文字，可認為同一行文字有同一上界與同一下界)，我們可以根據這一特性，利用聚類分析[14]方法并使用Matlab軟件將匹配度高及位置相同的碎紙片歸類為一組[3]。

利用聚類方法歸類步驟：

1) 搜索每一張碎紙片轉化后二值化矩陣

i 的每一行，若矩陣該行中存在數值1，則將該行全部賦值為1，若這一行元素全為0，則將該行全部賦值為0，其中1表示本行存在灰度小于255的像素，0表示不存在灰度小于255的像素，這樣將209張碎紙片做出新的二值化矩陣

i ；

2) 同3.1的分析取邊緣做邊緣匹配得修改后的邊緣匹配度矩陣

D ，匹配度高則說明碎紙片的文字信息處于同一水平位置，見圖2；

3) 在2)完成后如果未完全匹配，則進行再人工干預，得到較優的結果[11]見圖3。

4) 得到很多組有相同位置的碎紙片后，在每一組內采用邊緣匹配方法，這里為了防止出現兩白邊匹配造成碎紙片連接混亂的現象，要加以限制。方法為：若在組內做邊緣匹配出現匹配度為1的情況，則暫時不連接此碎紙片，從剩余的碎紙片出發做邊緣匹配與其他碎紙片連接，直到組內所有碎紙片均已覆蓋。

5) 這樣再通過一定人工干預可以得到拼接復原后的11橫行碎紙片，再同樣使用邊緣匹配方法，將得到的11行碎紙條長邊進行邊緣匹配做出

11 的匹配度矩陣后找最大匹配度作為連接的碎紙條[15]，同樣為了防止出現兩白邊匹配造成碎紙片連接混亂的現象，要加以限制。方法為：若在組內做邊緣匹配出

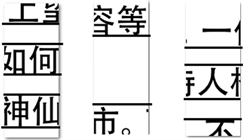
Figure 2. The images after secondary handling

圖2. 處理后的圖片

Figure 3. The images after secondary handling

圖3. 二次處理后的圖片

現匹配度為1的情況，則暫時不連接此碎紙片，從剩余的碎紙片出發做邊緣匹配與其他碎紙片連接，直到11張拼接后的碎紙片均已覆蓋。最后加以人工處理，得到完整的原文件。

3.2. 英文碎紙片的分析

碎紙片的英文在位置上也有一定的規則可循。如圖4。

可以發現英文字母的主要的部分擁有同一上界和同一下界，但是跟中文不同，英文中會出現一些“y”、“d”之類的字母，為了同樣使用3.1中的方法我們通過觀察附件4中圖片的像素情況，將圖片中每一行中黑色像素數少于13(該值的選取是為了方便二值化轉化，也可以選取別的數字)的及字母的次要部分轉變為二值化矩陣中的0，將每一行中黑色像素大于等于13的及字母的主要部分轉化為二值化矩陣中的1，這樣得到的新的二值化矩陣

i ，可認為圖像轉變為下圖5表示的方式，同樣使用3.1中的分析方法將新的二值化矩陣做邊緣匹配，匹配度高的可認為兩碎紙片在原紙張中位于同一行，把匹配度高于0.9的元素分為一組后，對每一組進行邊緣匹配。

考慮英文字符的情況，在3.1基礎上，對組內圖片原始二值化矩陣邊緣匹配度矩陣

D 每一行的搜索，若矩陣的任意一行中出現匹配度大于0.9的元素個數超過2個，則加以人工干預，根據文章的格式、內容選擇應該連接的碎紙片，其他過程同3.1，區別僅為本文中需要對軟件執行過程進行人工干預。

Figure 4. Demonstrates picture 1

圖4. 演示圖片1

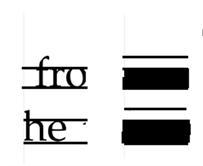
Figure 5. Demonstrates picture 2

圖5. 演示圖片2

4. 模型的建立與求解

4.1. 中文碎紙片復原的模型建立與求解

搜索每一張碎紙片轉化后的0-1矩陣

i 的每一行，若存在黑色即矩陣該行中存在數值1，則將該行全部賦值為1，若這一行不存在黑即此行元素全為0，則將該行全部賦值為0，這樣將209張碎紙片做出新的二值化矩陣

i ，之后按照3.1中的定義做邊緣匹配，做出矩陣大小為

209

209 邊緣匹配度矩陣

D (由于矩陣太大，在論文中不給出)，元素

j 為處理后的碎紙片邊緣二值化矩陣

i 的第二列與處理后的碎紙片邊緣二值化矩陣

j 第一列的邊緣匹配度，匹配度高則說明碎紙片的文字信息處于同一水平位置。在矩陣

D 中每一行選取匹配度大于0.9的元素，進行統計分組，可得結果如表1。

可以看出在取匹配度為0.9及以上時，分出了20個組，其中組內元素最多的為19，組內元素最少的為1。而最后的結果應該為11行，我們需要對這些組中的元素進行合并后得到11行，所以我們要先考慮元素數量為19的組，再考慮其他元素數多的組，對組內圖片進行3.1中的邊緣匹配，匹配后的結果在與元素數少的組做匹配與人工處理。

以第2組為例，該組包含19個元素，對于組內的19個元素的原始二值化矩陣進行上述中的邊緣匹

Table 1. Grouping

表1. 分組情況

配，通過結果觀察本題模型第一步確定模型的可行性，其他的組的處理情況相同，不再重述。結果如表2。

分別復原得到圖片，觀察圖6、圖7。

對于第二問中文碎紙片的復原問題，通過上面的結果發現匹配結果較好，對于中文的碎紙片的拼接復原即使過程中未加入人工干預也可以得到較優的結果。

可發現該組中文字位置符合想象，及同一行中的文字擁有同一上界和同一下界，在這一組中Matlab軟件很好的將碎紙片拼接出來，思考為什么會出現上面圖6、圖7兩者不能匹配在一起的原因。可發現拼

Table 2. Internal group

表2. 內部分組

Figure 6. The second set of splice results (1)

圖6. 第二組拼接結果(1)

Figure 7. The second set of splice results (2)

圖7. 第二組拼接結果(2)

接復原后的圖6、圖7左右兩側均存在白邊，僅用計算機無法識別兩者先后，需加以人工干預，通過對文章的內容、結構、形式的觀察人工拼接，得出結果。改進后的圖片排序見表2，復原圖片見圖8。

通過結果可以發現拼接程度較好，所以也驗證了本問題中碎紙片拼接復原模型可行性。

其他組做相同處理，這樣可得到拼接好的11橫行的碎紙條，對11橫行的碎紙條的長邊進行邊緣匹配，建立新的邊緣匹配矩陣，結果如表3。

以上做出的表格把一些橫行碎紙片拼接在一起，未能拼接的原因是由于拼接后的橫行碎紙片兩端都存在白邊，計算機無法做出順序的判斷，所以我們要根據文字內容、規格、形式等因素人工將它們結合起來，人機結合后的原文件以表4。

觀察發現拼接復原后結果較好。

4.2. 英文碎紙片復原的模型建立與求解

搜索每一張碎紙片轉化后的0-1矩陣Ci的每一行，若存在黑色像素數量大于等于13即矩陣該行中數值1的數量大于等于13，則將該行全部賦值為1，若這一行黑色像素數量小于13，則將該行全部賦值為0，這樣將209張碎紙片做出新的二值化矩陣Ei，之后同4.1的求解過程做邊緣匹配，做出矩陣大小為

209

209 邊緣匹配度矩陣D(由于矩陣太大，在論文中不做出)，

Figure 8. The second set of results after splicing human intervention

圖8. 人工干預后第二組拼接結果

元素

j 為處理后的碎紙片邊緣二值化矩陣i的第二列與處理后的碎紙片邊緣二值化矩陣j第一列的邊緣匹配度，匹配度高則說明碎紙片的文字信息處于同一水平位置。同樣在矩陣D中每一行選取匹配度大于0.9的元素，進行統計分組。

在這里需要強調的是，若分完組后的組內元素進行4.1中的邊緣匹配進行殘片復原，小組成員發現結果十分的不理想，任舉一例，見圖9。

根據圖9可以發現對于本文中的英文殘紙片的文字信息主要內容處于相同水平位置，文字信息處于同一水平位置，結合4.1可以認為首先判斷文字信息未知的方法是正確的。但是組內英文碎紙片的拼接復原程度結果差，圖中部分碎紙片得到了復原，而大部分卻進行了錯誤的拼接。對比4.1的中文復原結果，可以認為英文相對中文會有一定的特殊性。

分析產生問題的原因，由于碎紙片的連接是按照組內圖片兩兩邊緣匹配的大小來決定的，發生如圖的情況說明：實際的對應的碎紙片的邊緣匹配度一般在0.9以上，英文碎紙片實際對應的碎紙片的邊緣匹配度會出現比其他碎紙片的邊緣匹配對小的情況。面對這種問題，我們需要對檢測邊緣匹配度的程序的過程進行人工干預，方法為：其他圖片對當前圖片的邊緣匹配度若出現兩個及兩個以上大于0.9的匹配度，則進行人工干預，根據文章的內容、格式等進行人工拼接復原，其他步驟同4.1。對于本文中對于英文碎紙片的拼接復原問題可用圖10的流程圖表示。

通過上述步驟可一把相同行的紙片先拼接好，得到新的11張橫行碎紙片，這里拼接11張碎紙片的方法同4.1，不再重述，得到的結果見表5。

4.3. 實現算法

索貝爾算子(Sobel operator)是圖像處理中的算子之一，主要用作邊緣檢測。在技術上，它是一離散性差分算子，用來運算圖像亮度函數的梯度之近似值。在圖像的任何一點使用此算子，將會產生對應的梯度矢量或是其法矢量。

Table 3. Long-edge stitching result of shredded paper

表3. 碎紙條的長邊拼接結果

Table 4. The recovery results of Annex 3

表4. 附件3的復原結果

Figure 9. Part of the mosaic picture of the results of the English group after completion

圖9. 英文圖片分完組后的部分拼接結果

該算子包含兩組3 × 3的矩陣，分別為橫向及縱向，將之與圖像作平面卷積，即可分別得出橫向及縱

向的亮度差分近似值。如果以A代表原始圖像，Gx及Gy分別代表經橫向及縱向邊緣檢測的圖像，其公式如下：

(

)

(

)

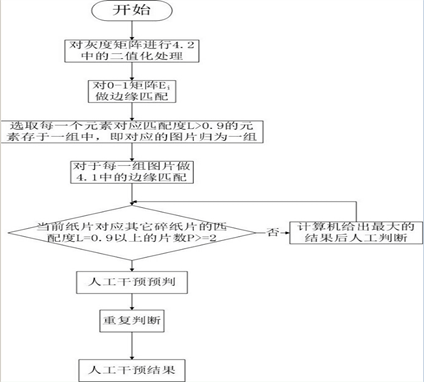
Figure 10. The flow chart

圖10. 流程圖

Table 5. The recovery results of Annex 4

表5. 附件4的復原結果

圖像的每一個像素的橫向及縱向梯度近似值可用以下的公式結合，來計算梯度的大小。

然后可用以下公式計算梯度方向

arctan

(

)

在以上例子中，如果以上的角度Θ等于零，即代表圖像該處擁有縱向邊緣，左方較右方暗。在邊沿檢測中，常用的一種模板是Sobel算子。Sobel算子有兩個，一個是檢測水平邊沿的；另一個是檢測垂直平邊

沿的。Sobel算子對于象素的位置的影響做了加權，因此效果更好。Sobel算子另一種形式是各向同性Sobel(Isotropic Sobel)算子，也有兩個，一個是檢測水平邊沿的，另一個是檢測垂直平邊沿的。各向同性Sobel算子和普通Sobel算子相比，它的位置加權系數更為準確，在檢測不同方向的邊沿時梯度的幅度一致。

4.4. 聚類精度和算法時間復雜度分析

1) 聚類精度分析

傳統的k-means算法，所求的解往往是局部最優解，使用k-means算法在一定程度上減少了局部最優可能性，但從聚類過程看，求的解也往往是局部最優解，本文提出的調整簇閥值的加速算法，由于采用了近似的k-means算法，導致該算法只能找到局部近似解。適當地設置閥值，也能得到和k-means算法相當的聚類精度。

2) 時間復雜度分析

傳統k-means算法的時間復雜度為

(

) ，其中，n為樣本個數，k為簇數目，d為數據維數，t為迭代次數。

5. 模型的評價與推廣

5.1. 模型的優點

通過對復原后圖片驗證結果認為碎紙片復原拼接模型對于本問題有很高的可行性。對于中、英文兩種情況，發現了中文需要人工干預較少，英文人工干預較多的規律，說明不同語言有各自的特性，中文到英文由于難度的增加依次將模型進行改進，給出了嚴謹的說明過程，模型對該類問題有很好的可用性。

5.2. 模型的缺點

本模型僅適合規則碎紙片黑白信息的復原問題，不能解決不規則碎紙片的復原與非黑白信息的復原。人工干預占總過程時間的比例相對較高(35%)，對于數據量大的碎紙片復原問題，人工干預可能會花掉大部分時間。

5.3. 模型的推廣

該模型適用于規則碎紙片的拼接復原問題。本模型給出了中英文碎片處理的算法，根據復原結果，可認為本論文中的模型很好的適用于該類問題的解決。對于一些不熟悉的語言和符號信息，碎紙片的倒置情況未知，需要先對倒置情況進行判斷，再進行類似的算法進行圖片復原處理問題。

對于規則殘片，如考古挖出的規則的文物、規則的鈔票殘片等殘片復原問題，只需將它們用照片照好轉化為灰度矩陣，對顏色進行一定的處理后借鑒本模型方法進行復原。