2.4_數理統計的基本概念

數理統計思維導圖

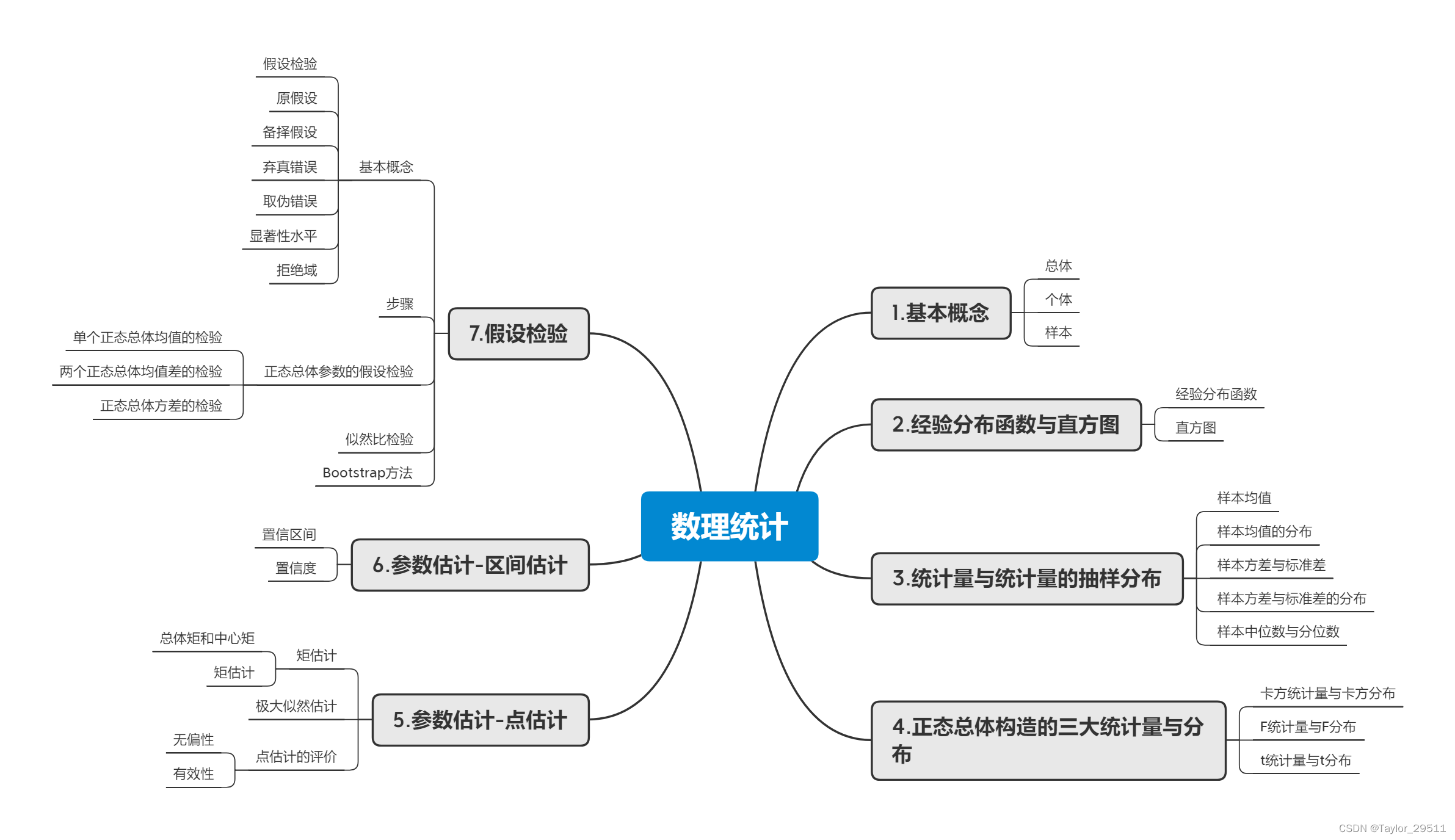
更多詳細內容見notebook

1.基本概念

總體：研究對象的全體，它是一個隨機變量，用$X$表示。

個體：組成總體的每個基本元素。

簡單隨機樣本：來自總體$X$的$n$個相互獨立且與總體同分布的隨機變量$X_1,X_2?,X_n$，稱為容量為$n$的簡單隨機樣本，簡稱樣本。

統計量：設$X_1,X_2?,X_n,$是來自總體$X$的一個樣本，$g(X_1,X_2?,X_n)$）是樣本的連續函數，且$g()$中不含任何未知參數，則稱$g(X_1,X_2?,X_n)$為統計量。

樣本均值：
$\overline{X}=\frac{1}{n}{\sum }_{i=1}^n{X}_i$
樣本方差：$S^2=\frac{1}{n?1}{\sum }_{i=1}^n{(X_i?\overline{X})}^2$

樣本矩：樣本$k$階原點矩：$A_k=\frac{1}{n}{\sum }_{i=1}^n{X}_i^k,k=1,2,?$

樣本$k$階中心矩：$B_k=\frac{1}{n}{\sum }_{i=1}^n{(X_i?\overline{X})}^k,k=1,2,?$

2.分布

${\chi }^2$分布：${\chi }^2=X_1^2+X_2^2+?+X_n^2～{\chi }^2(n)$，其中$X_1,X_2?,X_n,$相互獨立，且同服從$N(0,1)$

$t$分布：$T=\frac{X}{\sqrt{Y/n}}～t(n)$ ，其中$X～N\left(0,1\right),Y～{\chi }^2(n),$且$X$，$Y$ 相互獨立。

$F$分布：$F=\frac{X/n_1}{Y/n_2}～F(n_1,n_2)$，其中$X～{\chi }^2\left(n_1\right),Y～{\chi }^2(n_2),$且$X$，$Y$相互獨立。

分位數：若$P(X\le x_{\alpha })=\alpha ,$則稱$x_{\alpha }$為$X$的$\alpha$分位數

3.正態總體的常用樣本分布

設$X_1,X_2?,X_n$為來自正態總體$N(\mu ,{\sigma }^2)$的樣本，$\overline{X}=\frac{1}{n}{\sum }_{i=1}^n{X}_i,S^2=\frac{1}{n?1}{\sum }_{i=1}^n{(X_i?\overline{X})}^2,$則：

(1) $\overline{X}～N\left(\mu ,\frac{{\sigma }^2}{n}\right)$或者$\frac{\overline{X}?\mu }{\frac{\sigma }{\sqrt{n}}}～N(0,1)$

(2) $\frac{(n?1)S^2}{{\sigma }^2}=\frac{1}{{\sigma }^2}{\sum }_{i=1}^n{(X_i?\overline{X})}^2～{\chi }^2(n?1)$

(3) $\frac{1}{{\sigma }^2}{\sum }_{i=1}^n{(X_i?\mu )}^2～{\chi }^2(n)$

(4) $\frac{\overline{X}?\mu }{S/\sqrt{n}}～t(n?1)$

4.重要公式與結論

(1) 對于${\chi }^2～{\chi }^2(n)$，有$E({\chi }^2(n))=n,D({\chi }^2(n))=2n;$

(2) 對于$T～t(n)$，有$E(T)=0,D(T)=\frac{n}{n?2}(n>2)$；

(3) 對于$F\stackrel{~}{}F(m,n)$，有 $\frac{1}{F}～F(n,m),F_{a/2}(m,n)=\frac{1}{F_{1?a/2}(n,m)};$

(4) 對于任意總體$X$，有 $E(\overline{X})=E(X),E(S^2)=D(X),D(\overline{X})=\frac{D(X)}{n}$