題目

難度：簡單

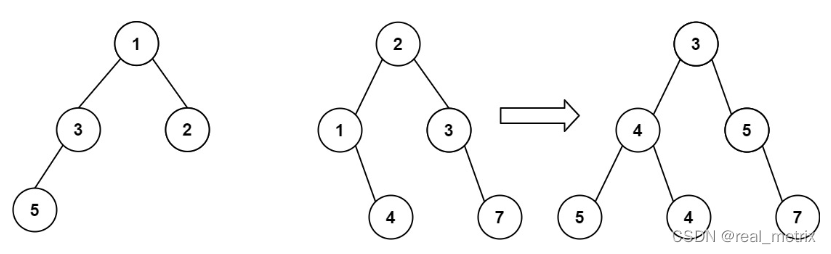
給你兩棵二叉樹： root1 和 root2 。

想象一下，當你將其中一棵覆蓋到另一棵之上時，兩棵樹上的一些節點將會重疊（而另一些不會）。你需要將這兩棵樹合并成一棵新二叉樹。合并的規則是：如果兩個節點重疊，那么將這兩個節點的值相加作為合并后節點的新值；否則，不為 null 的節點將直接作為新二叉樹的節點。

返回合并后的二叉樹。

注意: 合并過程必須從兩個樹的根節點開始。

思路

1. 本題可以通過常見的二叉樹的遍歷方式（同時也是遞歸的方式），同時遍歷兩棵樹，每次遍歷獲取相同的節點，然后根據以下三種情況求和
   1. 若遍歷到的位置均不為空，則對兩個節點求和，將求和的結果覆蓋 root2 的這個節點
   2. 若遍歷到的位置，root1 為空，則返回 root2 的值（root2 為空也返回）
   3. 若遍歷到的位置，root2 為空，則返回 root1 的值（root1 為空也返回）
2. 對代碼的圖解見代碼實現部分

代碼實現

本代碼采用前序遍歷的方式來遍歷兩棵二叉樹

    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if (root1 == nullptr) {return root2;}if (root2 == nullptr) {return root1;}root2->val = root2->val + root1->val;root2->left = mergeTrees(root1->left, root2->left);root2->right = mergeTrees(root1->right, root2->right);return root2;}

下面通過一個示意圖來演示遞歸的效果（左樹為 root1，右樹為 root2，右側方框表示函數棧）

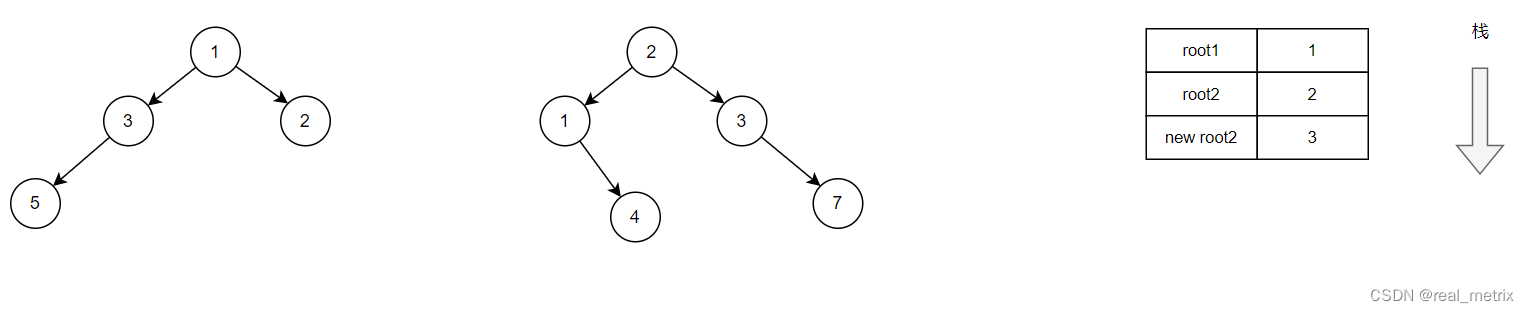
首先，root1 和 root2 入棧，此時它們分別指向的值是 1,2，按照求和的要求，符合情況 1，于是 root2 的值更新為 3。

此時代碼執行到了 root2->left = mergeTrees(root1->left, root2->left); 處，我們繼續將 root1，root2 的左節點傳入遞歸函數。

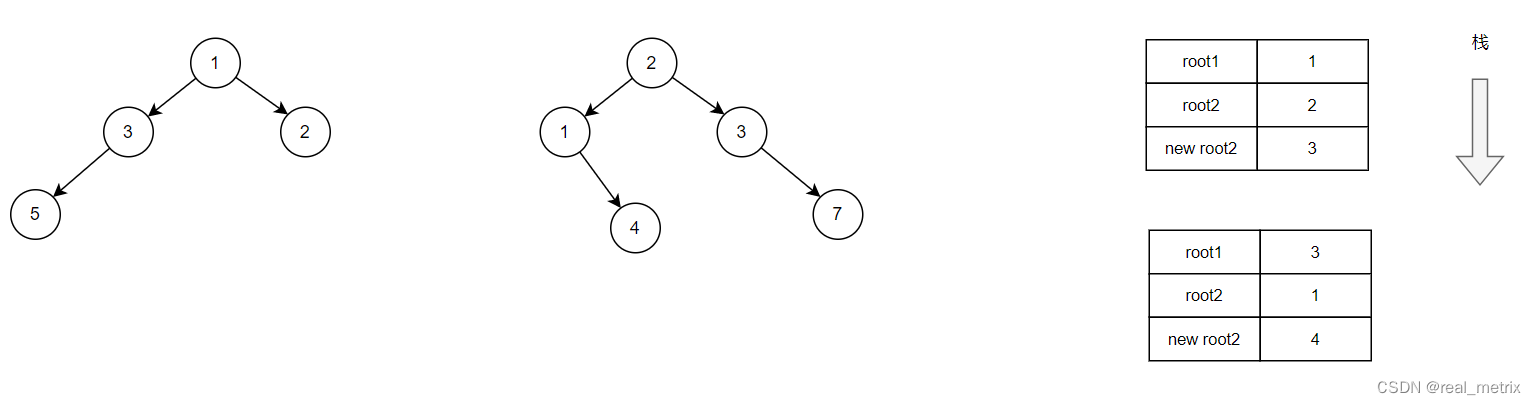
如圖，我們看到出現了一個新的函數調用棧，此時的 root1 和 root2 為 3 和 1，它們分別是傳入的上一層函數中的 root1->left 和 root2->left 的值。

同理計算 root2->val = root2->val + root1->val; 得到 root2 的值為 4。

此時代碼執行到了 root2->left = mergeTrees(root1->left, root2->left); 處，我們繼續將 root1，root2 的左節點傳入遞歸函數。

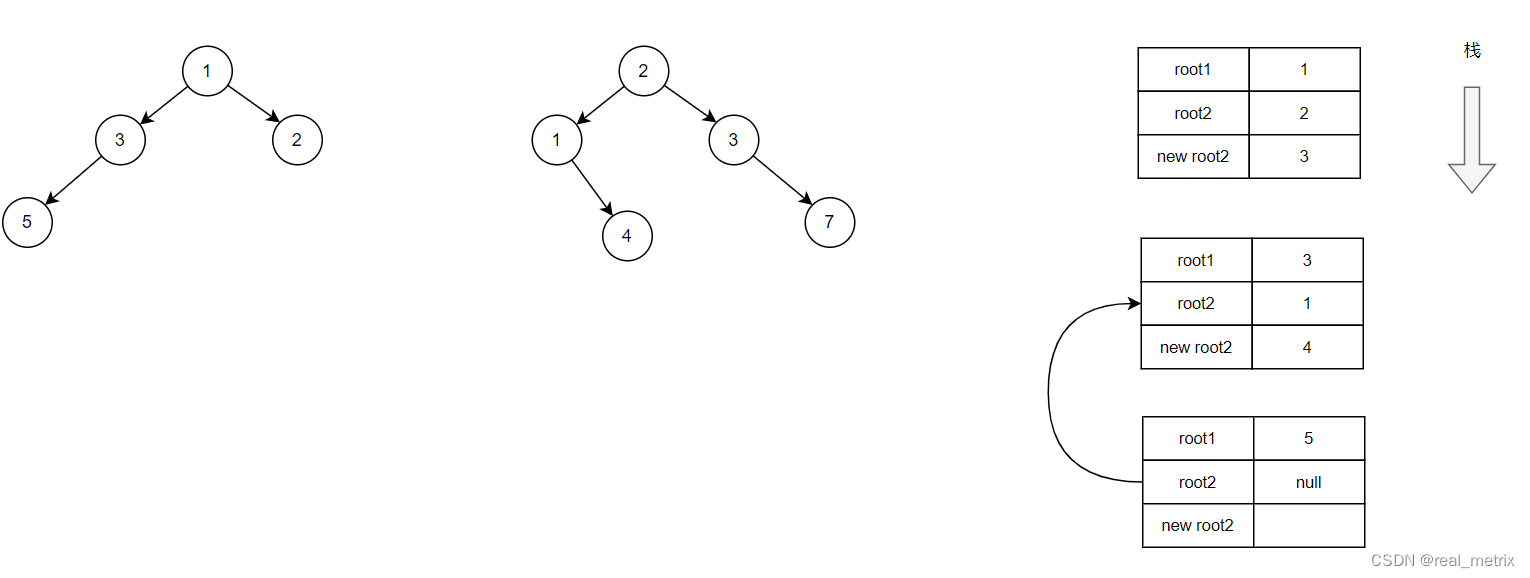
在該層遞歸的代碼中，因為 root2 為 null，所以觸發了以下這段代碼，于是此棧被銷毀，并返回上一層棧中。

        if (root2 == nullptr) {return root1;}

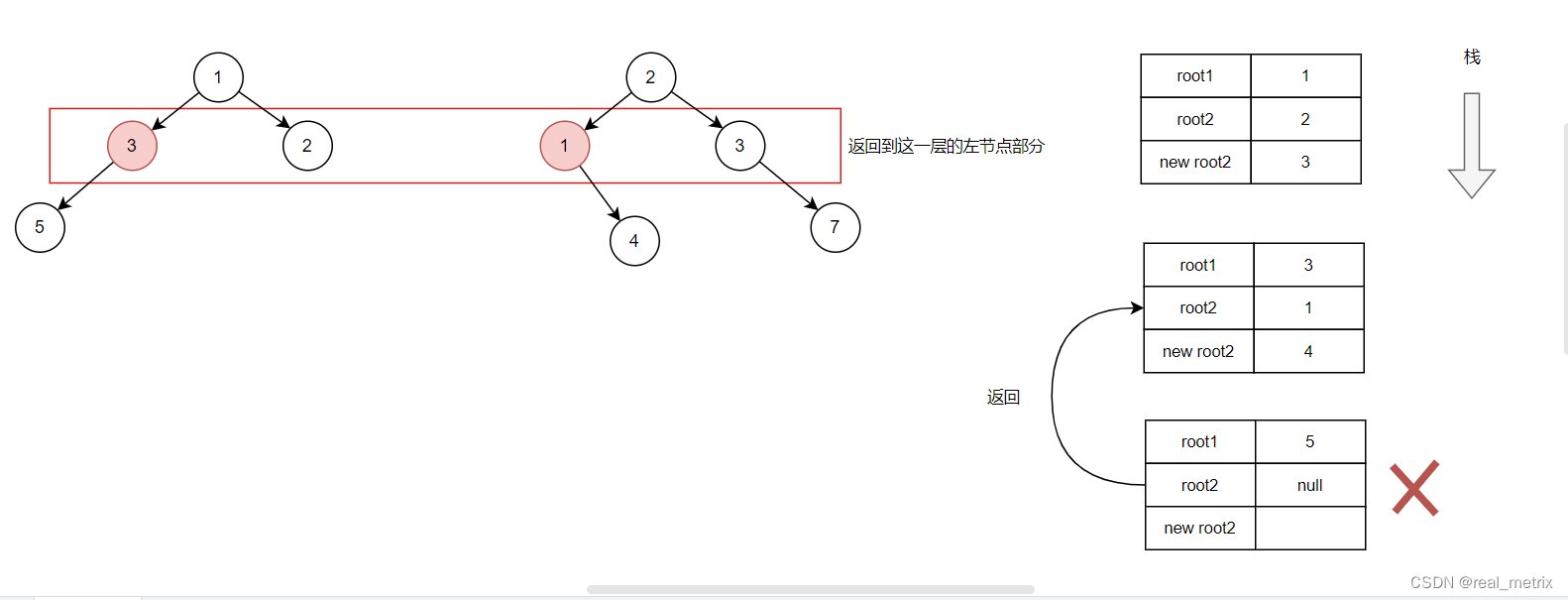
此時左節點已經處理完了，接著處理右節點（即紅色節點的右節點），處理方式同上一步相同。

之后的步驟以此類推就可以完成。

時空復雜度分析

時間復雜度為為 O(n)，n 為節點的個數，空間復雜度為 O(h)，h 為樹的高度，因為每一層樹都要開辟一個新的棧空間