ProlificDreamer 論文閱讀

Project指路：https://ml.cs.tsinghua.edu.cn/prolificdreamer/
論文簡介：截止2023/8/10，text-to-3D的baseline SOTA，提出了VSD優化方法

前置芝士:text-to-3D任務簡介

text-to-3D Problem

text-to-3D 解決的問題就是給定一段話，生成視角一致的3D場景，如果了解過這個領域的可以略過不看

研發路線大概是dreamfeild->dreamfusion->polificdreamer

Diffusion Model

text-to-image領域Diffusion Model很厲害，所以基本上就是Extend Diffusion Model to 3D，想看Diffusion Model簡介可以看我之前的博文：

生成模型的Basic Idea就是真實圖片作為隨機分布，每個text是條件。

• Diffusion Model訓練出了一個條件分布$p(\mathbf{x}|y)$，x是圖片，y是條件（text），其Loss Function可以表達為$${\mathcal{L}}_{Diff}(?):={\mathbb{E}}_{x_0～q(x_0),t～\mathcal{U}(0,1),?～\mathcal{N}(0,1)}[w(t)\Vert {?}_{?}({\alpha }_t{x}_0+{\sigma }_t?)??{\Vert }_2^2]$$

text-to-3D 基本思路

• $\theta$是3D表達的參數，$c$是參數，那么3D渲染的本質是$\mathbf{x}=g(\theta ,c)$，如果過程是可微的，稱為DIP(differentiable image parameterization)
• 對于2D，$x_0～q(x_0)$代表Sample過程，是真實圖片的分布，而text-to-3D就是把Loss變成${\mathcal{L}}_{Diff}(?,\mathbf{x}=g(\theta ,c))$，去優化$\theta$

Prolific Dreamer Basic Idea

符號

• prolific dreamer這篇文章進一步研究，認為一個合理的3D表達也是一個分布，也就是$\theta ～\mu (\theta |y)$
• 渲染出來的圖片：$q_0^{\mu }(x_0|c,y):=\int q_0^{\mu }(x_0|c,y)p(c)dc$
• diffusion model渲染出來的圖片：$p_0(x_0|y)$

優化目標

優化一個參數分布，使得它和Diffusion Model生成的結果接近（pretrained）
$$\underset{\mu }{\min }{D}_{KL}(q_0^{\mu }(x_0|y)\Vert p_0(x_0|y))$$

算法

Loss Function

根據上述優化目標，可以提出如下的Loss

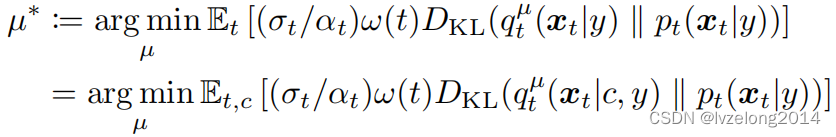
BTW，為什么這個等號成立我是不太理解的（原論文說是KL Divergence的性質），占個坑

我認為這個步驟其實就是cover Diffusion Model的步驟，$q_t^{\mu }(x_t|y):=\int q_0^{\mu }(x_0|c,y)p_{t0}(x_t|x_0)d{x}_0$，也就是給定camera，把某張圖片渲染出來之后拿去上t步高斯噪聲的分布，讓這個分布和Diffsuion Model 第t步的圖片分布盡可能接近。

這已經是一個非常形式化的優化目標了。接下來考慮優化手段。

Optimization

采用Wasserstein gradient flow of VSD，簡單理解就是，用 { θ } i = 1 n \set\theta_{i=1}^n {θ}i=1n?這n個參數“粒子”去模擬$\mu (\theta |y)$，然后優化的時候就是優化每個粒子參數。

基于此，問題轉化解如下的一個ODE：

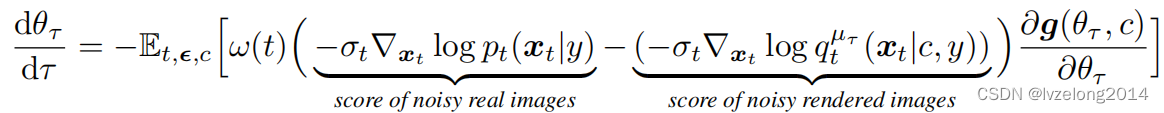
第一項是Diffusion Model生成的帶噪音的真實圖片的score function，所以它由預訓練好的${?}_{pretrain}(x_t,t,y)$生成
第二項是渲染出來圖片生成的帶噪聲的圖片的score function，它由根據一個新網絡${?}_{?}(x_t,t,c,y)$生成，這個網絡采用LoRA 技術，微調${?}_{pretrain}$再embedding一個c進去。

所以進一步轉化：

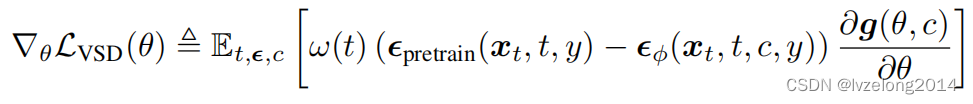
并得到了如下的算法

這篇文章的做法到這里介紹完畢。

數學原理

占坑代填，孩子暫時不會泛函推不了