二、介紹

圖1

????????以上這3張圖片有什么共同點？如果你的猜測是平行線，那么你是對的。這種幾何屬性是藝術家用來在其藝術中呈現 3D 視圖的主要工具。此屬性也是從單眼攝像頭或單個圖像構建 3D 視圖的主要支柱。讓我們在本文中討論這個問題。

????????我通過將圖 3 中存在的第 3 張圖像作為輸入來重建 1D 場景。此實現存在一些縮放和指標校正問題。我會在某個時候解決這個問題。

圖2–從單個圖像進行3D重建

請觀看視頻。

這里的主要思想是如何利用幾何和線性代數從單眼相機或單個圖像重建 3D 視圖。

三、概述

????????從單個圖像進行3D重建主要取決于您如何使用幾何結構從單個圖像或單眼相機獲得K和R值。

相機校準（K）值主要負責將2D點從圖像平面反向投影到3D空間，旋轉（R）值捕獲所有結構之間的旋轉。

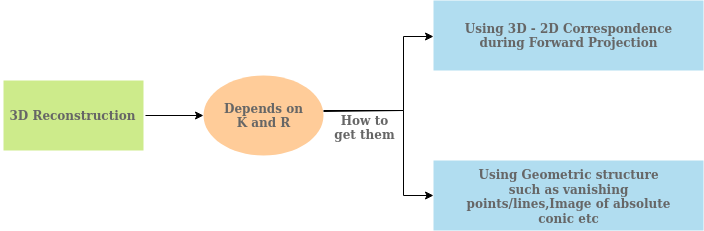
圖3

????????單圖像或單眼相機的3D重建過程通常涉及2步過程

1. 找到 K 和 R
   1.1。使用前向投影。
   1.2. 使用幾何結構。
2. 背投
   這涉及將 2D 圖像點投影到 3D 空間。

四、線性代數

????????讓我們討論一些關于線性代數的基礎知識以及如何使用它們。我想到的基本問題是為什么需要線性代數？簡短的回答是：

幾何結構根據一些線性方程給出了場景中存在的不同點/線/圓錐之間的關系，這就是為什么需要線性代數來求解方程并找到未知數的原因。

????????以下是線性代數的概述。請參考。

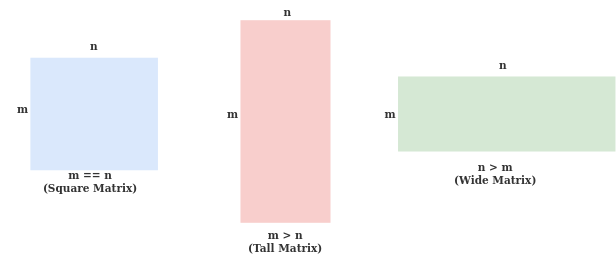
當您設計線性方程組時，它屬于以下類別之一：

• 方形系統（m = n）
• 矩形系統 （m ！=n）- 在確定系統（n > m）- 在確定系統（m > n）
  ?

????????當您使用直接線性變換（DLT）時，非常需要上述理解。

????????我認為有了上述理解，我們可以進入下一階段。

五. 找到 K 和 R ：

5.1. 使用前向投影

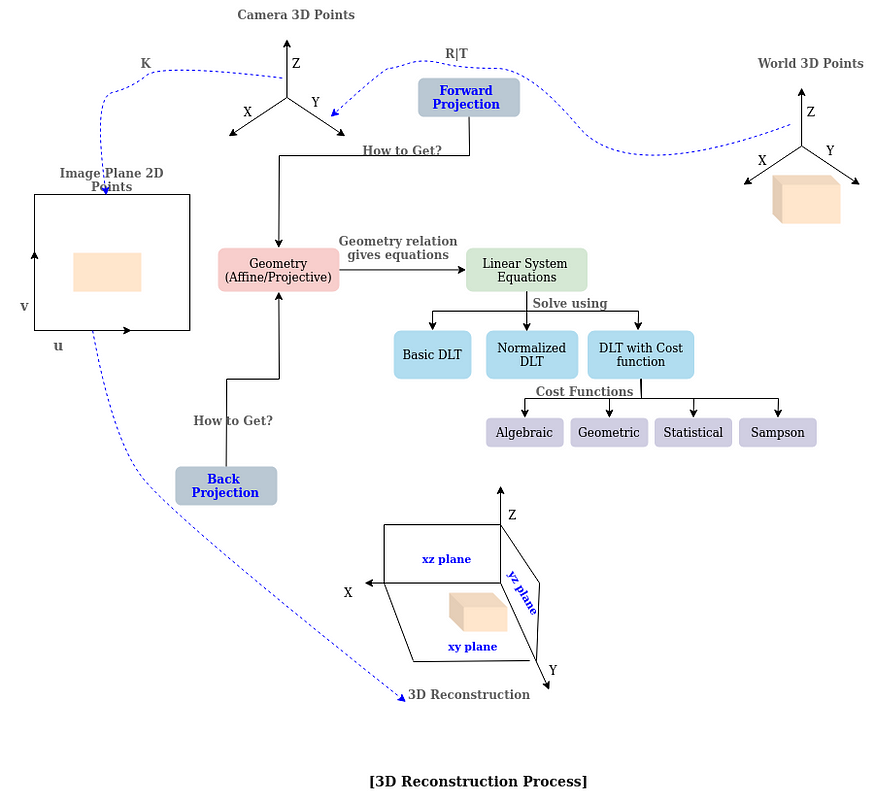
圖5

????????在前向投影中，已知的 3D 點（假設 X）首先將其轉換為相機坐標系，然后轉換為圖像坐標系，從而投影到圖像平面（假設 x）上。整個過程表示為：

x = PX — -等式（1）

其中 P 是 4x3 投影矩陣。P可以分解為KR[I | -C]，其中K=相機校準，R=旋轉，C=相機中心。

如果已知 3D 點和 2D 點，則只需要從方程 （1） 中找到 P。所以我們需要了解P的自由度。

P 具有 11 個自由度（不包括比例因子）。

K = 5，R = 3， C= 3

圖6

如果 P 有 11 個自由度，這意味著它需要 5 個零 1/2 個點來求解線性方程。這是不可能的，所以我們需要拿6分。

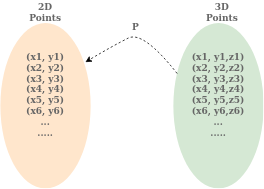
圖7

根據上述計算，n = 11 和 m=12。因此，據說該系統是過度確定的，可以有多個解決方案并且需要近似。參見圖4。

如何使用直接線性變換（DLT）獲得K和R：

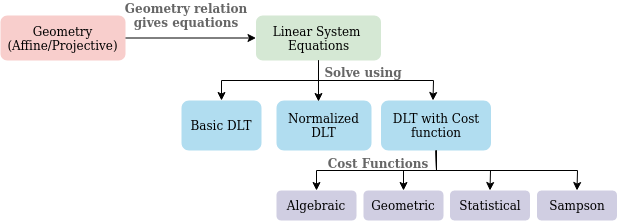
DLT基本上形成了方程PX=0的線性系統，并從中找到K和R。它被歸類為

• 基本 DLT。
• 標準化的 DLT。
  此版本與相機中心的原點不變。因此，它是比基本DLT更受歡迎的一種。
• 具有成本函數的DLT。
  在超定解的情況下，線性系統可以有許多解。因此，我們需要用一些成本函數（例如代數成本）近似解。

在這里，我們只討論基本的DLT。

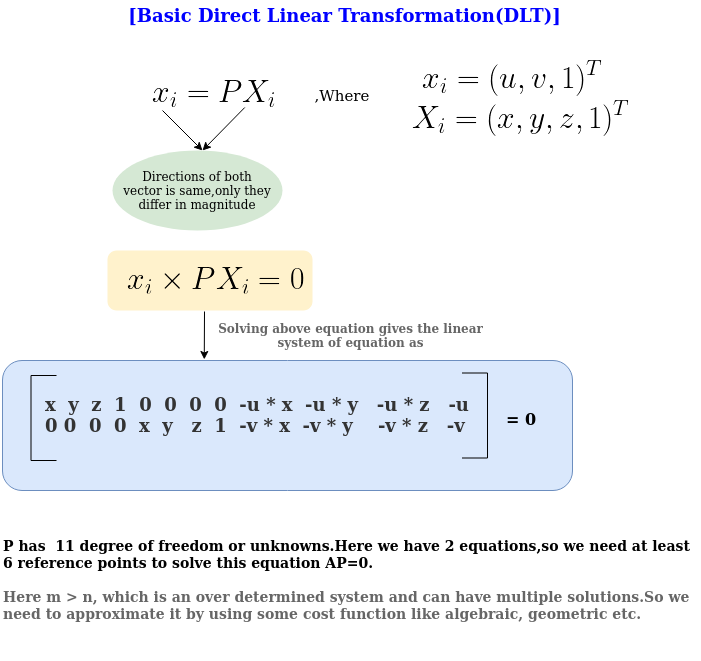
圖8

請檢查?GitHub - satya15july/2d_3d_corespondence?的實現。

5.2. 使用幾何結構：

以下是針孔相機型號中使用的不同幾何形狀的簡短摘要

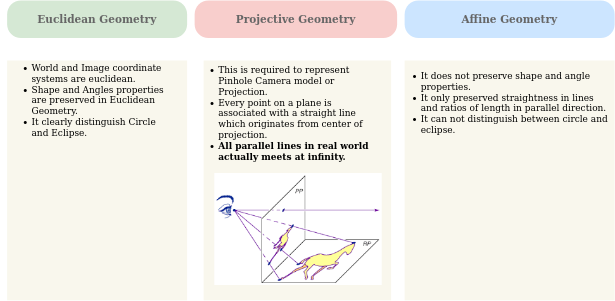
圖10

上述所有幾何形狀均用于針孔相機模型，用于3D圖像重建。

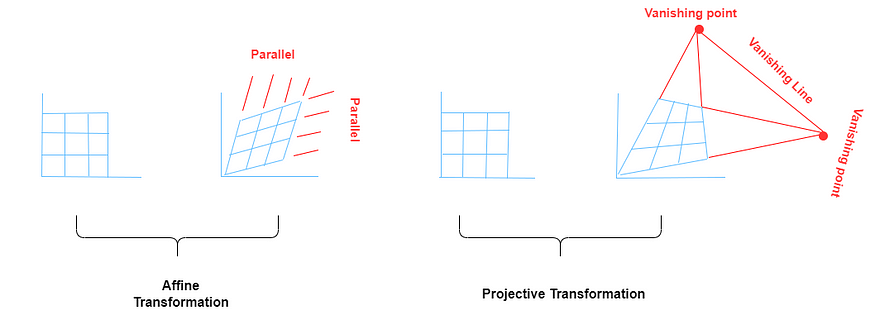
圖11

這是射影幾何、仿射幾何和歐幾里得幾何之間關系的簡化視圖。

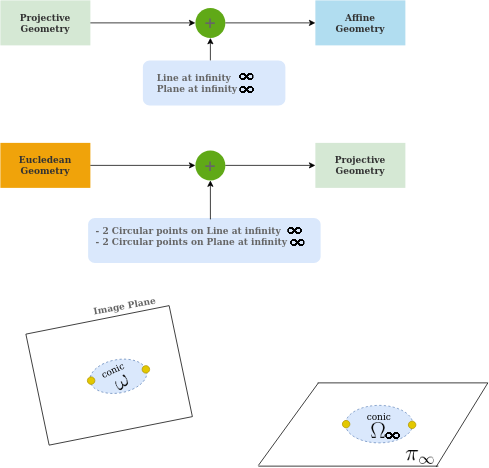
圖12

如何從單視圖幾何中獲取 K 和 R

首先，您需要了解仿射幾何、射影幾何和歐幾里得幾何中存在的一些屬性。

1. 角度屬性不保留在射影幾何或仿射幾何中，但它保留在歐幾里得幾何中。
2. 圓錐和圓在歐幾里得幾何中可以唯一標識，但射影幾何只能識別點，線和圓錐（圓作為圓錐）。
3. 如果要在射影幾何中找到射線或平面或直線之間的角度，則必須識別圓錐或絕對圓錐（IAC）的圖像。原因是
   - 圓錐由歐幾里得幾何和射影幾何確定。
   - 消失線在 2 個圓形點處與錐相交。

以下是從 IAC 獲得 K 和 R 的方法

圖.13

由上圖可知，求K和R的第一步是

• 找到歐米茄（w）。
• 然后，找到 K 和 R。

如何從 3 個正交消失對中獲取 Omega：

如果存在 3 個正交消失點，就可以輕松找到 Omega。請檢查下圖。

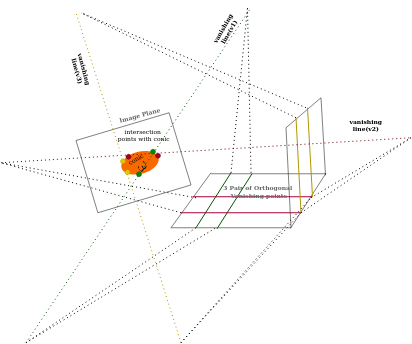
圖.14

????????任何直線都可以與圓錐體/日食相交于 1 或 2 個點。因此消失線最多與圓錐體相交于 2 個點。

????????這里詳細解釋了錐體到歐米伽方程是如何推導的。

????????????????????????????????????????????????????????????????圖15

如果我們可以施加一些額外的約束，例如，

• 如果使用方形像素，則 w1==w3 。
• 如果沒有使用比例因子，則 w2=0

然后歐米茄基質變成

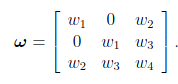
請檢查?GitHub - satya15july/find_K_from_orthogonal_planes?的實現。

從幾何結構中找到歐米茄后，您可以輕松地從中獲得K和R。請參考圖 13。

六、?背投

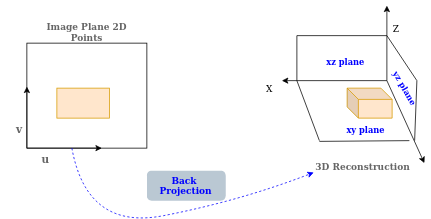
????????????????????????????????????????????????????????????????圖16

讓我們在其他文章中討論這個問題，因為我不想讓這篇文章變得大。

七、結論

????????校準相機意味著K是已知的，我們需要知道R，因為我們需要了解場景中存在的2個結構之間所需的旋轉。在這里，我們了解如何使用不同的方法從單個圖像中找到它們。

現在的問題是，在了解了這種技術之后，我們如何從單個圖像或單眼相機重建3D場景。

檢查下面的圖像或任何隨機的街景，我們如何通過使用上述技術重建它？我們可能需要哪些其他技術。這是一個有趣的問題。解決方案在某個時候再見。

????????讓我們在這里暫停一下，我希望這篇文章能讓您清楚地了解 3D 重建的工作原理。感謝您的閱讀。

????????具體的實現在

• GitHub - satya15july/2d_3d_corespondence。
• GitHub - satya15july/find_K_from_orthogonal_planes。
• GitHub - satya15july/find_K_from_non_othogonal_planes。
• GitHub - satya15july/3dreconstruction_single_image。

????????如果您喜歡這些內容，歡迎拍手，并關注我以獲取有關計算機視覺，3D重建和深度學習的更多信息內容。

引用

• 計算機視覺中的多視圖幾何，作者：Richard Hartley 和 Andrew Zisserman。