灰色關聯分析綜述
諸如經濟系統、生態系統、社會系統等抽象系統都包含許多因素,系統整體的發展受各個因素共同影響。
為了更好地推動系統發展,我們需要清楚哪些因素是主要的,哪些是次要的,哪些是積極的,哪些是消極的,這就要求我們進行系統分析。
數理統計中的系統分析方法包括回歸分析、方差分析和主成分分析,它們都存在一些不足之處,當數據樣本較少時,灰色關聯分析方法可以較好地克服那些不足。
因此,當樣本個數較大時,一般使用標準化回歸;當樣本個數較少時,才使用灰色關聯分析。
灰色關聯分析的基本思想,是根據序列曲線的幾何形狀的相似程度來判斷其聯系是否緊密,曲線越接近,相似序列之間的關聯度就越大,反之就越小。
接下來我們用兩個例題來介紹一下灰色關聯分析的兩種應用。
應用一:進行系統分析

?第一步:畫統計圖并分析
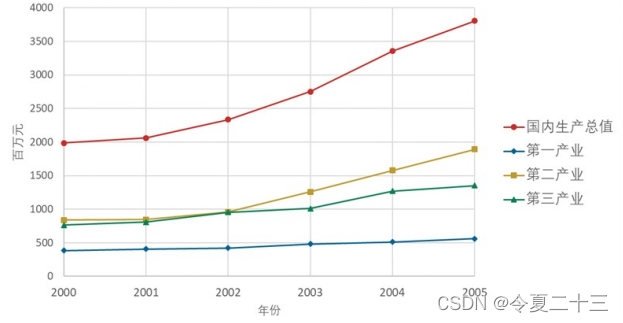
?由圖可知:
- 四個變量均呈上升趨勢;
- 第二產業的增幅較為明顯;
- 第二產業和第三產業的差距在后三年相差更大。
第二步:確定分析數列
母序列(參考數列、母指標):能反映系統行為特征的數據序列。類似于因變量Y,這里記作X0
子序列(比較序列、子指標):影響系統行為的因素組成的數據序列。類似于自變量X,記作X1~Xn
在例題中,國內生產總值就是母序列,第一、第二和第三產業就是子序列。
第三步:對變量進行預處理
目的:去量綱,縮小變量范圍以簡化計算。
對母序列和子序列中的每個指標進行預處理:先求出每個指標的均值,再用該指標的每個元素除以其均值。
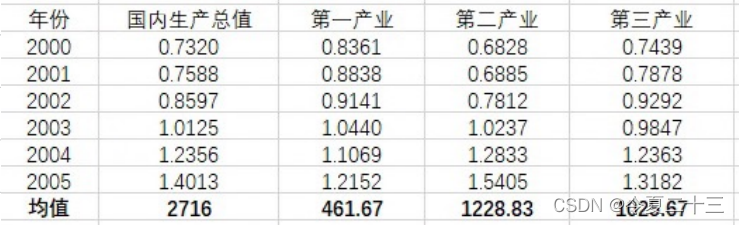
?第四步:計算子序列中各個指標與母序列的關聯系數
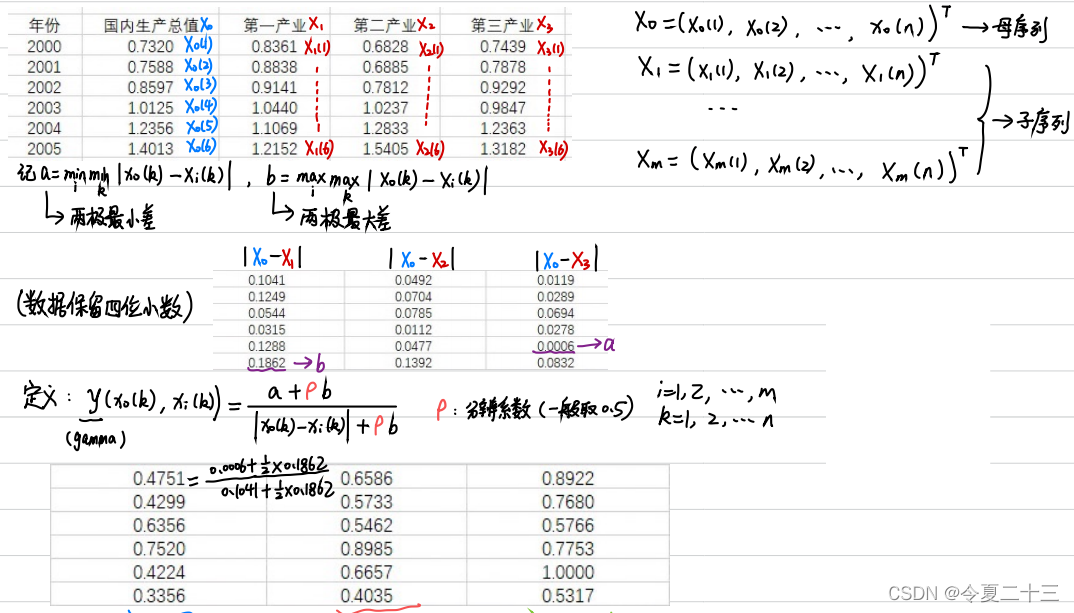
?第五步:求出灰色關聯度
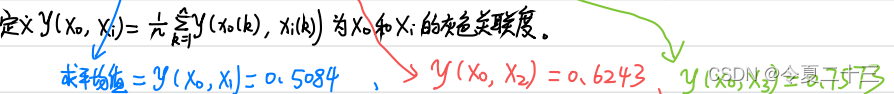
?第六步:比較關聯度,得出結論
對這個例題來說,該地區在2000年至2005年間的國內生產總值受到第三產業的影響最大(其灰色關聯度最大)。
代碼
clear;clc
load gdp.mat % 導入數據 一個6*4的矩陣
Mean = mean(gdp); % 求出每一列的均值以供后續的數據預處理
gdp = gdp ./ repmat(Mean,size(gdp,1),1); %size(gdp,1)=6, repmat(Mean,6,1)可以將矩陣進行復制,復制為和gdp同等大小,然后使用點除(對應元素相除)
disp('預處理后的矩陣為:'); disp(gdp)
Y = gdp(:,1); % 母序列
X = gdp(:,2:end); % 子序列
absX0_Xi = abs(X - repmat(Y,1,size(X,2))) % 計算|X0-Xi|矩陣(在這里我們把X0定義為了Y)
a = min(min(absX0_Xi)) % 計算兩級最小差a
b = max(max(absX0_Xi)) % 計算兩級最大差b
rho = 0.5; % 分辨系數取0.5
gamma = (a+rho*b) ./ (absX0_Xi + rho*b) % 計算子序列中各個指標與母序列的關聯系數
disp('子序列中各個指標的灰色關聯度分別為:')
disp(mean(gamma))
應用二:綜合評價問題
題目:評價下表中20條河流的水質情況。(用Topsis結合熵權法也可以解決)
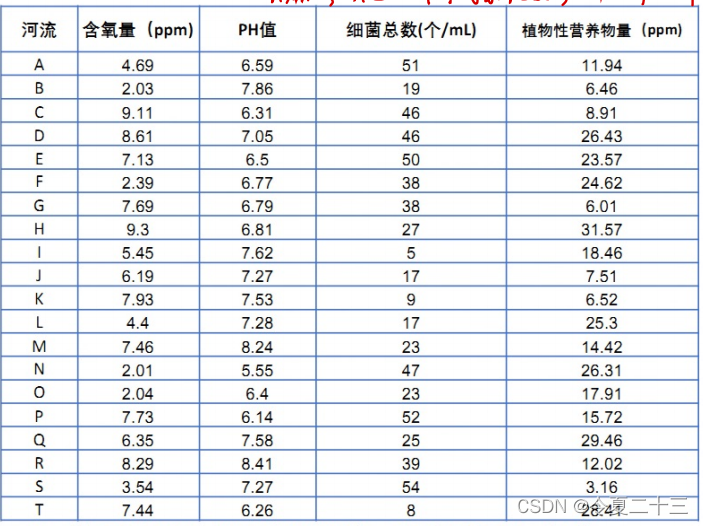
?解題步驟
- 對指標正向化
- 對正向化后的矩陣進行預處理
- 將預處理后的矩陣每一行取出最大值構成母序列
- 計算各個指標與母序列的灰色關聯度
- 計算各個指標灰色關聯度的權重
- 計算各個評價對象的得分(用權重計算)
- 對得分進行歸一化
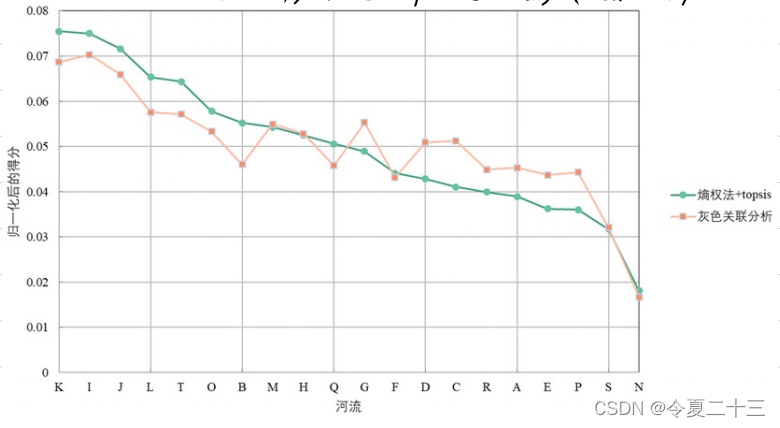

)





)

)









