博主簡介

---

💡一個熱愛分享高性能服務器后臺開發知識的博主，目標是通過理論與代碼實踐的結合，讓世界上看似難以掌握的技術變得易于理解與掌握。技能涵蓋了多個領域，包括C/C++、Linux、Nginx、MySQL、Redis、fastdfs、kafka、Docker、TCP/IP、協程、DPDK等。
👉
🎖? CSDN實力新星、CSDN博客專家、華為云云享專家、阿里云專家博主
👉
👉我的博客將提供以下內容：
👉
💡1. 高性能服務器后臺開發知識深入剖析：深入探討各種技術的原理和內部工作機制，幫助理解它們的核心概念和使用方法。
👉
💡2. 實踐案例與代碼分享：分享一些實際項目中的應用案例和代碼實現，幫助將理論知識轉化為實際應用，并提供實踐中的經驗和技巧。
👉
💡3. 技術教程和指南：編寫簡明扼要的教程和指南，幫助初學者入門并逐步掌握這些技術，同時也為有經驗的開發者提供深入的技術進階指導。
👉
💡無論是一個剛入門的初學者，還是一個有經驗的開發者，我的博客都將提供有價值的內容和實用的技術指導。

---

一、引言

1.1、紅黑樹和AVL樹簡介

紅黑樹和AVL樹都是自平衡二叉搜索樹，它們在維護有序數據集合時非常有用。

紅黑樹： 紅黑樹是一種高效的平衡樹，它是一種近似平衡的二叉搜索樹，在每個節點上都有一個額外的標志來表示節點的顏色（紅色或黑色）。紅黑樹滿足以下規則：

• 節點是紅色或黑色。
• 根節點是黑色。
• 所有葉子節點（NIL節點）都是黑色。
• 如果一個節點是紅色，則其兩個子節點都是黑色。
• 從任意節點到其每個葉子節點的所有路徑都包含相同數目的黑色節點（這保證了樹的近似平衡性）。
  

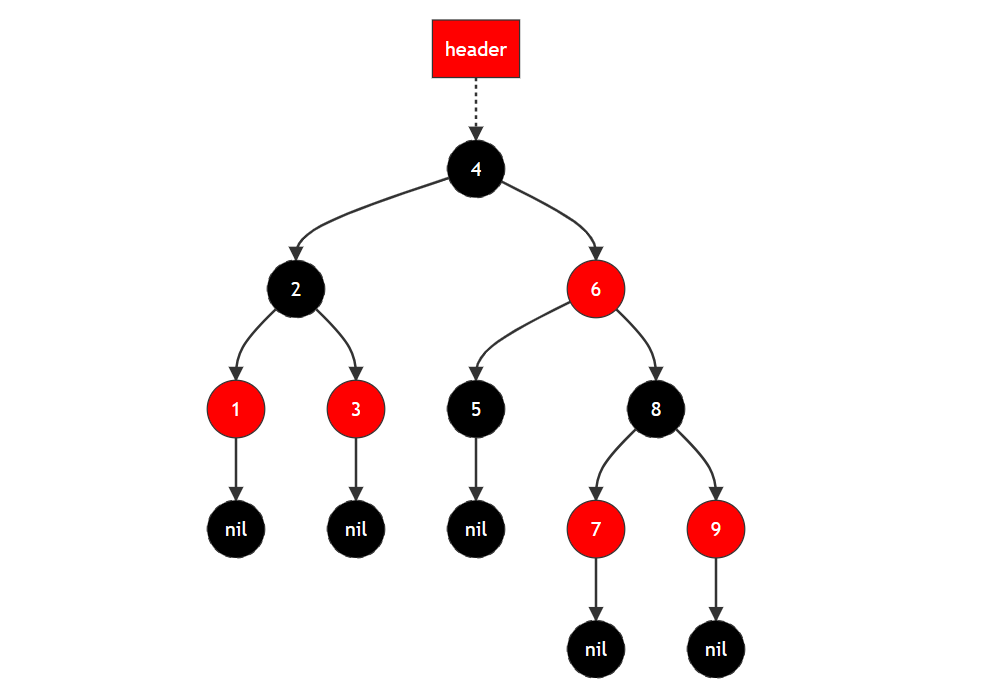
這些規則確保了紅黑樹的平衡性，使得在進行插入和刪除操作時，紅黑樹能夠通過有限次旋轉和重新著色來維護其平衡狀態。紅黑樹在插入和刪除操作上相對較快，但在查找操作的性能上可能略有劣勢。

AVL樹： AVL樹是一種更為嚴格的平衡樹，它的全稱是"Adelson-Velsky and Landis"，得名于其發明者。AVL樹要求在任何節點的左子樹和右子樹高度差不超過1。因為它的平衡條件更為嚴格，所以在進行插入和刪除操作時，AVL樹可能需要更多的旋轉來保持平衡，因此在維護平衡性方面開銷較大。但與此同時，AVL樹在查找操作上可能比紅黑樹更快，因為它的高度比紅黑樹更低。

1.2、紅黑樹在某些方面優于AVL樹

1. 平衡性維護開銷：紅黑樹相對于AVL樹來說，在維護平衡性方面更加輕量級。AVL樹要求每個節點的左子樹和右子樹的高度差不超過1，因此在進行插入和刪除操作時，可能需要更頻繁地進行旋轉操作來維護這種嚴格的平衡性，導致插入和刪除的開銷更大。而紅黑樹通過一系列的規則來保持近似平衡，允許在一定程度上的不平衡，減少了維護平衡性的開銷。

2. 插入和刪除性能：由于紅黑樹放寬了對平衡性的要求，它在進行插入和刪除操作時通常比AVL樹更快。尤其是在頻繁進行大量插入和刪除操作的場景下，紅黑樹相比AVL樹會更高效。

3. 內存占用：紅黑樹通常比AVL樹占用更少的內存空間。由于紅黑樹允許在一定程度上的不平衡，它的高度相對較低，這導致了更少的額外節點和指針。而AVL樹由于要保持嚴格的平衡，可能需要更多的節點和指針來維護樹的結構，從而增加了內存占用。

4. 查找性能：雖然在維護平衡性和插入刪除方面紅黑樹優于AVL樹，但在查找操作上，AVL樹的性能通常優于紅黑樹。由于AVL樹的嚴格平衡性，查找操作的時間復雜度較低，比紅黑樹更快。

紅黑樹在某些場景下可以提供更好的插入和刪除性能以及更低的內存占用，適用于需要頻繁插入和刪除操作，而對查找性能要求相對較低的情況。然而，對于需要高效查找操作的場景，AVL樹可能更適合，因為它在查找性能上優于紅黑樹。在實際應用中，根據具體的需求來選擇合適的樹結構是很重要的。

二、紅黑樹和AVL樹的基本原理

2.1、紅黑樹的定義和性質

紅黑樹是一種自平衡的二叉查找樹，它在二叉查找樹的基礎上增加了額外的性質來保持樹的平衡。這種自平衡的特性使得紅黑樹的插入、刪除和查找操作的時間復雜度都能夠保持在 $O(logn)$級別。

紅黑樹的定義：

1. 每個節點都有一個顏色，要么是紅色，要么是黑色。
2. 根節點必須是黑色。
3. 葉子節點（NIL 節點）都是黑色的。
4. 如果一個節點是紅色的，則其子節點必須是黑色的。
5. 從任意節點到其每個葉子節點的路徑上，經過的黑色節點數量必須相同。

紅黑樹的性質：

• 從根節點到葉子節點的最長可能路徑不超過最短可能路徑的兩倍。這確保了紅黑樹的高度始終保持在 O(log n) 級別，從而保持了其高效的插入、刪除和查找操作。
• 因為根節點是黑色的，所以紅黑樹沒有根節點到葉子節點全為紅色的路徑。
• 每個葉子節點都是黑色的（通常使用 NIL 節點表示），這樣可以確保空指針問題。
• 如果一個節點是紅色的，它的兩個子節點都是黑色的。這意味著不存在兩個連續的紅色節點，從而避免了出現紅色節點的連續路徑，保持了樹的平衡。
• 從任意節點到其每個葉子節點的路徑上，經過的黑色節點數量必須相同。這個性質保證了紅黑樹在插入和刪除操作后能夠自動調整，重新保持平衡。

紅黑樹的這些性質共同保證了樹的平衡性和高效性。在插入和刪除節點時，紅黑樹會根據這些性質進行自我調整，通過顏色變換和樹的旋轉操作來保持性質的滿足，從而保持了樹的平衡。這些自平衡的操作確保了紅黑樹的搜索、插入和刪除操作都能夠保持在 $O(logn)$ 的時間復雜度，使得紅黑樹成為一種廣泛應用于數據結構和算法中的二叉查找樹。

2.2、AVL樹的定義和性質

AVL樹是一種自平衡的二叉搜索樹，它的定義和性質如下：

定義：AVL樹是一種二叉搜索樹，其中每個節點的左子樹和右子樹的高度差（平衡因子）不超過1。

性質：

• AVL樹是一棵二叉搜索樹，所以它滿足二叉搜索樹的性質：對于每個節點，它的左子樹的所有節點都小于該節點的值，右子樹的所有節點都大于該節點的值。
• 每個節點的平衡因子等于其右子樹的高度減去左子樹的高度。平衡因子只能是-1、0或1，否則不滿足AVL樹的定義。
• AVL樹中的每個子樹也是AVL樹，這意味著在插入或刪除節點后，整棵樹需要通過旋轉操作來保持平衡。

AVL樹的自平衡特性保證了樹的高度保持較小，使得查找、插入和刪除操作的時間復雜度都能夠保持在O(log n)。然而，由于其頻繁的自平衡操作，相比于紅黑樹，AVL樹可能會在某些場景下有更高的常數時間開銷。

2.3、對比兩種樹結構的特點

平衡性要求：

• 紅黑樹：對于紅黑樹，它允許節點的左右子樹高度差在一定范圍內（不超過2倍），而不是像AVL樹那樣嚴格要求平衡因子不超過1。這使得紅黑樹的平衡要求相對較寬松。

• AVL樹：AVL樹要求任何節點的左右子樹高度差不超過1，這是一種嚴格的平衡性要求。

插入和刪除操作：

• 紅黑樹：由于紅黑樹的平衡性要求相對較松，插入和刪除操作相對較快。當執行插入和刪除時，紅黑樹可能需要進行少量的旋轉和重新著色操作來維持平衡。

• AVL樹：AVL樹的平衡性要求更嚴格，因此在插入和刪除操作時，可能需要進行多次旋轉來保持樹的平衡。這使得插入和刪除操作相對較慢。

搜索性能：

• 紅黑樹：由于紅黑樹的平衡性要求較松，它的高度可能相對較高。這可能導致搜索操作的性能略低于AVL樹。

• AVL樹：由于AVL樹的嚴格平衡性要求，它的高度相對較小，因此搜索性能較好。

紅黑樹示意圖：

AVL樹示意圖：

三、插入和刪除操作的復雜性比較

3.1、紅黑樹的插入操作和平衡性維護

1. 插入節點：首先按照二叉搜索樹的規則，將新節點插入到紅黑樹中，通常將新節點標記為紅色。

2. 重新著色和旋轉：為了維護紅黑樹的平衡性，需要對插入的節點進行著色和旋轉操作。

• a. 若插入節點的父節點是黑色，則不會破壞紅黑樹的性質，插入后樹依然保持平衡。

• b. 若插入節點的父節點是紅色，則需要進一步考慮調整。

• c. 當插入節點的叔節點（父節點的兄弟節點）也是紅色時，需要進行重新著色，將父節點和叔節點設為黑色，祖父節點設為紅色，并將祖父節點作為當前節點繼續處理。

• d. 當插入節點的叔節點是黑色或者缺失時，需要進行旋轉操作。

例如：

3. 旋轉操作：旋轉操作主要包括左旋和右旋。
   

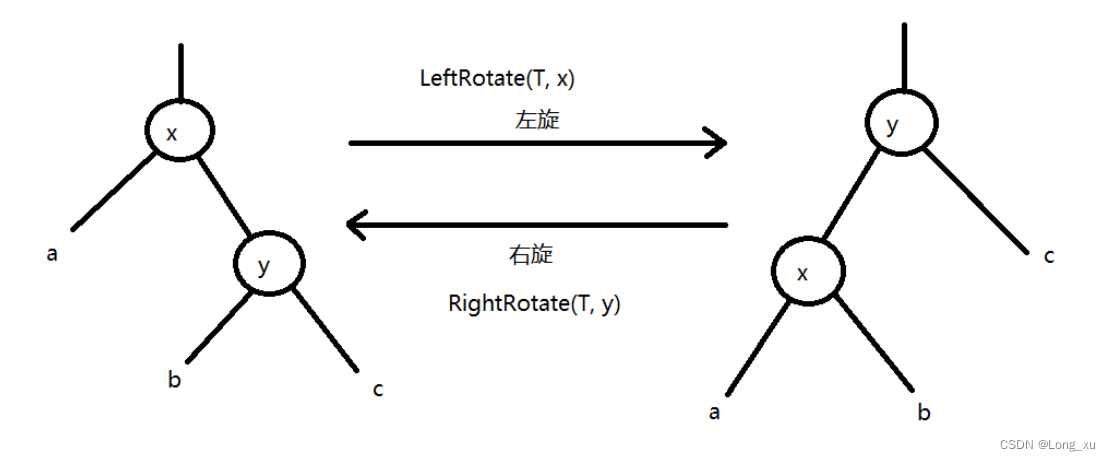
• a. 左旋：當插入節點在父節點的右子樹中，且插入節點的父節點和祖父節點都為紅色時，需要進行左旋操作，以保持平衡。

• b. 右旋：當插入節點在父節點的左子樹中，且插入節點的父節點和祖父節點都為紅色時，需要進行右旋操作，以保持平衡。

3.2、AVL樹的插入操作和平衡性維護

AVL樹是一種自平衡二叉搜索樹，與紅黑樹類似，它也需要在插入操作后保持平衡性。AVL樹通過旋轉操作來維護平衡性，但與紅黑樹不同的是，AVL樹使用不同類型的旋轉：左旋、右旋、左右旋、右左旋。

AVL樹的插入操作和平衡性維護步驟如下：

1. 插入新節點：首先按照二叉搜索樹的規則將新節點插入到AVL樹中。

2. 自底向上更新高度：從插入點開始，沿著插入路徑向上更新所有父節點的高度，直到達到根節點。AVL樹的高度是左子樹高度和右子樹高度中較大值加1。

3. 檢查平衡因子：在更新高度后，從插入點向上檢查每個節點的平衡因子，平衡因子定義為節點的左子樹高度減去右子樹高度。

4. 平衡維護：如果發現某個節點的平衡因子不滿足平衡性要求（平衡因子的絕對值大于1），則需要進行相應的旋轉操作來重新平衡這個節點的子樹。

• a. 左旋（LL旋轉）：當一個節點的左子樹高度比右子樹高度多2或以上時，且插入操作發生在左子樹的左子樹（左-左情況），執行左旋操作。

• b. 右旋（RR旋轉）：當一個節點的右子樹高度比左子樹高度多2或以上時，且插入操作發生在右子樹的右子樹（右-右情況），執行右旋操作。

• c. 左右旋（LR旋轉）：當一個節點的左子樹高度比右子樹高度多2或以上時，且插入操作發生在左子樹的右子樹（左-右情況），執行左旋后再執行右旋操作。

• d. 右左旋（RL旋轉）：當一個節點的右子樹高度比左子樹高度多2或以上時，且插入操作發生在右子樹的左子樹（右-左情況），執行右旋后再執行左旋操作。

注意：每次進行旋轉后，需要更新涉及節點的高度。

5. 遞歸：完成旋轉后，可能會影響到更上層節點的平衡性，所以需要繼續向上檢查和遞歸地執行旋轉操作，直到達到根節點。

6. 最終平衡：在整個插入和旋轉操作完成后，AVL樹的平衡性得到維護。

圖解示例：

原始AVL樹（平衡因子用數字表示）：

插入節點 3：

插入節點 2，破壞平衡：

由于節點 5 的平衡因子為 2，需要進行旋轉操作來恢復平衡。進行左旋轉：

最終平衡的AVL樹：

與紅黑樹相比，AVL樹的平衡性維護相對嚴格，因為它要求節點的左右子樹高度差不能超過1。這也使得在插入操作頻繁的情況下，紅黑樹的性能可能更優，因為紅黑樹在犧牲一定的平衡性的前提下，保證了插入和刪除操作的時間復雜度為O(logN)。而AVL樹的旋轉操作可能會頻繁地觸發，導致額外的開銷。

3.3、分析并對比兩種樹在插入操作中的性能差異

紅黑樹（Red-Black Tree）和AVL樹（Adelson-Velsky and Landis Tree）都是自平衡二叉搜索樹，用于保持樹的平衡性以保證各種操作（插入、刪除、查找等）的時間復雜度在較低的范圍內。然而，它們在自平衡的方式和性能方面有一些不同之處，特別是在插入操作中。

自平衡策略不同：

• 紅黑樹： 紅黑樹通過維護五個重要的性質來保持平衡，其中包括節點的顏色（紅色或黑色）和一些限制條件，確保了從根到任意葉子節點的最長路徑不會超過最短路徑的兩倍。插入操作可能會引發顏色變換和旋轉操作來保持這些性質。

• AVL樹： AVL樹通過在每個節點上維護一個平衡因子（左子樹高度減去右子樹高度）來保持平衡。插入操作可能會導致旋轉操作，以使平衡因子保持在特定的范圍內，通常是-1、0或1。

插入操作性能：

• 紅黑樹： 由于紅黑樹的自平衡策略相對較為寬松，插入操作的性能一般來說會比AVL樹更好。雖然插入后可能需要進行顏色變換和旋轉，但是這些操作的數量較少，平均情況下仍然能夠維持較低的時間復雜度。
• AVL樹： AVL樹對于插入操作來說是相對嚴格的，因為它要求保持平衡因子的絕對值不超過1。這意味著在插入操作后，可能需要進行更多的旋轉操作來調整樹的結構，以滿足平衡要求。這可能會導致插入操作的性能相對較差，尤其是在頻繁插入的情況下。

在插入操作方面，紅黑樹通常比AVL樹具有更好的性能。但需要注意的是，性能差異在不同情況下可能會有所變化，因為實際性能還受到其他因素的影響，如具體的插入順序、硬件性能等。

3.3.1、實現一個AVL樹進行一萬次數據插入

#include <stdio.h>
#include <stdlib.h>
#include <sys/time.h>
// AVL樹節點結構
struct Node {int key;struct Node* left;struct Node* right;int height;
};// 獲取節點的高度
int getHeight(struct Node* node) {if (node == NULL) {return 0;}return node->height;
}// 獲取兩個整數中的較大值
int max(int a, int b) {return (a > b) ? a : b;
}// 創建新節點
struct Node* newNode(int key) {struct Node* node = (struct Node*)malloc(sizeof(struct Node));node->key = key;node->left = NULL;node->right = NULL;node->height = 1;return node;
}// 右旋操作
struct Node* rightRotate(struct Node* y) {struct Node* x = y->left;struct Node* T2 = x->right;x->right = y;y->left = T2;y->height = max(getHeight(y->left), getHeight(y->right)) + 1;x->height = max(getHeight(x->left), getHeight(x->right)) + 1;return x;
}// 左旋操作
struct Node* leftRotate(struct Node* x) {struct Node* y = x->right;struct Node* T2 = y->left;y->left = x;x->right = T2;x->height = max(getHeight(x->left), getHeight(x->right)) + 1;y->height = max(getHeight(y->left), getHeight(y->right)) + 1;return y;
}// 獲取平衡因子
int getBalanceFactor(struct Node* node) {if (node == NULL) {return 0;}return getHeight(node->left) - getHeight(node->right);
}if (node == NULL) {return newNode(key);}   if (key < node->key) {node->left = insert(node->left, key);} else if (key > node->key) {node->right = insert(node->right, key);} else {return node; // 不允許插入相同的鍵值}   node->height = 1 + max(getHeight(node->left), getHeight(node->right));int balance = getBalanceFactor(node);// 左-左情況if (balance > 1 && key < node->left->key) {return rightRotate(node);}   // 右-右情況if (balance < -1 && key > node->right->key) {return leftRotate(node);}   // 左-右情況if (balance > 1 && key > node->left->key) {node->left = leftRotate(node->left);return rightRotate(node);}   // 右-左情況if (balance < -1 && key < node->right->key) {node->right = rightRotate(node->right); return leftRotate(node);}   return node;
}   // 獲取樹的高度
int treeHeight(struct Node* node) {if (node == NULL) {return 0;}return node->height;
}int main() {struct Node* root = NULL;struct timeval start_time, end_time;long long start_microseconds, end_microseconds, elapsed_microseconds;// 獲取起始時間gettimeofday(&start_time, NULL);start_microseconds = start_time.tv_sec * 1000000 + start_time.tv_usec;// 進行10000次插入操作for (int i = 1; i <= 10000; i++) {root = insert(root, i);}// 獲取結束時間gettimeofday(&end_time, NULL);end_microseconds = end_time.tv_sec * 1000000 + end_time.tv_usec;// 計算時間差elapsed_microseconds = end_microseconds - start_microseconds;printf("Time taken: %lld microseconds\n", elapsed_microseconds);// 打印樹的高度printf("樹的高度: %d\n", treeHeight(root));return 0;
}

執行結果：

Time taken: 2498 microseconds
樹的高度: 14

3.3.2、實現一個紅黑樹進行一萬次數據插入

#include <stdio.h>
#include <stdlib.h>
#include <sys/time.h>
typedef enum Color {RED,BLACK
} Color;typedef struct Node {int data;Color color;struct Node* parent;struct Node* left;struct Node* right;
} Node;Node* createNode(int data) {Node* newNode = (Node*)malloc(sizeof(Node));newNode->data = data;newNode->color = RED; // New nodes are always red initiallynewNode->parent = NULL;newNode->left = NULL;newNode->right = NULL;return newNode;
}void leftRotate(Node** root, Node* x) {Node* y = x->right;x->right = y->left;if (y->left != NULL) {y->left->parent = x;}y->parent = x->parent;if (x->parent == NULL) {*root = y;} else if (x == x->parent->left) {x->parent->left = y;} else {x->parent->right = y;}y->left = x;x->parent = y;
}void rightRotate(Node** root, Node* y) {Node* x = y->left;y->left = x->right;if (x->right != NULL) {x->right->parent = y;}x->parent = y->parent;if (y->parent == NULL) {*root = x;} else if (y == y->parent->left) {y->parent->left = x;} else {y->parent->right = x;}x->right = y;y->parent = x;
}void insertFixup(Node** root, Node* z) {while (z->parent != NULL && z->parent->color == RED) {if (z->parent == z->parent->parent->left) {Node* y = z->parent->parent->right;if (y != NULL && y->color == RED) {z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent;} else {if (z == z->parent->right) {z = z->parent;leftRotate(root, z);}z->parent->color = BLACK;z->parent->parent->color = RED;rightRotate(root, z->parent->parent);}} else {Node* y = z->parent->parent->left;if (y != NULL && y->color == RED) {z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent;} else {if (z == z->parent->left) {z = z->parent;rightRotate(root, z);}z->parent->color = BLACK;z->parent->parent->color = RED;leftRotate(root, z->parent->parent);}}}(*root)->color = BLACK;
}void insert(Node** root, int data) {Node* z = createNode(data);Node* y = NULL;Node* x = *root;while (x != NULL) {y = x;if (z->data < x->data) {x = x->left;} else {x = x->right;}}z->parent = y;if (y == NULL) {*root = z;} else if (z->data < y->data) {y->left = z;} else {y->right = z;}insertFixup(root, z);
}void inorderTraversal(Node* root) {if (root != NULL) {inorderTraversal(root->left);printf("%d ", root->data);inorderTraversal(root->right);}
}int max(int a, int b) {return (a > b) ? a : b;
}int blackHeight(Node* node) {if (node == NULL)return 1;int leftHeight = blackHeight(node->left);int rightHeight = blackHeight(node->right);if (leftHeight == 0 || rightHeight == 0 || leftHeight != rightHeight)return 0;return leftHeight + ((node->color == BLACK) ? 1 : 0);
}int getBlackHeight(Node* root) {if (root == NULL)return 0;return blackHeight(root->left);
}int main() {Node* root = NULL;struct timeval start_time, end_time;long long start_microseconds, end_microseconds, elapsed_microseconds;// 獲取起始時間gettimeofday(&start_time, NULL);start_microseconds = start_time.tv_sec * 1000000 + start_time.tv_usec;// 進行10000次插入操作for (int i = 1; i <= 10000; i++) {insert(&root, i);}// 獲取結束時間gettimeofday(&end_time, NULL);end_microseconds = end_time.tv_sec * 1000000 + end_time.tv_usec;// 計算時間差elapsed_microseconds = end_microseconds - start_microseconds;printf("Time taken: %lld microseconds\n", elapsed_microseconds);// printf("Inorder traversal of the Red-Black Tree:\n");// inorderTraversal(root);// printf("\n");int height = getBlackHeight(root);printf("Black height of the Red-Black Tree: %d\n", height);return 0;
}

執行結果：

Time taken: 2494 microseconds
Black height of the Red-Black Tree: 12

3.4、紅黑樹相對于AVL樹的優勢

紅黑樹和AVL樹都是自平衡二叉搜索樹，它們在保持二叉搜索樹的性質的同時，通過旋轉和節點操作來保持樹的平衡。雖然它們都有類似的目標，但在某些方面紅黑樹相對于AVL樹有一些優勢，主要體現在以下幾點：

• 插入和刪除操作的效率： 紅黑樹相對于AVL樹的主要優勢之一是在插入和刪除操作上更為高效。紅黑樹的平衡要求相對較松，因此插入和刪除操作可能需要更少的旋轉，從而減少了平衡操作的次數。而AVL樹由于平衡要求較為嚴格，可能需要更頻繁的旋轉來維持平衡，導致插入和刪除操作相對較慢。

• 空間開銷： 紅黑樹相對于AVL樹在存儲平衡信息方面具有優勢。紅黑樹只需要一個比特來存儲節點的顏色信息（紅或黑），而AVL樹需要存儲每個節點的平衡因子，通常需要更多的空間。

• 查詢性能： 在純粹的查詢操作上，AVL樹可能略微優于紅黑樹，因為AVL樹的平衡要求更嚴格，可能導致樹更加扁平，從而在某些情況下查找效率略高。

四、查找和遍歷操作的效率比較

4.1、紅黑樹的查找和遍歷操作

紅黑樹是一種平衡的二叉搜索樹。其查找和遍歷操作與普通的二叉搜索樹類似，但是由于紅黑樹的特性，其最壞的查找時間復雜度是O(log n)。

（1）查找操作: 查找操作在紅黑樹中非常簡單。如果我們要查找一個值k，我們可以從根節點開始：

• 如果k等于當前節點的值，查找成功。
• 如果k小于當前節點的值，轉到左子樹。
• 如果k大于當前節點的值，轉到右子樹。
• 如果當前節點為空，則查找失敗。

Node* search(Node* root, int k) {while (root != NULL) {if (k == root->data)return root;else if (k < root->data)root = root->left;elseroot = root->right;}return NULL; // Value not found
}

（2）遍歷操作: 紅黑樹的遍歷可以分為前序、中序和后序遍歷，與普通二叉搜索樹的遍歷方法相同。

• 中序遍歷（In-order）: 左子樹 -> 當前節點 -> 右子樹
• 前序遍歷（Pre-order）: 當前節點 -> 左子樹 -> 右子樹
• 后序遍歷（Post-order）: 左子樹 -> 右子樹 -> 當前節點

例如，中序遍歷的代碼可以是這樣的：

void inorderTraversal(Node* root) {if (root == NULL)return;inorderTraversal(root->left);printf("%d ", root->data);inorderTraversal(root->right);
}

4.2、AVL樹的查找和遍歷操作

（1）查找操作：

1. 步驟1：從根節點開始，與待查找值進行比較。
2. 步驟2：如果待查找值等于當前節點的值，則返回該節點。
3. 步驟3：如果待查找值小于當前節點的值，則繼續在左子樹中遞歸查找。
4. 步驟4：如果待查找值大于當前節點的值，則繼續在右子樹中遞歸查找。
5. 步驟5：如果遍歷完整個樹仍未找到相應節點，則說明該節點不存在。

typedef struct Node {int value;struct Node* left;struct Node* right;int height;
} Node;Node* search(Node* root, int target) {if (root == NULL || target == root->value) {return root;}if (target < root->value) {return search(root->left, target);}return search(root->right, target);
}

（2）遍歷操作：

• 前序遍歷：根節點 -> 左子樹 -> 右子樹
• 中序遍歷：左子樹 -> 根節點 -> 右子樹
• 后序遍歷：左子樹 -> 右子樹 -> 根節點

void preorderTraversal(Node* root) {if (root != NULL) {printf("%d ", root->value);preorderTraversal(root->left);preorderTraversal(root->right);}
}void inorderTraversal(Node* root) {if (root != NULL) {inorderTraversal(root->left);printf("%d ", root->value);inorderTraversal(root->right);}
}void postorderTraversal(Node* root) {if (root != NULL) {postorderTraversal(root->left);postorderTraversal(root->right);printf("%d ", root->value);}
}

4.3、對比兩種樹在查找和遍歷操作中的性能差異

（1）查找操作：
平均情況下，紅黑樹和AVL樹的查找操作都具有O(log n)的時間復雜度，其中n是樹中節點的數量。這是由于它們都是二叉搜索樹結構，每次查找可以通過比較節點的鍵值來確定目標節點的位置，并且樹的平衡性質保證了查找路徑的長度接近樹的高度。

（2）遍歷操作：
前序、中序和后序遍歷對于紅黑樹和AVL樹而言，在時間復雜度上沒有顯著差異。這是因為無論是紅黑樹還是AVL樹，遍歷操作都需要訪問每個節點一次，并以相同的順序輸出節點的值，所以它們的時間復雜度都是O(n)，其中n是樹中節點的數量。

紅黑樹和AVL樹在查找和遍歷操作的性能方面沒有太大差異。它們的主要區別在于維護平衡的方式和性質要求。

五、內存占用和空間復雜性比較

5.1、紅黑樹的內存占用特點

紅黑樹相對于其他平衡樹結構來說，在內存占用方面有以下特點：

• 相對于AVL樹：紅黑樹在保持樹的平衡性方面，放寬了平衡要求，通過一些特定的性質來維持近似平衡。這使得紅黑樹的高度可能稍微比AVL樹更大，因此紅黑樹可能需要更多的內存空間來存儲相同數量的節點。

• 比較其他平衡樹結構：相對于一些其他平衡樹結構，如B樹或B+樹等，紅黑樹通常會占用更多的內存空間。紅黑樹中每個節點都需要保存顏色信息（一般使用一個額外的位來表示紅色或黑色），而其他平衡樹結構可能只需要保存鍵值和指針信息。

紅黑樹相對于其他平衡樹結構在內存占用方面可能略高，但其在平衡性和時間復雜度上的優勢使得它依然是一個被廣泛使用的數據結構。

5.2、AVL樹的內存占用特點

相對于其他平衡樹結構，AVL樹在內存占用方面有以下特點：

1. 節點結構：AVL樹的每個節點通常需要保存鍵值、指向左右子樹的指針以及平衡因子（即左右子樹的高度差）。這些額外的信息會增加每個節點的內存消耗。

2. 平衡因子：AVL樹中的平衡因子可以是一個整數或枚舉類型，需要額外的空間來存儲。一般情況下，平衡因子使用8位或更少的比特位表示，所以占用的額外內存很小。

3. 平衡維護：AVL樹為了維持平衡性，可能需要進行旋轉操作來調整樹的結構。這些旋轉操作本身并不會引入額外的內存消耗，但在執行旋轉操作過程中需要使用一些臨時變量，這些臨時變量的內存開銷可能較小。

AVL樹相對于其他平衡樹結構來說，在內存占用方面沒有顯著的差異。它們都需要為每個節點保存一定的鍵值和指針信息，并且可能需要一些額外的信息來維持平衡。真正影響內存占用的因素更多地取決于具體實現的細節，例如節點結構的大小和平衡因子的表示方式等。

5.3、對比兩種樹在內存占用和空間復雜性方面的優勢

（1）內存占用：

• AVL樹相對于紅黑樹來說，每個節點需要額外存儲平衡因子來維持嚴格的平衡。這使得AVL樹在內存占用上略高于紅黑樹。
• 紅黑樹相對于AVL樹來說，由于放寬了平衡要求，不需要額外存儲平衡因子。因此，在相同數量的節點下，紅黑樹的總體內存占用可能略低于AVL樹。

空間復雜性：

• 平均情況下，紅黑樹和AVL樹在插入、刪除和查找操作的時間復雜度都是O(log n)，其中n是樹中節點的數量。這意味著它們在空間復雜性上沒有顯著差異。

• 但是，紅黑樹相對于AVL樹有更松散的平衡要求，可以忍受一定程度的不平衡，因此在頻繁地插入和刪除操作時，紅黑樹可能更具優勢，因為其自平衡操作的代價較低。

紅黑樹和AVL樹在內存占用和空間復雜性方面有不同的優勢：

• AVL樹在內存占用上可能稍高，但在查找操作上更穩定且具備嚴格的平衡性。
• 紅黑樹在內存占用上相對較低，且適合于頻繁的插入和刪除操作。

六、性能優化和應用場景

6.1、如何根據具體應用場景選擇合適的樹結構

（1）二叉搜索樹 (BST)：

• 優點：適用于快速查找、插入和刪除操作。中序遍歷可以得到有序序列。
• 適用場景：當需要頻繁進行查找和動態插入/刪除操作時。然而，原始的BST可能會變得不平衡，導致性能下降。

（2）AVL樹：

• 優點：自平衡的BST，保證了樹的高度較小，因此查找、插入和刪除操作的時間復雜度都保持在對數級別。
• 適用場景：當需要高效的平衡樹結構，以確保各種操作的穩定性能時。但由于自平衡操作可能會帶來一些額外開銷，因此在插入和刪除操作頻繁的情況下，可能會略微降低性能。

（3）紅黑樹：

• 優點：與AVL樹類似，是一種自平衡的BST，但相對于AVL樹，紅黑樹的自平衡操作更簡單，插入和刪除操作的代價較小。
• 適用場景：在需要保持相對平衡的同時，對于插入和刪除操作的性能要求較高的場景。

（3）B樹和B+樹：

• 優點：這些樹結構被設計用于在磁盤等外部存儲上進行高效的數據存儲和檢索。B樹適合隨機訪問，B+樹適合范圍查詢。
• 適用場景：數據庫索引、文件系統等需要在外部存儲上組織數據的場景。

（4）Trie樹（前綴樹）：

• 優點：適用于高效地存儲和查找字符串數據。特別適合用于搜索和自動補全等字符串相關的應用。
• 適用場景：字典、搜索引擎、拼寫檢查等需要處理字符串的場景。

（5）堆：

• 優點：用于高效地獲取最大或最小元素。堆排序、優先隊列等算法基于堆實現。
• 適用場景：調度算法、最短路徑算法、動態選取最值等需要優先級管理的場景。

在選擇合適的樹結構時，要考慮數據操作的頻率、特點，以及數據的插入、刪除和查找等操作的性能需求。沒有一種樹結構適用于所有情況。。

6.2、紅黑樹的優化策略

1. 局部性優化：在進行插入、刪除等操作時，可以盡量減少樹的旋轉和重新著色操作，以降低操作的開銷。例如，在插入元素時，可以通過旋轉和著色操作來保持樹的平衡，但不一定非得追求完美平衡，可以在一定程度上容忍一些不平衡，從而減少調整的次數。

2. 批量操作：如果需要執行大量的插入或刪除操作，可以采用一種叫做“延遲刪除”的策略。即，先將要刪除的節點標記為刪除而不立即刪除它，而是等到執行一次大規模調整操作時再一并刪除，這樣可以減少頻繁的調整操作。

3. 自適應調整：根據實際數據的特點和操作模式，可以動態地調整某些操作的策略。例如，對于頻繁訪問的節點，可以將它們置于樹的較淺層，以加快訪問速度。

4. 優化旋轉操作：在紅黑樹的插入和刪除過程中，可能需要進行旋轉操作來保持平衡。優化旋轉操作的方式包括路徑壓縮（將中間節點向上移動，減少旋轉操作的次數）和雙旋轉等。

5. 緩存友好性：在實際應用中，可以考慮紅黑樹的節點布局，使得相鄰節點在內存中也是相鄰的，以提高緩存的命中率，從而加速樹的訪問。

6. 擴展功能：根據實際需求，可以對紅黑樹進行一些功能擴展，例如添加范圍查詢、區間更新等操作，以滿足特定場景下的需求。

6.3、AVL樹的優化策略

雖然AVL樹本身已經具備較好的平衡性能，但在某些特定的應用場景下，仍然可以考慮一些優化策略來進一步提高性能。

• 延遲更新：在AVL樹的插入和刪除操作中，可能會涉及多次旋轉來保持平衡，這會帶來一些性能開銷。延遲更新策略可以在一次操作結束后，再進行平衡因子的更新和旋轉操作，從而減少不必要的操作次數。

• 局部重構：在插入和刪除操作中，如果發現某個節點的平衡因子超過了允許的范圍，可以考慮對該節點及其祖先節點進行局部重構，以避免多次單旋轉。這可以減少整體的旋轉次數，提高性能。

• 批量操作：如果需要對AVL樹進行一系列的插入或刪除操作，可以將這些操作批量執行，然后再一次性進行平衡操作。這樣可以減少多次單獨操作帶來的開銷，提高整體效率。

• 局部性優化：類似于紅黑樹中的緩存友好性，可以考慮優化AVL樹節點的布局，使得相鄰節點在內存中也是相鄰的。這有助于提高緩存的命中率，加速樹的訪問。

• 自適應調整：根據實際應用中的數據分布和操作頻率，可以考慮調整平衡因子的閾值，使得樹的平衡調整更加自適應，從而在不同情況下都能保持較好的性能。

6.4、實際應用中紅黑樹勝過AVL樹的案例和場景

• 插入和刪除操作頻繁的情況：紅黑樹的平衡因子要求相對寬松一些，相比AVL樹更容易維護平衡，這在頻繁執行插入和刪除操作的場景下可能會表現更好。例如，文件系統中的目錄結構維護、數據庫的索引維護等。

• 讀操作遠多于寫操作的情況：紅黑樹的平衡調整次數相對較少，因此在讀取操作明顯多于寫入操作的場景中，紅黑樹可能更適合，因為它不會頻繁執行復雜的平衡旋轉操作，從而減少了開銷。

• 內存限制下的應用：AVL樹因為需要維護嚴格的平衡，可能會導致樹的高度相對較低，這在存儲大量數據時可能占用更多的內存。而紅黑樹在平衡和內存占用之間有更好的權衡，適用于內存有限的環境。

• 實時應用：在需要快速的插入和刪除操作的實時應用中，紅黑樹的平衡特性可能更適合，因為它可以在一定程度上保持樹的相對平衡，避免頻繁的旋轉操作。

紅黑樹和AVL樹都有各自的優勢和劣勢，并且選擇合適的數據結構要根據具體的應用需求來決定。在某些情況下，紅黑樹可能更適合，但在其他情況下，AVL樹可能表現更好。最終的選擇應該基于性能需求、內存限制以及具體操作的頻率和類型來進行權衡。

總結

在文章中，著重比較紅黑樹和AVL樹在插入、刪除、查找、遍歷以及內存占用等方面的性能，指出紅黑樹在某些應用場景下優于AVL樹。同時，還將探討兩種樹的優化策略和實際應用案例。

紅黑樹相對于AVL樹的綜合優勢主要體現在以下幾個方面：

• 插入和刪除操作的性能： 紅黑樹在保持相對平衡的同時，對于插入和刪除操作的性能表現通常優于AVL樹。雖然AVL樹的平衡性更為嚴格，但在插入和刪除時需要更頻繁地進行旋轉操作，而紅黑樹通過放寬平衡要求，減少了旋轉的次數，從而在實際應用中可能更快速地處理這些操作。

• 內存占用： 紅黑樹相對于AVL樹在維護平衡時要求更少的額外信息，因此通常會占用更少的內存。這使得紅黑樹在內存有限的情況下表現更優。

• 實時應用： 在需要快速插入和刪除操作的實時應用中，紅黑樹的平衡特性可能更適合，因為它可以在一定程度上維護樹的平衡性，避免過度頻繁的平衡操作。

• 適應性： 紅黑樹的相對寬松的平衡要求使得它對于動態變化的數據集更具有適應性。當數據集的變化幅度較大，而不僅僅是順序插入時，紅黑樹可能更容易維持相對平衡。

在這里插入圖片描述