給你一個用無限二維網格表示的花園，每一個 整數坐標處都有一棵蘋果樹。整數坐標 (i, j) 處的蘋果樹有 |i| + |j| 個蘋果。

你將會買下正中心坐標是 (0, 0) 的一塊 正方形土地 ，且每條邊都與兩條坐標軸之一平行。

給你一個整數 neededApples ，請你返回土地的 最小周長 ，使得 至少 有 neededApples 個蘋果在土地 里面或者邊緣上。

|x| 的值定義為：

如果 x >= 0 ，那么值為 x
如果 x < 0 ，那么值為 -x

示例 1：

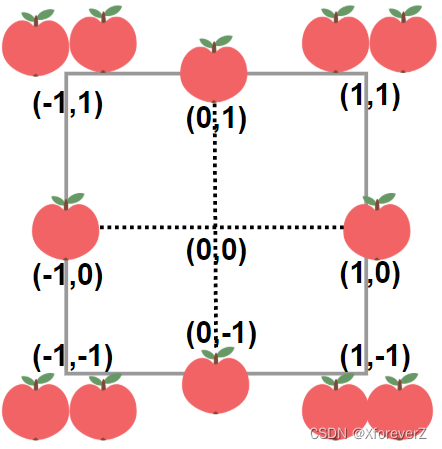
輸入：neededApples = 1
輸出：8
解釋：邊長長度為 1 的正方形不包含任何蘋果。
但是邊長為 2 的正方形包含 12 個蘋果（如上圖所示）。
周長為 2 * 4 = 8 。

示例 2：

輸入：neededApples = 13
輸出：16

示例 3：

輸入：neededApples = 1000000000
輸出：5040

提示：

1 <= neededApples <= 10¹⁵

枚舉這個方法在lc官解：收集足夠蘋果的最小花園周長了解到的，開始做確實沒有想到數學解法，發現了規律但是數學太差,用二分做的：

class Solution {
public:long long minimumPerimeter(long long neededApples) {long long n = 1;for(; 2 * n * (n + 1) * (2 * n + 1) < neededApples; n++);return n * 8;}
};

同樣還有二分的方法但我的代碼wa了幾個（菜狗一個），下面是正確的二分代碼：

class Solution {
public:long long minimumPerimeter(long long neededApples) {long long maxS = 100000;long long le = 0, ri = min(maxS, neededApples);while(le < ri) {long long mid = (le + ri) / 2;if(cal(mid) < neededApples) le = mid+1;else ri = mid;}return 8 * le;}long long cal(long n){return 4*n*n*n + 6*n*n + 2*n;}
};