十大排序總結（js實現、穩定性、內外部排序區別、時間空間復雜度、冒泡、快速、直接選擇、堆、直接插入、希爾、桶、基數、歸并、計數排序）

目錄

排序相關概念

穩定性

?內部排序

外部排序

?十種排序算法特點總結

交換排序

冒泡排序（數組sort方法的原理）

圖解

?js實現

特點

快速排序

圖解

js實現

特點

選擇排序

直接選擇排序

圖解

?js實現

特點

堆排序

大（小）頂堆

非葉節點

js實現?

特點

插入排序?

直接插入排序

圖解

js實現?

特點

希爾排序

圖解

js實現

特點

其它排序

桶排序

圖解

js實現

特點

基數排序

圖解

js實現

特點

歸并排序

圖解

?js實現

特點

計數排序

圖解

?js實現

特點


排序相關概念


穩定性

不改變相同數值的順序為穩定。例如在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，則稱這種排序算法是穩定的(記錄的相對次序保持不變)；否則稱為不穩定的。


?內部排序

指待排序列完全存放在內存中所進行的排序過程，適合不太大的元素序列。有冒泡、選擇、插入、希爾、快速、堆排序（通常快速排序為最好的）。


外部排序

外部排序指的是大文件的排序，即待排序的記錄存儲在外存儲器上，待排序的文件無法一次裝入內存，需要在內存和外部存儲器之間進行多次數據交換，以達到排序整個文件的目的。有歸并、計數、桶、基數排序。


?十種排序算法特點總結


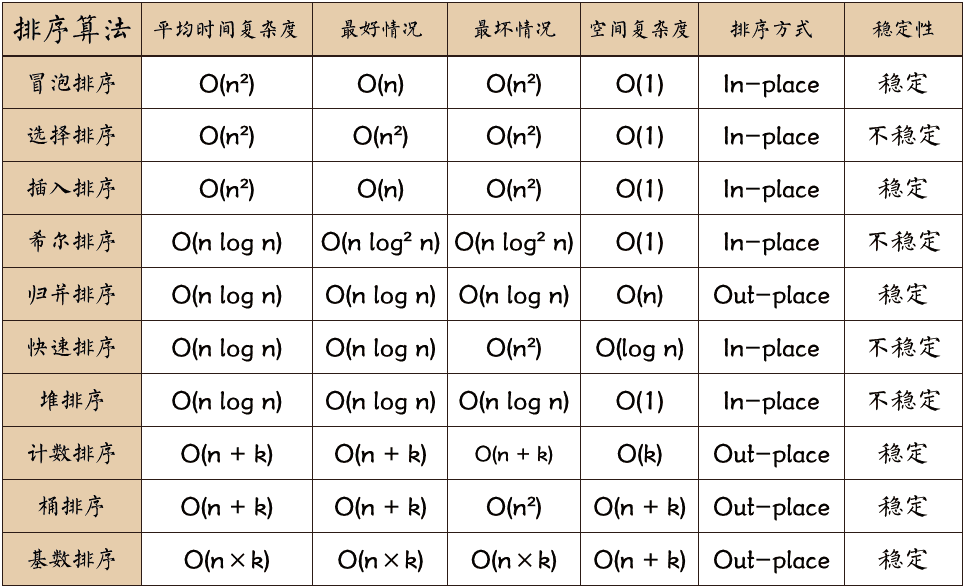
交換排序


冒泡排序（數組sort方法的原理）

1.比較相鄰的元素。如果第一個比第二個大，就交換他們兩個。

2.對每一對相鄰元素作同樣的工作，從開始第一對到結尾的最后一對。這步做完后，最后的元素會是最大的數。

3.針對所有的元素重復以上的步驟，除了最后一個。

4.持續每次對越來越少的元素重復上面的步驟，直到沒有任何一對數字需要比較。


圖解


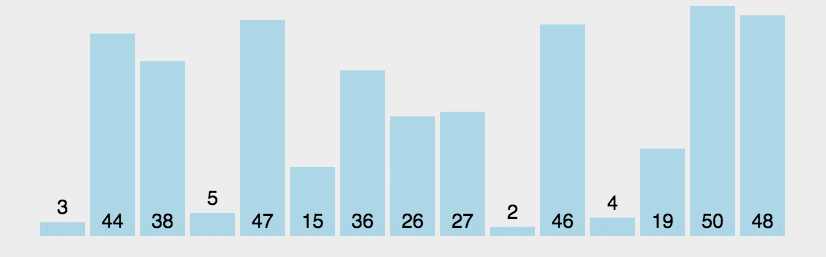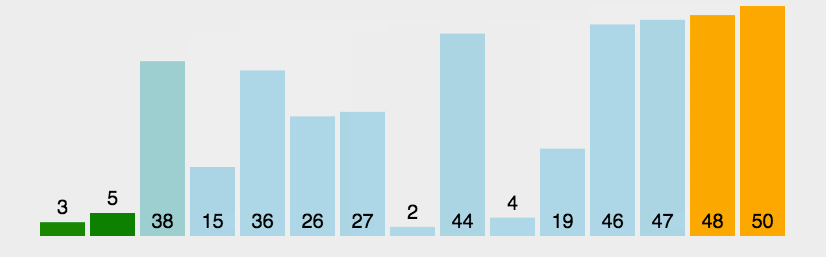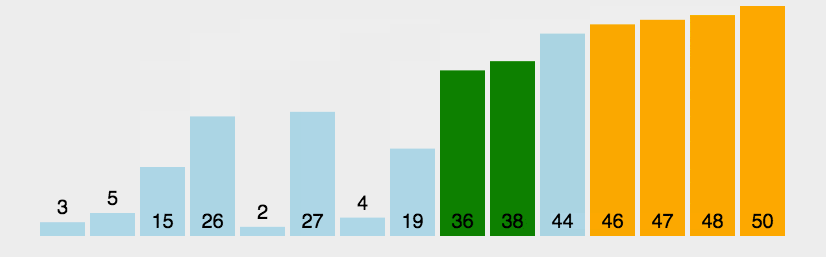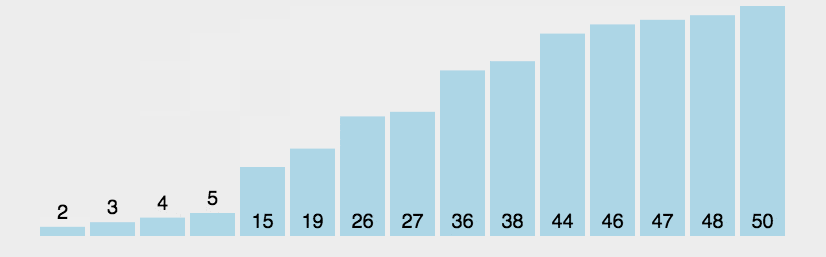
?js實現

function swap(arr, x, y) {let tmp = arr[x]arr[x] = arr[y]arr[y] = tmp
}
function bubbleSort(arr) {let len = arr.length;for (let i = 0; i < len - 1; i++) {//比較出一輪中的最大值放入最后for (let j = 0; j < len - 1 - i; j++) {if (arr[j] > arr[j + 1]) {swap(arr, j, j + 1)}}}return arr;
}


特點

  1. 時間復雜度：O(N^2)
  2. 空間復雜度：O(1)
  3. 穩定性：穩定


快速排序

1.以數組第一位為基準值，將小于的元素放在左邊，大于的元素放在右邊，分為左右兩塊。

2.在左右2塊中重復第一步，不斷循環，直到分區的大小為1則停止。


圖解

注意左右分區，我們可以通過將基準元素和左邊分區最右端元素交換實現


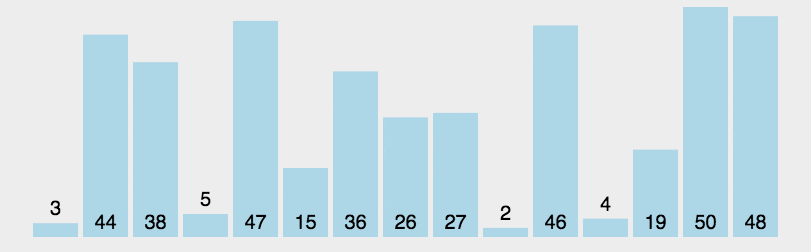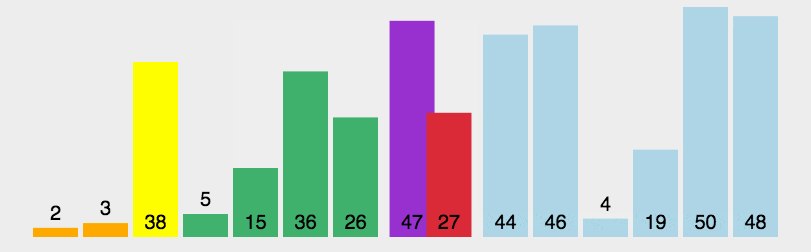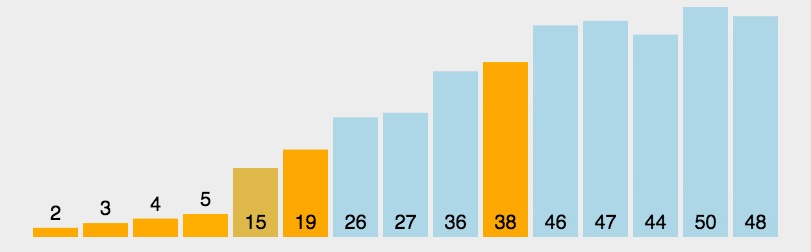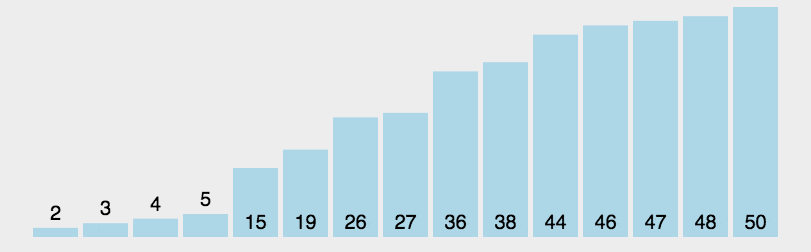
js實現

function swap(arr, x, y) {let tmp = arr[x]arr[x] = arr[y]arr[y] = tmp
}
//用于一次以基準值進行排序
function partition(arr, left, right) {//設定基準值pivotlet pivot = leftlet index = pivot + 1for (let i = index; i <= right; i++) {//小于基準值的放左邊，大于的不變if (arr[i] < arr[pivot]) {swap(arr, i, index)index++}}//和小于基準值的最右邊一個交換位置，實現左邊小于基準值，右邊大于基準值swap(arr, pivot, index - 1)//返回基準值的位置return index - 1
}
function quickSort(arr, left, right) {let len = arr.lengthleft = typeof left != 'number' ? 0 : leftright = typeof right != 'number' ? len - 1 : rightif (left < right) {//進行一次排序let partitionIndex = partition(arr, left, right)//遞歸對左邊進行排序quickSort(arr, left, partitionIndex - 1)//遞歸對右邊進行排序quickSort(arr, partitionIndex + 1, right)}return arr
}
console.log(quickSort([3, 1, 2, 3134, 113, 342, 123412, 55, 111, 4, 234, 5, 5]))


特點

  1. 時間復雜度：O(N*logN)
  2. 空間復雜度：O(logN)
  3. 穩定性：不穩定


選擇排序



直接選擇排序

每一次遍歷待排序的數據元素從中選出最小（或最大）的一個元素，存放在序列的起始（或者末尾）位置（和原存放位置上的元素交換順序），直到全部待排序的數據元素排完。


圖解


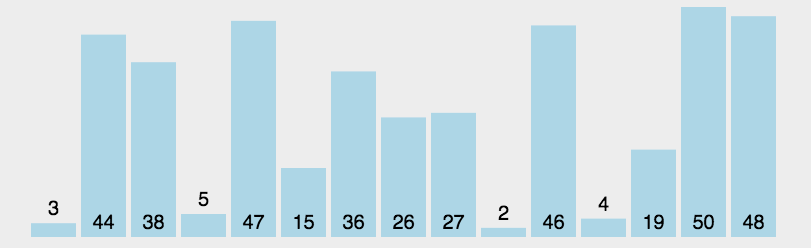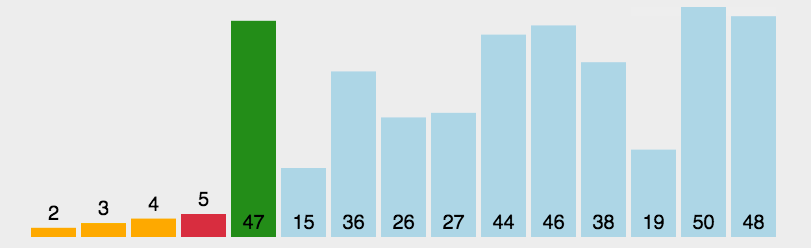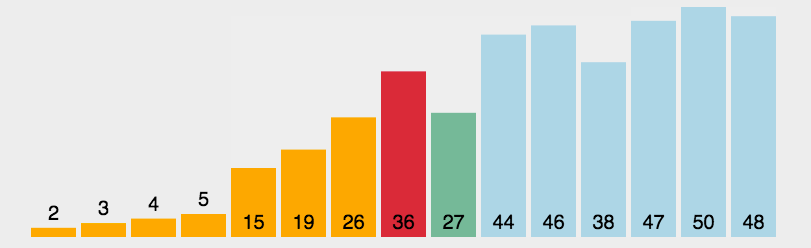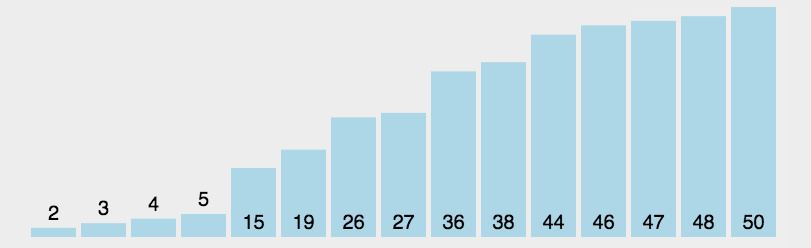
?js實現

//交換數組下標x位和y位的元素
function swap(arr, x, y) {arr[x] = arr[x] - arr[y]arr[y] = arr[y] + arr[x]arr[x] = arr[y] - arr[x]return arr
}
function selectionSort(arr) {let t = arr.lengthlet x = 0while (x != t) {let min = 0;let tmp = Number.MAX_VALUE//選出最小的元素的下標for (let i = x; i < t; i++) {if (tmp > arr[i]) {tmp = arr[i]min = i}}//不是當前位置，則交換順序if (x != min) {swap(arr, x, min)}x++}return arr
}
console.log(selectionSort([3, 1, 2, 3134, 113, 342, 123412, 55, 111, 4, 234, 5, 5]))


特點

  1. 時間復雜度：O(N^2)
  2. 空間復雜度：O(1)
  3. 穩定性：不穩定


堆排序

1.將元素排序為一個大（小）頂堆，則頂部元素為最大（小）元素，將其與元素尾（頭）部元素交換順序。

2.重新排序剩下元素，再次形成大（小）頂堆，重復1操作，直到只剩一個元素。


大（小）頂堆

每個節點的值都大于（小于）或等于其子節點的值，在堆排序算法中用于升（降）序排列；

代碼中表示為：

大頂堆arr[i]>=arr[2i+1]和arr[i]>=arr[2i+2]????????父節點大于左右子節點

小頂堆arr[i]<=arr[2i+1]和arr[i]<=arr[2i+2]?????????父節點小于左右子節點


非葉節點

有孩子節點的節點。最后一個非葉節點在數組中的序號為元素個數除以2向下取整。


js實現?

// 建立大頂堆
function buildMaxHeap(arr) {let len = arr.length;//Math.floor(len/2)表示最后一個非葉節點（含有子節點的節點），//從后往前調整每一個非葉子節點的順序，使堆變為大頂堆for (let i = Math.floor(len / 2); i >= 0; i--) {heapify(arr, i, len);}
}
// 調整堆
function heapify(arr, i, len) {let left = 2 * i + 1,right = 2 * i + 2,largest = i;//通過2次判斷選出父節點和2個子節點中最大的一個if (left < len && arr[left] > arr[largest]) {largest = left;}if (right < len && arr[right] > arr[largest]) {largest = right;}//將最大的節點和父節點交換順序if (largest != i) {swap(arr, i, largest);//遞歸對換順序的節點進行調整，使其還是大頂堆heapify(arr, largest, len);}
}
function swap(arr, i, j) {var temp = arr[i];arr[i] = arr[j];arr[j] = temp;
}
function heapSort(arr) {// 建立大頂堆buildMaxHeap(arr);let len = arr.length//每次建立一個大頂堆，將最大的元素（堆頂元素）放入尾部達到排序效果for (let i = len - 1; i > 0; i--) {swap(arr, 0, i);len--;heapify(arr, 0, len);}return arr;
}
console.log(heapSort([3, 1, 2, 3134, 113, 342, 123412, 55, 111, 4, 234, 5, 5]))


特點

  1. 時間復雜度：O(N*logN)
  2. 空間復雜度：O(1)
  3. 穩定性：不穩定


插入排序?


直接插入排序

每次從無序表中取出第一個元素，把它插入到有序表的合適位置，使有序表仍然有序（默認是從后向前比較）。


圖解

藍色部分為無序表，黃色部分為有序表：

在這里插入圖片描述


js實現?

使用的是一個數組，將數組下標為i之前的為有序，之后為無序。

?注意用的是改變原數組的方法，可以不用返回。

//將數組下標為的x元素取出插入為y的
function popInsert(arr,x,y){arr.splice(y,0,...arr.splice(x,1))
}
function insertSort(arr){let t=arr.lengthfor (let i=1;i<t;i++){let j=i-1do{if(arr[j]<arr[i]){popInsert(arr,i,j+1)break}j--//比較到下標為0的時候直接插入if(j<0){popInsert(arr,i,0)}}while(j>=0)}return arr
}
console.log(insertSort([3,1,2,3134,113,342,123412,55,111,4,234,5,5]))


特點

  1. 元素集合越接近有序，直接插入排序算法的時間效率越高
  2. 時間復雜度：O(N^2)
  3. 空間復雜度：O(1)，它是一種穩定的排序算法
  4. 穩定性：穩定


希爾排序

希爾排序在直接排序之前，進行預排列，將某些極端數據更快的排列到數列前面，構成一個接近排列好的序列，最后再進行一次直接插入排序。

預排列的原理也是插入排列，只不過這里的將數組分成了gap組，分別對每一個小組進行插入排序。


圖解

對于升序，當gap從5 – 2 – 1的過程中，排在后面的數值小的數能更快排到前面，當gap為1的時候實際上就是進行了一次插入排序


在這里插入圖片描述


js實現

每次將下標位置差為gap的數進行直接排序，其中第一次gap=Math.floor(arr.length/2)，之后每次gap=Math.floor(gap/2)。

function shellsSort(arr){let t=arr.lengthlet gap=tlet tmp//gap取不同值的排序do{//每次的分組gap=Math.floor(gap/2)for(let i=gap;i<t;i++){//只和上一個間距為gap的元素進行比較，判斷是否要插入，還是維持原順序if(arr[i-gap]>arr[i]){tmp = arr[i]let j=i-gap//將插入位置之后的元素整體后移do{arr[j+gap]=arr[j]j-=gap}while(j>=0&&arr[j]>tmp)//插入對應位置arr[j+gap]=tmp}}}while(gap>1)return arr
}
console.log(shellsSort([3,1,2,3134,113,342,123412,55,111,4,234,5,5]))


特點

  1. 希爾排序是對直接插入排序的優化當gap > 1時都是預排序，目的是讓數組更接近于有序。當gap == 1時，數組已經接近有序的了，這樣就會很快。這樣整體而言，可以達到優化的效果。我們實現后可以進行性能測試的對比
  2. 希爾排序的時間復雜度不好計算，因為gap的取值方法很多，一般來說為O(n^1.3)?
  3. 穩定性：不穩定


其它排序


桶排序

選出待排序元素中的最大最小值，根據最大最小值劃分多個區域（桶），通過映射函數將元素分到不同區域（桶）中，對區域（桶）中的元素進行排序后，依次取出即可。


圖解

將排序的元素放入對應的桶中

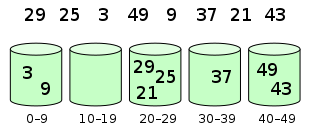
?對桶中的元素進行排序


js實現

//插入排序
function insertionSort(arr) {let len = arr.length;let preIndex, current;for (let i = 1; i < len; i++) {preIndex = i - 1;current = arr[i];while (preIndex >= 0 && arr[preIndex] > current) {arr[preIndex + 1] = arr[preIndex];preIndex--;}arr[preIndex + 1] = current;}return arr;
}
function bucketSort(arr, bucketSize) {let minValue = arr[0];let maxValue = arr[0];//找到數組中的最大和最小值for (let i = 1; i < arr.length; i++) {if (arr[i] < minValue) {minValue = arr[i];} else if (arr[i] > maxValue) {maxValue = arr[i];}}//桶的初始化let DEFAULT_BUCKET_SIZE = 5;// 設置一個桶能存儲的默認數量為5bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;//桶的個數let bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;let buckets = new Array(bucketCount);for (let i = 0; i < buckets.length; i++) {buckets[i] = [];}//利用映射函數將元素分配到各個桶中for (let i = 0; i < arr.length; i++) {buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);}//刪除arr數組中的所有元素arr.length = 0;for (let i = 0; i < buckets.length; i++) {// 對每個桶進行排序，這里使用了插入排序insertionSort(buckets[i]);// 將每個桶的數據從小到大拿出                    for (let j = 0; j < buckets[i].length; j++) {arr.push(buckets[i][j]);}}return arr;
}
console.log(bucketSort([3, 1, 2, 3134, 113, 342, 123412, 55, 111, 4, 234, 5, 5]))


特點

  1. 時間復雜度：O(N+K)
  2. 空間復雜度：O(N+K)
  3. 穩定性：穩定


基數排序

確定最大數的位數，先按第一位進行排序，在按第二位進行排序，直到按最后一位進行排序為止。


圖解


js實現

function radixSort(arr) {let counter = [];//獲取元素的最大位數let maxDigit = `${Math.max(...arr)}`.lengthlet mod = 10;let dev = 1;//從小到大依次對元素的每一位進行循環排序for (let i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {for (let j = 0; j < arr.length; j++) {//獲取元素對應位上的數值let bucket = parseInt((arr[j] % mod) / dev);if (counter[bucket] == null) {counter[bucket] = [];}//根據對應的數值，將元素放入對應的桶中counter[bucket].push(arr[j]);}let pos = 0;//從0~9的桶中將元素取出，完成一次排序for (let j = 0; j < counter.length; j++) {let value = null;if (counter[j] != null) {while ((value = counter[j].shift()) != null) {arr[pos++] = value;}}}}return arr;
}
console.log(radixSort([3, 1, 2, 3134, 113, 342, 123412, 55, 111, 4, 234, 5, 5], 6))


特點

  1. 時間復雜度：O(N*K)
  2. 空間復雜度：O(N+K)
  3. 穩定性：穩定


歸并排序

  1. 申請空間，使其大小為兩個已經排序序列之和，該空間用來存放合并后的序列；

  2. 設定兩個指針，最初位置分別為兩個已經排序序列的起始位置；

  3. 比較兩個指針所指向的元素，選擇相對小的元素放入到合并空間，并移動指針到下一位置；

  4. 重復步驟 3 直到某一指針達到序列尾；

  5. 將另一序列剩下的所有元素直接復制到合并序列尾。


圖解


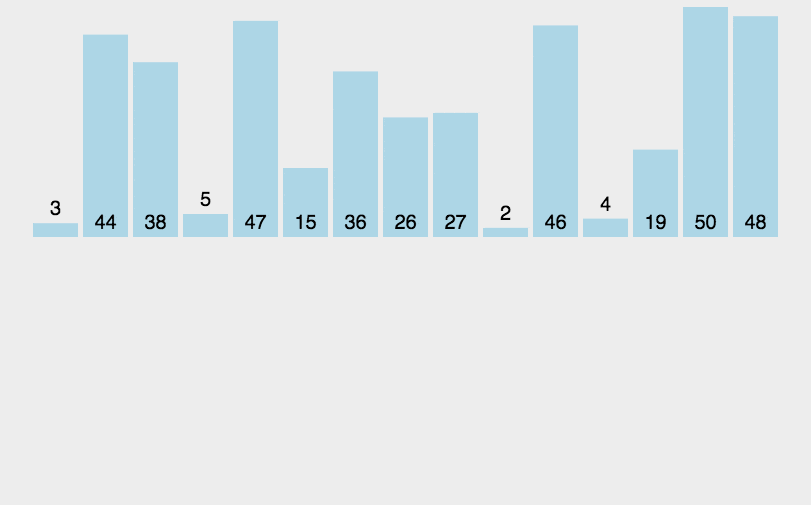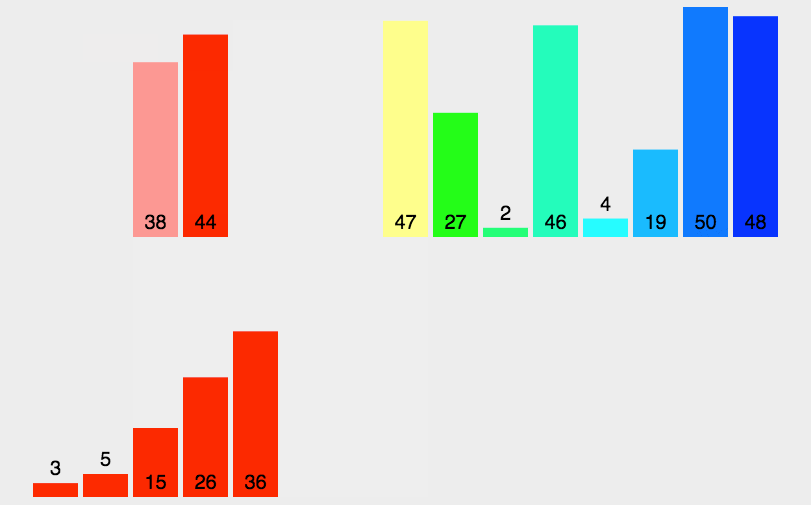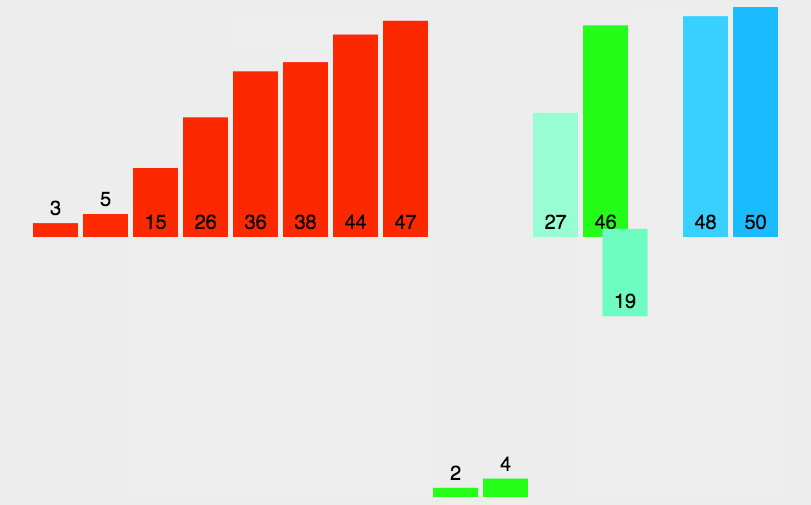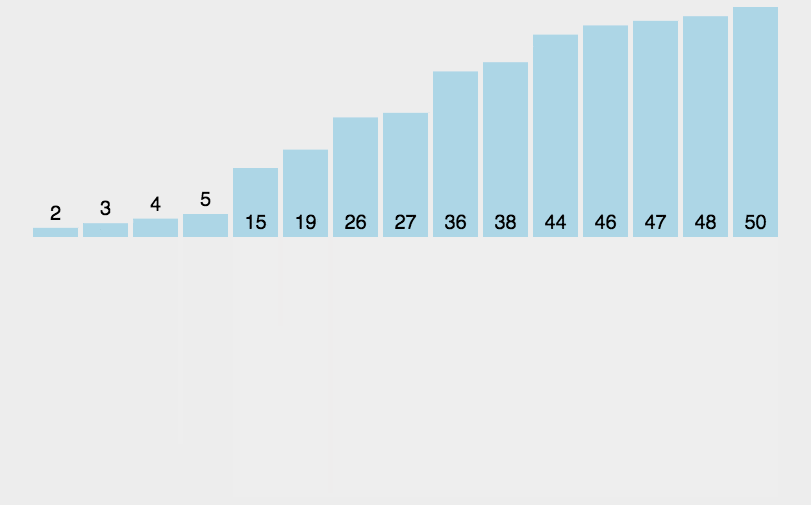
?js實現

function mergeSort(arr) {  // 采用自上而下的遞歸方法let len = arr.length;if (len < 2) {return arr;}let middle = Math.floor(len / 2),left = arr.slice(0, middle),right = arr.slice(middle);return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {let result = [];while (left.length && right.length) {if (left[0] <= right[0]) {result.push(left.shift());} else {result.push(right.shift());}}while (left.length)result.push(left.shift());while (right.length)result.push(right.shift());return result;
}
console.log(mergeSort([3, 1, 2, 3134, 113, 342, 123412, 55, 111, 4, 234, 5, 5], 6))


特點

  1. 時間復雜度：O(N*logN)
  2. 空間復雜度：O(N)
  3. 穩定性：穩定


計數排序

1.找出待排序的數組中最大和最小的元素

2.統計數組中每個值為i的元素出現的次數，存入數組C的第i項

3.對所有的計數累加（從C中的第一個元素開始，每一項和前一項相加）

4.反向填充目標數組：將每個元素i放在新數組的第C(i)項，每放一個元素就將C(i)減去1


圖解


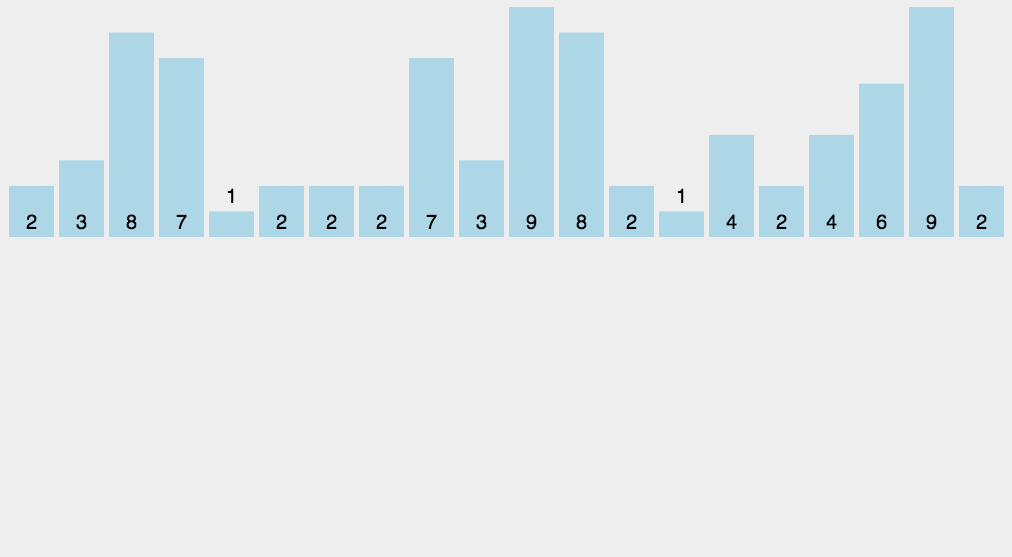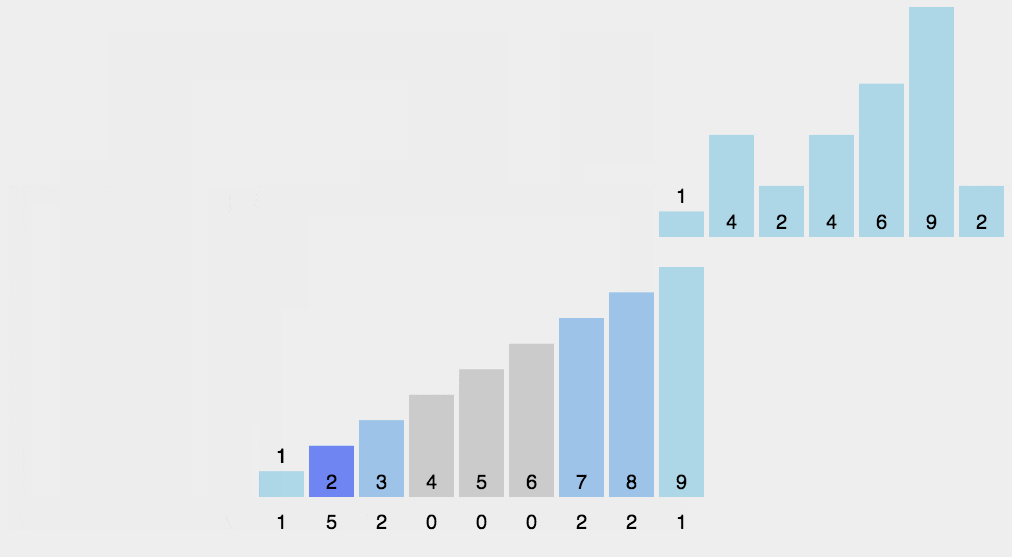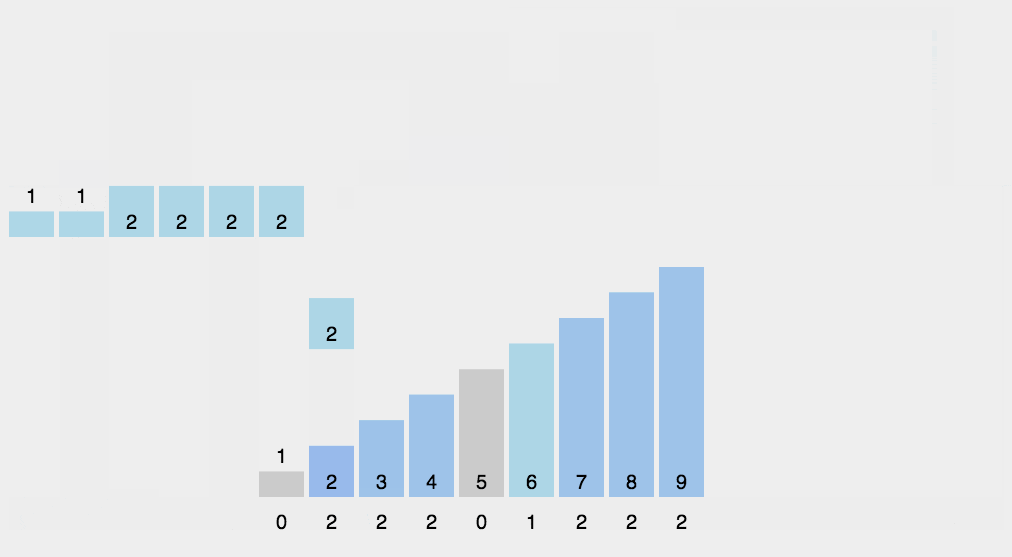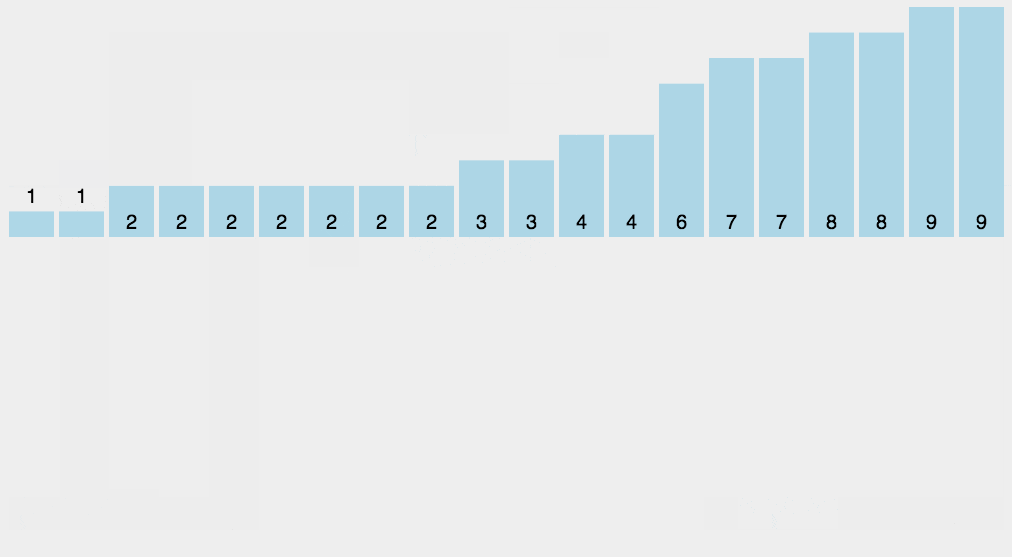
?js實現

function countingSort(arr) {let maxValue = Math.max(...arr)let bucket = new Array(maxValue + 1),sortedIndex = 0;arrLen = arr.length,bucketLen = maxValue + 1;for (let i = 0; i < arrLen; i++) {if (!bucket[arr[i]]) {bucket[arr[i]] = 0;}bucket[arr[i]]++;}for (let j = 0; j < bucketLen; j++) {while (bucket[j] > 0) {arr[sortedIndex++] = j;bucket[j]--;}}return arr;
}
console.log(countingSort([3, 1, 2, 3134, 113, 342, 123412, 55, 111, 4, 234, 5, 5]))


特點

  1. 時間復雜度：O(N+K)
  2. 空間復雜度：O(K)
  3. 穩定性：穩定


---------------------
作者：YF-SOD
來源：CSDN
原文：https://blog.csdn.net/AIWWY/article/details/121346132
版權聲明：本文為作者原創文章，轉載請附上博文鏈接！
內容解析By：CSDN,CNBLOG博客文章一鍵轉載插件

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/284535.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/284535.shtml
英文地址，請注明出處：http://en.pswp.cn/news/284535.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

三維重建技術概述

三維重建技術概述

基于視覺的三維重建&#xff0c;指的是通過攝像機獲取場景物體的數據圖像&#xff0c;并對此圖像進行分析處理&#xff0c;再結合計算機視覺知識推導出現實環境中物體的三維信息。 1. 相關概念 &#xff08;1&#xff09;彩色圖像與深度圖像 彩色圖像也叫作RGB圖像&#xff0c;…
閱讀更多...
【ArcGIS微課1000例】0032：ArcGIS中河流（曲線）、湖泊（水體色）圖例制作案例教程

【ArcGIS微課1000例】0032：ArcGIS中河流（曲線）、湖泊（水體色）圖例制作案例教程

河流作為線要素，在符號化的過程中使用的大多都是直線符號，但是為了能夠在出圖的使用表現形象的河流對象，就有了使用曲線表示河流圖例的需求，湖泊亦是如此。本文講解在ArcGIS中制作標準的河流和湖泊圖例的完整教程。 文章目錄 一、案例效果二、圖例制作三、圖例修改一、案例…
閱讀更多...
從shiro源碼角度學習工廠方法設計模式

從shiro源碼角度學習工廠方法設計模式

緒論 shiro是一個簡單易用&#xff0c;功能強大的Java安全框架&#xff0c;學習其源碼設計思想對我們的編碼水平的提高大有裨益。現在&#xff0c;就從源碼角度帶大家學習一下shiro里面的工廠方法模式。 這里的前提是讀者有過使用shiro的基礎&#xff0c;沒有也行&#xff0c;關…
閱讀更多...
淺談微信小程序對于房地產行業的影響

淺談微信小程序對于房地產行業的影響

前幾日&#xff0c;我們曾經整理過一篇文章是關于微信小程序對于在線旅游業的影響的一些反思&#xff08;淺談微信小程序對OTA在線旅游市場的影響&#xff09;&#xff0c;近日由于生活工作的需要走訪了一些房地產的住宅商品房&#xff0c;突然想到微信小程序對于房地產行業會有…
閱讀更多...
新型基礎測繪與實景三維中國建設技術文件【1】名詞解釋

新型基礎測繪與實景三維中國建設技術文件【1】名詞解釋

文章目錄一、新型基礎測繪 new fundamental surveying and mapping**二、實景三維 3D real scene**三、時空大數據平臺 spatio-temporal big data platform**四、地理實體 geo-entity**五、基礎地理實體 fundamental geo-entity**六、組合地理實體數據 combined geo-entity dat…
閱讀更多...
Android.bp 和 Android.mk 的對應關系

Android.bp 和 Android.mk 的對應關系

參考 Soong 構建系統 Android.mk 轉為 Android.bp 沒有分支、循環等流程控制的簡單的 Android.mk &#xff0c;可以通過 androidmk 命令轉化為 Android.bp source 、lunch 之后執行即可。 androidmk Android.mk > Android.bp對應關系 Android 13 &#xff0c;build/soon…
閱讀更多...
深入理解javascript原型和閉包

深入理解javascript原型和閉包

原文鏈接http://www.cnblogs.com/wangfupeng1988/p/3977924.html 對象是屬性的集合。 function show(x) {console.log(typeof(x)); // undefinedconsole.log(typeof(10)); // numberconsole.log(typeof(abc)); // stringconsole.log(typeof(true)); // booleanconsole.lo…
閱讀更多...
薪資高壓線

薪資高壓線

閱讀本文大概需要5分鐘。最近一名讀者咨詢一個問題&#xff1a;洋哥&#xff0c;最近公司有一名同事因為打探其他人薪資被開除了&#xff0c;為啥我們公司要把薪資設置為高壓線。這是個好問題&#xff0c;解答完他的疑惑后想起了一年多前寫過一篇&#xff0c;彼時讀者還比較少&…
閱讀更多...
達摩院年終預測出爐：2022 十大科技趨勢，AI for Science 高居榜首

達摩院年終預測出爐：2022 十大科技趨勢，AI for Science 高居榜首

作為“一所探索科技未知的研究院”&#xff0c;阿里巴巴達摩院成立至今已經四年了。 這四年來&#xff0c;達摩院秉持著“探索科技位置&#xff0c;以人類愿景為驅動力&#xff0c;開展基礎科學和顛覆式技術創新研究”的原則與使命&#xff0c;在基礎科研和硬科技發展上“遍地生…
閱讀更多...
chrome調試工具高級不完整使用指南（基礎篇）

chrome調試工具高級不完整使用指南（基礎篇）

一、前言 本文記錄的是作者在工作上面對chrome的一些使用和情況的分析分享&#xff0c;內容僅代表個人的觀點。轉發請注明出處(http://www.cnblogs.com/st-leslie/),謝謝合作 二、瀏覽器模塊介紹 由于chrome瀏覽器一直在不斷的進行更新迭代&#xff0c;會不斷的新增功能&#x…
閱讀更多...
新型基礎測繪與實景三維中國建設技術文件【2】基礎地理實體分類、粒度及精度基本要求

新型基礎測繪與實景三維中國建設技術文件【2】基礎地理實體分類、粒度及精度基本要求

《新型基礎測繪體系建設試點技術大綱》指出&#xff0c;新型基礎測繪將以“基礎地理實體”為核心的成果模式創新為切入點&#xff0c;帶動技術體系、生產組織體系和政策標準體系的全面創新&#xff0c;從而實現基礎測繪高質量發展。 基礎地理實體作為新型基礎測繪產品體系的核心…
閱讀更多...
構建和實現單點登錄解決方案（轉載于IBMdeveloperWorks）

構建和實現單點登錄解決方案（轉載于IBMdeveloperWorks）

將一個開放源碼的基于 Java 的身份驗證組件集成進 Web 門戶中 在現有的應用程序中實現單點登錄解決方案&#xff08;single sign-on&#xff0c;SSO&#xff0c;即登錄一次&#xff0c;就可以向所有網絡資源驗證用戶的身份&#xff09;是非常困難的&#xff0c;但是在構建復雜的…
閱讀更多...
分享一個基于Abp 和Yarp 開發的API網關項目

分享一個基于Abp 和Yarp 開發的API網關項目

這個項目起源于去年公司相要嘗試用微服務構建項目,在網關的技術選型中,我們原本確認了ApiSix 網關,如果需要寫網關插件需要基于Lua腳本去寫,我和另外一個同事當時基于這個寫了一個簡單的插件,但是開發測試以及發布都很麻煩,而且使用Lua腳本作為插件的開發語言本身也不是我們強項…
閱讀更多...
羅振宇2022“時間的朋友”跨年演講全文稿（pdf）

羅振宇2022“時間的朋友”跨年演講全文稿（pdf）

2021年12月31日20:30&#xff0c;五糧液成都金融城演藝中心&#xff0c;羅振宇“時間的朋友”跨年演講如約而至。 羅胖曾發下大愿望&#xff1a;跨年演講要連辦二十年。今年是第七場&#xff0c;也是最特殊的一場&#xff0c;羅胖面對12000個空座位&#xff0c;用53個好故事&am…
閱讀更多...
08.LoT.UI 前后臺通用框架分解系列之——多樣的Tag選擇器

08.LoT.UI 前后臺通用框架分解系列之——多樣的Tag選擇器

LOT.UI分解系列匯總&#xff1a;http://www.cnblogs.com/dunitian/p/4822808.html#lotui LoT.UI開源地址如下&#xff1a;https://github.com/dunitian/LoTCodeBase/tree/master/LoTUI 這個必須說下&#xff0c;本來是用Bootstrap-Select做的&#xff0c;很漂亮&#xff0c;正好…
閱讀更多...
jquery文檔加載完畢后執行的幾種寫法

jquery文檔加載完畢后執行的幾種寫法

2019獨角獸企業重金招聘Python工程師標準>>> 1.js文檔加載完畢 標簽內 οnlοad"test()"window.οnlοadfunction(){}2.jquery文檔加載完畢 //方式1 $(document).ready(function(){//TODO }); //方式2 $(function(){//TODO }) //方式3 $(function($){//TO…
閱讀更多...
新型基礎測繪與實景三維中國建設技術文件【3】基礎地理實體空間身份編碼規則

新型基礎測繪與實景三維中國建設技術文件【3】基礎地理實體空間身份編碼規則

基礎地理實體是新型基礎測繪產品體系中的核心成果&#xff0c;是推動基礎測繪工作轉型升級的關鍵。與現有的測繪地理信息數據不同&#xff0c;基礎地理實體具有多粒度、多模態、多層次&#xff0c;以及搭載結構化、半結構化和非結構化多樣化信息的鮮明特點。 基礎地理實體空間…
閱讀更多...
oracle 表 視圖 存儲過程 序列 job

oracle 表 視圖 存儲過程 序列 job

table 表--delete tabledrop table Test1;-- Create tablecreate table TEST1(ID NUMBER,T_NAME VARCHAR2(100),DT DATE);-- 添加注釋comment on column TEST1.T_NAME is 名稱;--添加age字段alter table Test1 add (age NUMBER(8));--刪除字段alter table TABLE_NAME …
閱讀更多...
[轉]Docker 大勢已去，Podman 即將崛起

[轉]Docker 大勢已去，Podman 即將崛起

Podman Podman 什么是Podman&#xff1f;Podman和Docker的主要區別是什么&#xff1f;Podman的使用與docker有什么區別&#xff1f;Podman 常用命令 容器鏡像部署 PodmanPodman 加速器使用 Podman 運行一個容器列出運行的容器檢查正在運行的容器查看一個運行中容器的日志查看一…
閱讀更多...
基于Kubernetes v1.24.0的集群搭建（一）

基于Kubernetes v1.24.0的集群搭建（一）

一、寫在前面 K8S 1.24作為一個很重要的版本更新&#xff0c;它為我們提供了很多重要功能。該版本涉及46項增強功能&#xff1a;其中14項已升級為穩定版&#xff0c;15項進入beta階段&#xff0c;13項則剛剛進入alpha階段。此外&#xff0c;另有2項功能被棄用、2項功能被刪除。…
閱讀更多...
最新文章

Copyright @ 2022~2023