?一、樹
1、什么是樹?
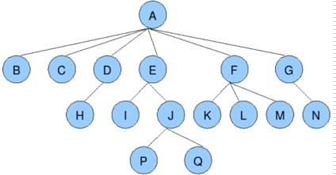
- 節點的度:一個節點含有的子樹的個數稱為該節點的度;
- 葉節點或終端節點:度為0的節點稱為葉節點;
- 非終端節點或分支節點:度不為0的節點;
- 雙親節點或父節點:若一個節點含有子節點,則這個節點稱為其子節點的父節點;
- 孩子節點或子節點:一個節點含有的子樹的根節點稱為該節點的子節點;
- 兄弟節點:具有相同父節點的節點互稱為兄弟節點;
- 樹的度:一棵樹中,最大的節點的度稱為樹的度;
- 節點的層次:從根開始定義起,根為第1層,根的子節點為第2層,以此類推;
- 樹的高度或深度:樹中節點的最大層次;
- 堂兄弟節點:雙親在同一層的節點互為堂兄弟;
- 節點的祖先:從根到該節點所經分支上的所有節點;
- 子孫:以某節點為根的子樹中任一節點都稱為該節點的子孫。
- 森林:由m(m>=0)棵互不相交的樹的集合稱為森林;
二、二叉樹
1、什么是二叉樹?
二叉樹,就是度不差過2的樹(節點最多有兩個叉)
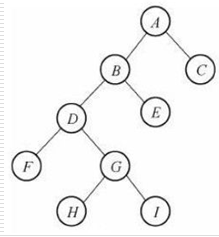
三、兩種特殊的二叉樹
1、滿二叉樹
一個二叉樹,如果每一個層的結點數都達到最大值,則這個二叉樹就是滿二叉樹。
2、完全二叉樹
葉節點只能出現在最下層和次下層,并且最下面一層的結點都集中在該層最左邊的若干位置的二叉樹
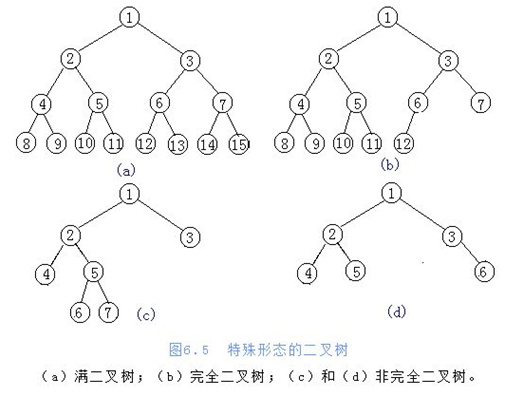
滿二叉樹一定是完全二叉樹,但是完全二叉樹不一定是滿二叉樹
三、二叉樹的存儲方式
1、鏈式存儲方式
a、二叉樹的鏈式存儲:將二叉樹的節點定義為一個對象,節點之間通過類似鏈表的鏈接方式來連接。
b、節點定義
class BiTreeNode:def __init__(self,data): #data就是傳進去的節點的值self.data = dataself.lchild = Noneself.rchild = None
?
c、二叉樹的遍歷:
I 、先(前)序遍歷:訪問根結點的操作發生在遍歷其左右子樹之前
- ⑴ 訪問根結點;
- ⑵ 遍歷左子樹;
- ⑶ 遍歷右子樹。
II、中序遍歷:訪問根結點的操作發生在遍歷其左右子樹之中(間)。
- ⑴遍歷左子樹;
- ⑵訪問根結點;
- ⑶遍歷右子樹。
III、后序遍歷:訪問根結點的操作發生在遍歷其左右子樹之后。
- ⑴遍歷左子樹;
- ⑵遍歷右子樹;
- ⑶訪問根結點。
IV、層次遍歷
用一個隊列保存被訪問的當前節點的左右孩子以實現層序遍歷。
二叉樹的遍歷代碼如下
from collections import deque #雙向隊列 from queue import Queue #單向隊列# import queue # q = queue.Queue() # q.put('ggg') # q.get() class BiTreeNode:def __init__(self,data):self.data = dataself.lchild = Noneself.rchild = None@classmethoddef pre_order(self,root):'''前序遍歷(根左右)'''if root: #如果有根節點print(root.data,end='')self.pre_order(root.lchild)self.pre_order(root.rchild)@classmethoddef in_order(self,root):'''中序遍歷(左根右)'''if root:self.in_order(root.lchild)print(root.data,end='')self.in_order(root.rchild)@classmethoddef out_order(self, root):'''后序遍歷(左右根)'''if root:self.out_order(root.lchild)self.out_order(root.rchild)print(root.data, end='')@classmethoddef level_order(self,root):'''層次遍歷(第一層,第二層,第三層...借助隊列來實現)'''queue = deque()queue.append(root)while len(queue) > 0:node = queue.popleft()print(node.data,end='')if node.lchild:queue.append(node.lchild)if node.rchild:queue.append(node.rchild)#創建二叉樹 a = BiTreeNode("A") b = BiTreeNode("B") c = BiTreeNode("C") d = BiTreeNode("D") e = BiTreeNode("E") f = BiTreeNode("F") g = BiTreeNode("G") e.lchild = a e.rchild = g a.rchild = c c.lchild = b c.rchild = d g.rchild = f root = e#查看前序遍歷的結果 BiTreeNode.pre_order(root) #EACBDGF print('') BiTreeNode.in_order(root) #ABCDEGF print('') BiTreeNode.out_order(root) #BDCAFGE print('') BiTreeNode.level_order(root) #EAGCFBD
?
2、順序存儲方式
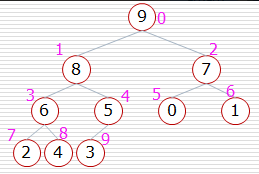
如上圖二叉樹標出了元素所對應的索引,那么可以有一下結論
1、父節點和左孩子節點的編號下標有什么關系?
如果已知父親節點為i,那么他的左孩子節點為2i+1
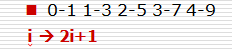
2、父節點和右孩子節點的編號下標有什么關系?

3、反過來知道孩子找父親
(n-1)/2=i # 左孩子求父節點 (n-2)/2=i # 右孩子求父節點
?四、二叉搜索樹
1、定義
二叉搜索樹是一棵二叉樹且滿足性質:設X是二叉樹的一個節點。如果Y是X左子樹的一個節點,那么Y.key <=X.key;
如果Y是X右子樹的一個節點,那么Y.key>= X.key? (X.key代表X節點對應的值)
通俗的說也就是?若它的左子樹不空,則左子樹上所有結點的值均小于它的根結點的值; 若它的右子樹不空,則右子樹上所有結點的值均大于它的根結點的值; 它的左、右子樹也分別為二叉搜索樹。
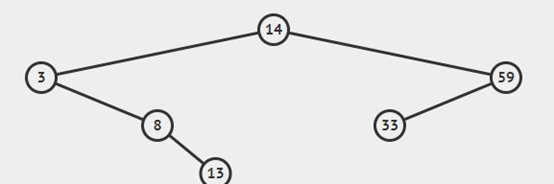
2、原理
二叉排序樹的查找過程和次優二叉樹類似,通常采取二叉鏈表作為二叉排序樹的存儲結構。中序遍歷二叉排序樹可得到一個關鍵字的有序序列,一個無序序列可以通過構造一棵二叉排序樹變成一個有序序列,構造樹的過程即為對無序序列進行排序的過程。每次插入的新的結點都是二叉排序樹上新的葉子結點,在進行插入操作時,不必移動其它結點,只需改動某個結點的指針,由空變為非空即可。搜索,插入,刪除的復雜度等于樹高,O(log(n)).
3、二叉搜索樹的創建
可參考鏈接:https://visualgo.net/en/bst
4、二叉搜索樹的遍歷
5、二叉搜索樹的查詢、插入、刪除
插入:
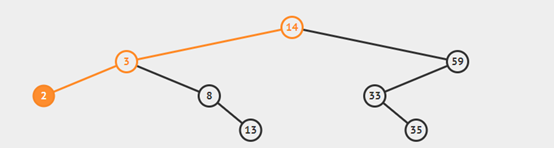
刪除
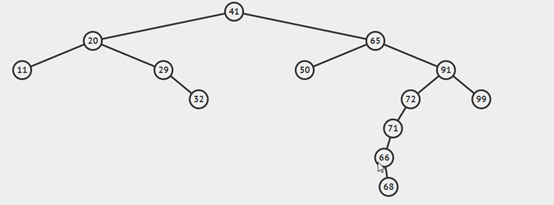
比如要刪除65
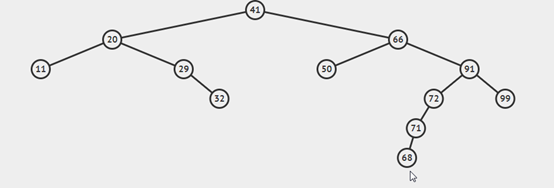
比如要刪除66
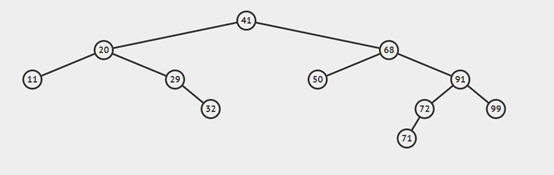
代碼實現:
?待續....
6、二叉搜索樹存在的問題
存在的問題:當插入的是有序的時候,假如插入的數據特別多,找是能找到,但是是很花費時間的。
可以有以下解決辦法:
1、隨機化的二叉搜索樹(打亂順序插入)
? 2、AVL樹
查找方法有:二分查找、二叉搜索樹、哈希查找、順序查找、斐波那契查找
五、AVL樹-----擴展(了解)
1、AVL樹:AVL樹是一棵自平衡的二叉搜索樹
2、AVL樹具有以下性質:
- 根的左右子樹的高度只差的絕對值不能超過1
- 根的左右子樹都是平衡二叉樹
3、AVL的實現方式:旋轉
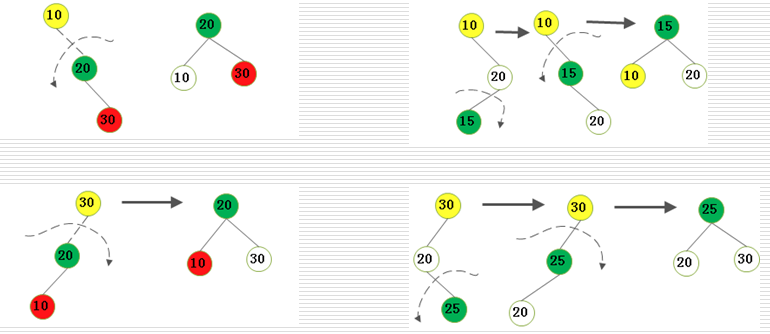
?
六、B樹
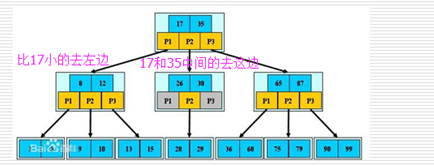
1、B樹:B樹是一棵自平衡的多路搜索樹。常用于數據庫的索引
?
七、其他
?







)











