?
????
- 1. 順序查找
- 2. 二分查找
- 3. 插值查找
- 4. 斐波那契查找
- 5. 樹表查找
- 6. 分塊查找
- 7. 哈希查找
查找是在大量的信息中尋找一個特定的信息元素,在計算機應用中,查找是常用的基本運算,例如編譯程序中符號表的查找。本文簡單概括性的介紹了常見的七種查找算法,說是七種,其實二分查找、插值查找以及斐波那契查找都可以歸為一類——插值查找。插值查找和斐波那契查找是在二分查找的基礎上的優化查找算法。樹表查找和哈希查找會在后續的博文中進行詳細介紹。
????查找定義:根據給定的某個值,在查找表中確定一個其關鍵字等于給定值的數據元素(或記錄)。
查找算法分類:
? ? ?1)靜態查找和動態查找;
注:靜態或者動態都是針對查找表而言的。動態表指查找表中有刪除和插入操作的表。
2)無序查找和有序查找。
無序查找:被查找數列有序無序均可;
有序查找:被查找數列必須為有序數列。
?
平均查找長度(Average Search Length,ASL):需和指定key進行比較的關鍵字的個數的期望值,稱為查找算法在查找成功時的平均查找長度。
對于含有n個數據元素的查找表,查找成功的平均查找長度為:ASL = Pi*Ci的和。
Pi:查找表中第i個數據元素的概率。
Ci:找到第i個數據元素時已經比較過的次數。
1. 順序查找
????????說明:順序查找適合于存儲結構為順序存儲或鏈接存儲的線性表。
基本思想:順序查找也稱為線形查找,屬于無序查找算法。從數據結構線形表的一端開始,順序掃描,依次將掃描到的結點關鍵字與給定值k相比較,若相等則表示查找成功;若掃描結束仍沒有找到關鍵字等于k的結點,表示查找失敗。
復雜度分析:
查找成功時的平均查找長度為:(假設每個數據元素的概率相等) ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;
當查找不成功時,需要n+1次比較,時間復雜度為O(n);
所以,順序查找的時間復雜度為O(n)。
C++實現源碼:
//順序查找
int SequenceSearch(int a[], int value, int n)
{int i;for(i=0; i<n; i++)if(a[i]==value)return i;return -1;
}? java實現源碼:
?
?
public class sequence{public static? boolean SequenceSearch(int a[],int k,int value){for( int i = 0 ; i<k;i++){if( value == a[i])return true;elsereturn false;}return false;}public static void main(String[] args) {int[] a = {8,2,4,5,3,10,11,6,9};System.out.println(SequenceSearch(a,a.length,20));}
}
//printf: false
public static? boolean SequenceSearch(int a[],int k,int value){for( int i = 0 ; i<k;i++){if( value == a[i])return true;elsereturn false;}return false;}public static void main(String[] args) {int[] a = {8,2,4,5,3,10,11,6,9};System.out.println(SequenceSearch(a,a.length,20));}
}
//printf: false
?
?
2. 二分查找
說明:元素必須是有序的,如果是無序的則要先進行排序操作。
基本思想:也稱為是折半查找,屬于有序查找算法。用給定值k先與中間結點的關鍵字比較,中間結點把線形表分成兩個子表,若相等則查找成功;若不相等,再根據k與該中間結點關鍵字的比較結果確定下一步查找哪個子表,這樣遞歸進行,直到查找到或查找結束發現表中沒有這樣的結點。
復雜度分析:最壞情況下,關鍵詞比較次數為log2(n+1),且期望時間復雜度為O(log2n);
注:折半查找的前提條件是需要有序表順序存儲,對于靜態查找表,一次排序后不再變化,折半查找能得到不錯的效率。但對于需要頻繁執行插入或刪除操作的數據集來說,維護有序的排序會帶來不小的工作量,那就不建議使用。——《大話數據結構》
C++實現源碼:
//二分查找(折半查找),版本1
int BinarySearch1(int a[], int value, int n)
{int low, high, mid;low = 0;high = n-1;while(low<=high){mid = (low+high)/2;if(a[mid]==value)return mid;if(a[mid]>value)high = mid-1;if(a[mid]<value)low = mid+1;}return -1;
}//二分查找,遞歸版本
int BinarySearch2(int a[], int value, int low, int high)
{int mid = low+(high-low)/2;if(a[mid]==value)return mid;if(a[mid]>value)return BinarySearch2(a, value, low, mid-1);if(a[mid]<value)return BinarySearch2(a, value, mid+1, high);
}java 實現源碼:
/*1.*/
public class BinarySearch1{public static int binarysearch(int[] a,int n,int value){int low = 0;int high = n - 1;int mid;while(low < high){mid = (low + high)/2;if(value < a[mid])high = mid - 1;if(value > a[mid])low = mid + 1;if(value == a[mid])return mid;}return -1;}public static void main(String[] args) {//int[] a = {1,4,2,9,8,6,7,0,3,5}int[] a = {0,1,2,3,4,5,6,7,8,9};System.out.println(binarysearch(a,a.length,7));}?
} public static int binarysearch(int[] a,int n,int value){int low = 0;int high = n - 1;int mid;while(low < high){mid = (low + high)/2;if(value < a[mid])high = mid - 1;if(value > a[mid])low = mid + 1;if(value == a[mid])return mid;}return -1;}public static void main(String[] args) {//int[] a = {1,4,2,9,8,6,7,0,3,5}int[] a = {0,1,2,3,4,5,6,7,8,9};System.out.println(binarysearch(a,a.length,7));}?
}/*2.recursive algorithm */
public class BinarySearch2{public static int binarysearch(int[] a,int value,int low,int high){int mid = (low + high)/2;if(value == a[mid])return mid;mid = (low + high)/2;if(value < a[mid])return binarysearch(a,value,low,mid - 1);if(value > a[mid])return binarysearch(a,value,mid + 1,high); return -1;}public static void main(String[] args) {//int[] a = {1,4,2,9,8,6,7,0,3,5}int[] a = {0,1,2,3,4,5,6,7,8,9};System.out.println(binarysearch(a,4,0,a.length-1));}
}3. 插值查找
在介紹插值查找之前,首先考慮一個新問題,為什么上述算法一定要是折半,而不是折四分之一或者折更多呢?
打個比方,在英文字典里面查“apple”,你下意識翻開字典是翻前面的書頁還是后面的書頁呢?如果再讓你查“zoo”,你又怎么查?很顯然,這里你絕對不會是從中間開始查起,而是有一定目的的往前或往后翻。
同樣的,比如要在取值范圍1 ~ 10000 之間 100 個元素從小到大均勻分布的數組中查找5, 我們自然會考慮從數組下標較小的開始查找。
經過以上分析,折半查找這種查找方式,不是自適應的(也就是說是傻瓜式的)。二分查找中查找點計算如下:
mid=(low+high)/2, 即mid=low+1/2*(high-low);
通過類比,我們可以將查找的點改進為如下:
mid=low+(key-a[low])/(a[high]-a[low])*(high-low),
也就是將上述的比例參數1/2改進為自適應的,根據關鍵字在整個有序表中所處的位置,讓mid值的變化更靠近關鍵字key,這樣也就間接地減少了比較次數。
基本思想:基于二分查找算法,將查找點的選擇改進為自適應選擇,可以提高查找效率。當然,差值查找也屬于有序查找。
注:對于表長較大,而關鍵字分布又比較均勻的查找表來說,插值查找算法的平均性能比折半查找要好的多。反之,數組中如果分布非常不均勻,那么插值查找未必是很合適的選擇。
復雜度分析:查找成功或者失敗的時間復雜度均為O(log2(log2n))。
java代碼實現:
public class InsertionSearch{public static int InsertionSearch(int[] a, int value, int low, int high){int mid = low+(value-a[low])/(a[high]-a[low])*(high-low);if(a[mid]==value)return mid; if(a[mid]>value)return InsertionSearch(a, value, low, mid-1);if(a[mid]<value)return InsertionSearch(a, value, mid+1, high);return -1;}public static void main(String[] args) {int[] a = {0,1,2,3,4,5,6,7,8,9};System.out.println(InsertionSearch(a,2,0,a.length-1));}
}?
4. 斐波那契查找
在介紹斐波那契查找算法之前,我們先介紹一下很它緊密相連并且大家都熟知的一個概念——黃金分割。
黃金比例又稱黃金分割,是指事物各部分間一定的數學比例關系,即將整體一分為二,較大部分與較小部分之比等于整體與較大部分之比,其比值約為1:0.618或1.618:1。
0.618被公認為最具有審美意義的比例數字,這個數值的作用不僅僅體現在諸如繪畫、雕塑、音樂、建筑等藝術領域,而且在管理、工程設計等方面也有著不可忽視的作用。因此被稱為黃金分割。
大家記不記得斐波那契數列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….(從第三個數開始,后邊每一個數都是前兩個數的和)。然后我們會發現,隨著斐波那契數列的遞增,前后兩個數的比值會越來越接近0.618,利用這個特性,我們就可以將黃金比例運用到查找技術中。
基本思想:也是二分查找的一種提升算法,通過運用黃金比例的概念在數列中選擇查找點進行查找,提高查找效率。同樣地,斐波那契查找也屬于一種有序查找算法。
相對于折半查找,一般將待比較的key值與第mid=(low+high)/2位置的元素比較,比較結果分三種情況:
1)相等,mid位置的元素即為所求
2)>,low=mid+1;
? ? ? ? 3)<,high=mid-1。
斐波那契查找與折半查找很相似,他是根據斐波那契序列的特點對有序表進行分割的。他要求開始表中記錄的個數為某個斐波那契數小1,及n=F(k)-1;
?開始將k值與第F(k-1)位置的記錄進行比較(及mid=low+F(k-1)-1),比較結果也分為三種
1)相等,mid位置的元素即為所求
2)>,low=mid+1,k-=2;
????說明:low=mid+1說明待查找的元素在[mid+1,high]范圍內,k-=2 說明范圍[mid+1,high]內的元素個數為n-(F(k-1))=?Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1個,所以可以遞歸的應用斐波那契查找。
3)<,high=mid-1,k-=1。
????說明:low=mid+1說明待查找的元素在[low,mid-1]范圍內,k-=1 說明范圍[low,mid-1]內的元素個數為F(k-1)-1個,所以可以遞歸 的應用斐波那契查找。
復雜度分析:最壞情況下,時間復雜度為O(log2n),且其期望復雜度也為O(log2n)。
5. 樹表查找
5.1 最簡單的樹表查找算法——二叉樹查找算法。
基本思想:二叉查找樹是先對待查找的數據進行生成樹,確保樹的左分支的值小于右分支的值,然后在就行和每個節點的父節點比較大小,查找最適合的范圍。?這個算法的查找效率很高,但是如果使用這種查找方法要首先創建樹。?
二叉查找樹(BinarySearch Tree,也叫二叉搜索樹,或稱二叉排序樹Binary Sort Tree)或者是一棵空樹,或者是具有下列性質的二叉樹:
1)若任意節點的左子樹不空,則左子樹上所有結點的值均小于它的根結點的值;
2)若任意節點的右子樹不空,則右子樹上所有結點的值均大于它的根結點的值;
3)任意節點的左、右子樹也分別為二叉查找樹。
二叉查找樹性質:對二叉查找樹進行中序遍歷,即可得到有序的數列。
????????不同形態的二叉查找樹如下圖所示:
?
復雜度分析:它和二分查找一樣,插入和查找的時間復雜度均為O(logn),但是在最壞的情況下仍然會有O(n)的時間復雜度。原因在于插入和刪除元素的時候,樹沒有保持平衡(比如,我們查找上圖(b)中的“93”,我們需要進行n次查找操作)。我們追求的是在最壞的情況下仍然有較好的時間復雜度,這就是平衡查找樹設計的初衷。
下圖為二叉樹查找和順序查找以及二分查找性能的對比圖:
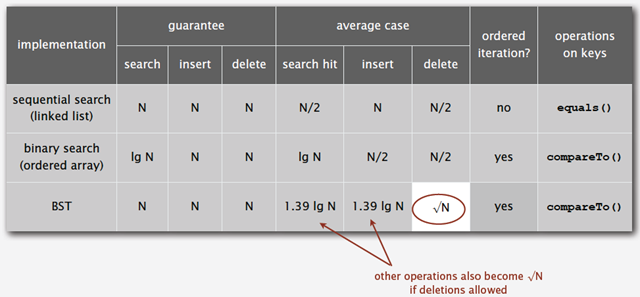
?
基于二叉查找樹進行優化,進而可以得到其他的樹表查找算法,如平衡樹、紅黑樹等高效算法
5.2 平衡查找樹之2-3查找樹(2-3 Tree)
2-3查找樹定義:和二叉樹不一樣,2-3樹運行每個節點保存1個或者兩個的值。對于普通的2節點(2-node),他保存1個key和左右兩個自己點。對應3節點(3-node),保存兩個Key,2-3查找樹的定義如下:
1)要么為空,要么:
2)對于2節點,該節點保存一個key及對應value,以及兩個指向左右節點的節點,左節點也是一個2-3節點,所有的值都比key要小,右節點也是一個2-3節點,所有的值比key要大。
3)對于3節點,該節點保存兩個key及對應value,以及三個指向左中右的節點。左節點也是一個2-3節點,所有的值均比兩個key中的最小的key還要小;中間節點也是一個2-3節點,中間節點的key值在兩個跟節點key值之間;右節點也是一個2-3節點,節點的所有key值比兩個key中的最大的key還要大。
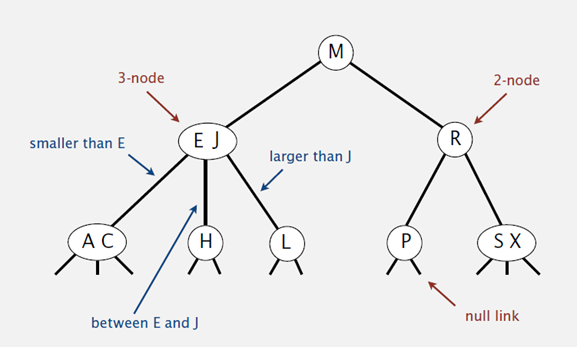
2-3查找樹的性質:
1)如果中序遍歷2-3查找樹,就可以得到排好序的序列;
2)在一個完全平衡的2-3查找樹中,根節點到每一個為空節點的距離都相同。(這也是平衡樹中“平衡”一詞的概念,根節點到葉節點的最長距離對應于查找算法的最壞情況,而平衡樹中根節點到葉節點的距離都一樣,最壞情況也具有對數復雜度。)
性質2)如下圖所示:
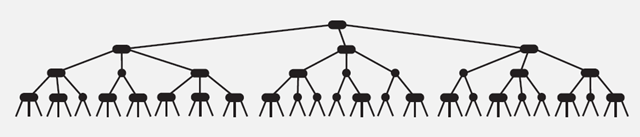
?
復雜度分析:
2-3樹的查找效率與樹的高度是息息相關的。
- 在最壞的情況下,也就是所有的節點都是2-node節點,查找效率為lgN
- 在最好的情況下,所有的節點都是3-node節點,查找效率為log3N約等于0.631lgN
距離來說,對于1百萬個節點的2-3樹,樹的高度為12-20之間,對于10億個節點的2-3樹,樹的高度為18-30之間。
對于插入來說,只需要常數次操作即可完成,因為他只需要修改與該節點關聯的節點即可,不需要檢查其他節點,所以效率和查找類似。下面是2-3查找樹的效率:
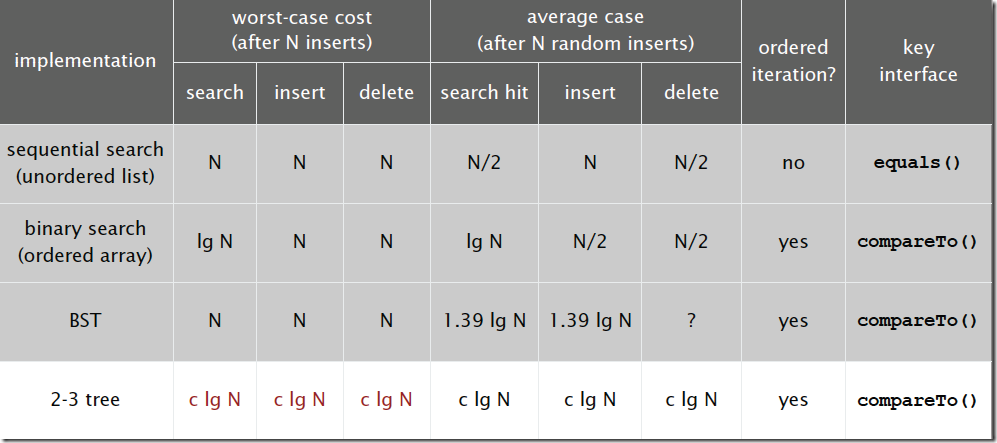
5.3 平衡查找樹之紅黑樹(Red-Black Tree)
2-3查找樹能保證在插入元素之后能保持樹的平衡狀態,最壞情況下即所有的子節點都是2-node,樹的高度為lgn,從而保證了最壞情況下的時間復雜度。但是2-3樹實現起來比較復雜,于是就有了一種簡單實現2-3樹的數據結構,即紅黑樹(Red-Black Tree)。
基本思想:紅黑樹的思想就是對2-3查找樹進行編碼,尤其是對2-3查找樹中的3-nodes節點添加額外的信息。紅黑樹中將節點之間的鏈接分為兩種不同類型,紅色鏈接,他用來鏈接兩個2-nodes節點來表示一個3-nodes節點。黑色鏈接用來鏈接普通的2-3節點。特別的,使用紅色鏈接的兩個2-nodes來表示一個3-nodes節點,并且向左傾斜,即一個2-node是另一個2-node的左子節點。這種做法的好處是查找的時候不用做任何修改,和普通的二叉查找樹相同。
?
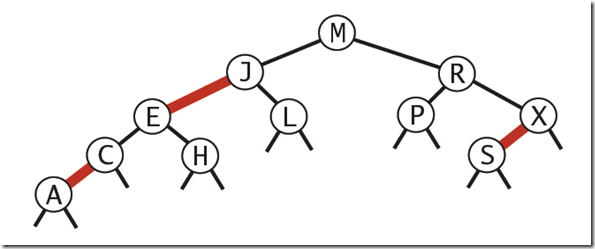
?
紅黑樹的定義:
紅黑樹是一種具有紅色和黑色鏈接的平衡查找樹,同時滿足:
- 紅色節點向左傾斜
- 一個節點不可能有兩個紅色鏈接
- 整個樹完全黑色平衡,即從根節點到所以葉子結點的路徑上,黑色鏈接的個數都相同。
下圖可以看到紅黑樹其實是2-3樹的另外一種表現形式:如果我們將紅色的連線水平繪制,那么他鏈接的兩個2-node節點就是2-3樹中的一個3-node節點了。
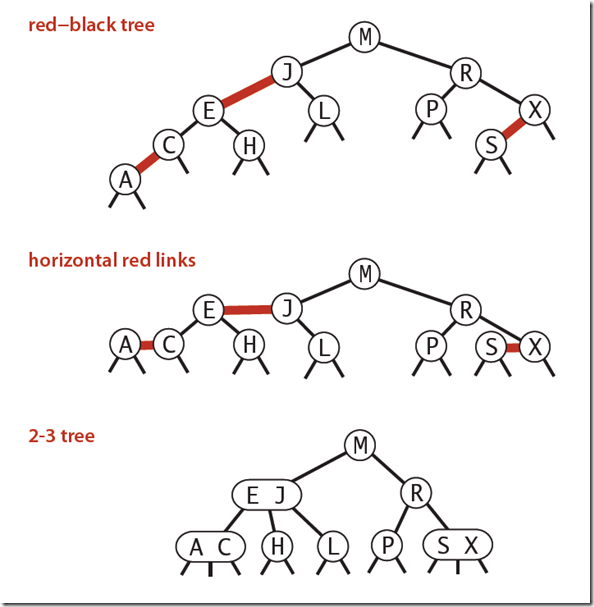
?
紅黑樹的性質:整個樹完全黑色平衡,即從根節點到所以葉子結點的路徑上,黑色鏈接的個數都相同(2-3樹的第2)性質,從根節點到葉子節點的距離都相等)。咋·????
復雜度分析:最壞的情況就是,紅黑樹中除了最左側路徑全部是由3-node節點組成,即紅黑相間的路徑長度是全黑路徑長度的2倍。
下圖是一個典型的紅黑樹,從中可以看到最長的路徑(紅黑相間的路徑)是最短路徑的2倍:
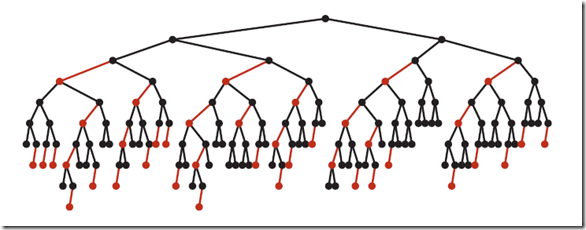
紅黑樹的平均高度大約為logn。
下圖是紅黑樹在各種情況下的時間復雜度,可以看出紅黑樹是2-3查找樹的一種實現,它能保證最壞情況下仍然具有對數的時間復雜度。
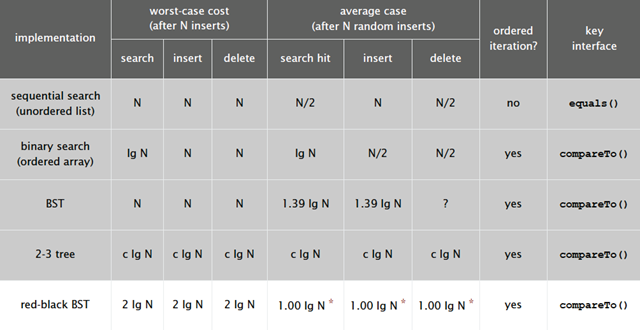
紅黑樹這種數據結構應用十分廣泛,在多種編程語言中被用作符號表的實現,如:
- Java中的java.util.TreeMap,java.util.TreeSet;
- C++ STL中的:map,multimap,multiset;
- .NET中的:SortedDictionary,SortedSet等。
?
?
?
待續....2018/02/26
?
參考文獻:http://www.cnblogs.com/maybe2030/p/4715035.html#_labelTop
?
?














![pb 插入報列在此處不_獲取有關[在此處插入問題]的事實](http://pic.xiahunao.cn/pb 插入報列在此處不_獲取有關[在此處插入問題]的事實)




)

