最近研究3000fps的實現，看了網上給的一個matlab代碼，里面有提到init_shape到mean_shape的對齊，里面使用了fitgeotrans和transformPointsForward兩個函數。于是參考matlab help研究了一下這兩個函數.

fitgeotrans函數

語法:

 tform = fitgeotrans(movingPoints,fixedPoints,transformationType)

說明:

• movingPoints — 圖像上想要移動的點的坐標，至少是兩個double型2維點.
• fixedPoints — 目標點，和上面同等規模
• transformationType — 變換類型，包括如下幾種：

transformationType	Description
‘Affine’	仿射變換
‘NonreflectiveSimilarity’	非反射相似變換（這個有點不懂哎）
‘Projective’	投影變換
‘Similarity’	相似變換（即仿射變換中去除錯切變換）

總結：
這個函數主要描述了將movingPoints（設大小為:N*2,N>=2）通過某種變換變化到fixedPoints來，最后輸出了變換矩陣。tform 是一個結構體類型，里面包含了變換矩陣.

transformPointsForward函數

語法:

[x,y] = transformPointsForward(tform,u,v)
X = transformPointsForward(tform,U)

說明:
tform為變換矩陣. u,v分別代表你要變換的點的x,y序列。u,v必須維數相同.變換后輸出了對應的x,y。
而第二個函數,U包含了[u,v]，X=[x,y]。
注意:
什么是前置變換呢？
即： X=U*tform

兩個例子

例1

theta = 10;
tform = affine2d([cosd(theta) -sind(theta) 0; sind(theta) cosd(theta) 0; 0 0 1])
[X,Y] = transformPointsForward(tform,5,10)

結果:
tform =

affine2d with properties:

             T: [3x3 double]
Dimensionality: 2

其中

而X=6.6605 ， Y=8.9798 。
具體計算方法是:

$$\begin{bmatrix} 6.6605&8.9798&1 \end{bmatrix}=\begin{bmatrix} 5 & 10 & 1 \end{bmatrix}\cdot \begin{bmatrix}0.984807753012208& -0.173648177666930 &0 \\ 0.173648177666930& 0.984807753012208& 0\\ 0& 0 & 1 \end{bmatrix}$$

例2

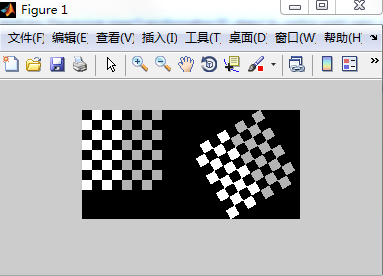
I = checkerboard; %創建棋盤圖
J = imrotate(I,30); %逆時針繞中心旋轉30度
imshowpair(I,J,'montage') %將兩圖并排放在一起

fixedPoints  = [11 11; 41 71];
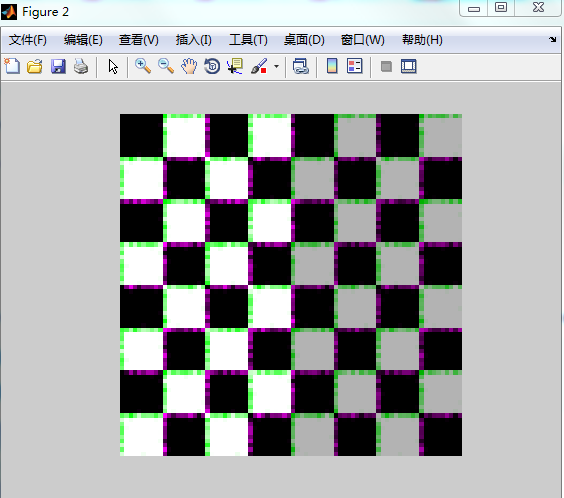
movingPoints = [14 44; 70 81];

tform = fitgeotrans(movingPoints,fixedPoints,'NonreflectiveSimilarity');

Jregistered = imwarp(J,tform,'OutputView',imref2d(size(I))); %應用變換,將圖像旋轉
falsecolorOverlay = imfuse(I,Jregistered); %圖形融合
figure, imshow(falsecolorOverlay,'InitialMagnification','fit');

參考文獻

基于空間幾何變換的人臉對齊(Matlab內置函數)