注:本文如涉及到代碼,均經過Python 3.7實際運行檢驗,保證其嚴謹性。
本文閱讀時間約為6分鐘。
前面說過,如果兩個數據項被散列映射到同一個槽,需要一個系統化的方法在散列表中保存第二個數據項,這個過程被稱為“解決沖突”。
如果散列函數是完美的,那就不會有散列沖突,但實際情況是,完美散列函數常常并不存在,解決散列沖突成為散列方法中很重要的一部分。
解決散列的一種方法就是,為沖突的數據項再找一個開放的空槽來保存。最簡單的就是從沖突的槽開始往后掃描,直到碰到一個空槽。如果到散列表尾部還未找到,則從首部接著掃描。
這種尋找空槽的技術被稱為“開放定址(open addressing)”。
向后逐個槽尋找的方法則是開放定址技術中的“線性探測(linear probing)”。
線性探測Linear Probing
還是以前面說過的這一組數據來作為示例說明線性探測具體如何操作。 假設有下列數據項:
54, 26, 93, 17, 77, 31通過求余法我們得到了其散列值及對應槽號如下圖Pic-512-1的上半部分所示。
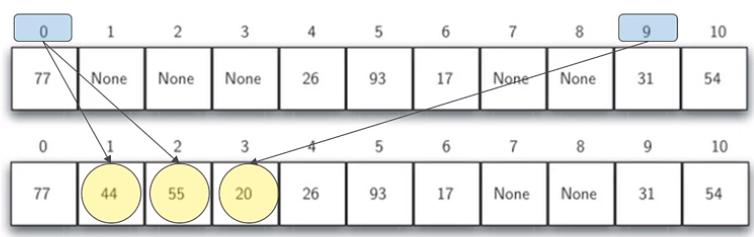
Pic-512-1 線性探測示例
現在,我們要做的是,把44、55、20三個數據項逐個插入到該散列表中。具體過程如下:
h(44)=0,但發現0#槽已被77占據,向后(向右)找到第一個空槽#1,把44保存在1#槽中。
h(55)=0,因為0#槽、1#槽均已被占據,后面的2#槽是空的,因此把55保存在2#槽中。
h(20)=9,發現9#槽已被31占據,向右,10#也被54占據,再從頭掃描,0#、1#、2#等槽均已被占據,后面的3#槽是空的,因此把20保存在3#槽中。
整個過程如上圖Pic-512-1所示。
需要注意的是,如果采用線性探測方法來解決散列沖突的話,那么散列表的查找也應該遵循同樣的規則。
如果在散列位置沒有找到查找項的話,就必須向后做順序查找,直到找到查找項或者碰到空槽(即查找失敗)。
線性探測的改進
線性探測法有一個缺點,就是有聚集的趨勢,即:如果同一個槽沖突的數據項較多的話,這些數據項就會在槽附近聚集起來,從而連鎖式影響其他數據項的插入。
為了避免這種不利的聚集趨勢,一種方法就是將線性探測擴展,從逐個探測改為跳躍式探測。比如,以+3的方式探測插入44、55、20。
還是用線性探測的例子來說明跳躍式探測是具體如何操作的。
還是假設有下列數據項:
54, 26, 93, 17, 77, 31我們現在要把44、55、20三個數據項跳躍式(指定以+3的間隔)插入到該散列表中。具體過程如下:
h(44)=0,但發現0#槽已被77占據,向后+3個槽,找到#3槽。#3槽是空槽,可以存放數據,于是把44保存在3#槽中。
h(55)=0,因為0#槽,向后+3個槽,找到#3槽,已有數據項44;繼續向后+3個槽,找到#6槽,已有數據項17在里面;繼續向后+3個槽,找到#9槽,依然有數據項31占據著;繼續向右+3個槽,到了#1槽。#1槽為空,可以存放數據項,于是把55保存在#1槽中。
h(20)=9,發現9#槽已被31占據,向右+3個槽,找到1#槽,不為空;繼續向右+3個槽,找到#4,有26在里面;繼續向右+3個槽,#7槽為空,可以存放數據項,于是把20存放到#7槽中。
如下圖Pic-512-2所示:
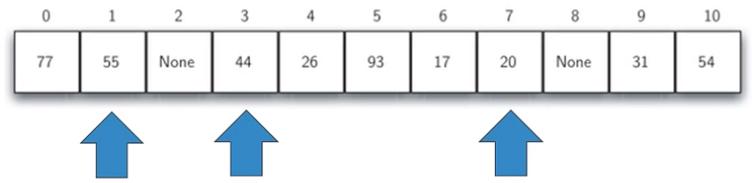
Pic-512-2 跳躍式探測示例
沖突解決方案:再散列rehashing
重新尋找空槽的過程可以用一個更為通用的“再散列rehashing”來概括:
newhashvalue = rehash(oldhashvalue)對于線性探測來說,
rehash(pos) = (pos + 1) % sizeoftable對于“+3”的跳躍式探測則是:
rehash(pos) = (pos + 3) % sizeoftable跳躍式探測的再散列通式是:
rehash(pos) = (pos + skip) % sizeoftable這里要注意的是,skip的取值不能被散列表大小整除,否則會產生周期,造成很多空槽永遠無法探測到的后果。如果把散列表的大小設為質數(如11),則可以避免這種情況。
除了將線性探測改善為跳躍式探測,還能將其變為“二次探測(quadratic probing)”。
二次探測是什么意思呢?就是對于
rehash(pos) = (pos + skip) % sizeoftable來說,skip的值不再是固定的某個值,而是逐步增加的,如1、3、5、7、9等。 這樣槽號就會是原散列值以平方數增加:
h, h+1, h+4, h+9, h+16...這也是一種能令散列值分散的好辦法。
沖突解決方案:數據項鏈Chaining
除了尋找空槽的開放定址技術之外,另一種解決散列沖突的方案是,將容納單個數據項的槽擴展為容納數據項集合(或者對數據項鏈表的引用)。
這樣,散列表中的每個槽就可以容納多個數據項,如果有散列沖突發生,只需要簡單地將數據項添加到數據項集合中。
查找數據項時則需要查找同一個槽中的整個集合。在同一個集合中查找,就用順序查找法。當然,隨著散列沖突的增加,對數據項的查找時間也會相應增加。
還是拿那組數據為例:
54, 26, 93, 17, 77, 31要求插入44、55、20三個數據項。
如用數據項鏈的方法,每個槽都可以容納一個數據項的集合。操作示意如下圖Pic-512-3所示:
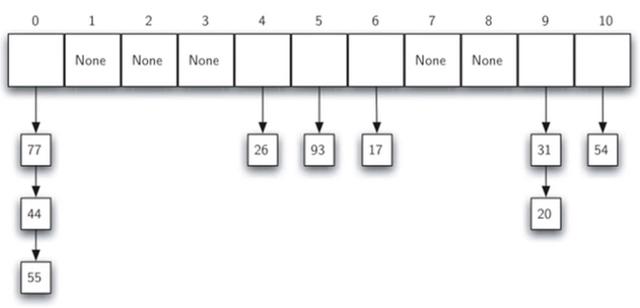
Pic-512-3 數據項鏈示例
To be continued.
)


{alert(‘’‘)}))

)




)
——考新郎( 錯排 ))







