softmax函數–softmax layer

softmax用于多分類過程中，它將多個神經元的輸出，映射到（0,1）區間內，可以看成概率來理解，從而來進行多分類！

假設我們有一個數組$z=(z_1,z_2,...z_m)$,則其softmax函數定義如下：

$$\sigma_i(z)=\frac{exp(z_i)}{\sum_{j=1}^mexp(z_j)} ,i=1,2..,m$$
也就是softmax是個函數映射，將 $z=(z_1,z_2,...z_m)$映射到 $(\sigma_1,\sigma_2,...\sigma_m)$.
其中， $\sum\sigma_i=1.$

如下圖，可以更清楚地表明。

在logistic回歸中，假設$z_i=w_i^Tx+b_i$是第i個類別的線性預測結果，帶入softmax中就可以得到$o_i=\sigma_i(z)$可以解釋成觀察得到的數據x屬于類別i的概率，或者稱為似然（Likehood）。

logistic regression

Logistic Regression 的目標函數是根據最大似然原則來建立的，假設數據x所對應的類別為 y，則根據x我們剛才的計算最大似然就是要最大化$o_y$的值

通常是使用 negative log-likelihood 而不是likelihood，也就是說最小化$-log(o_y)$的值，這兩者結果在數學上是等價的。即$min -log(o_y)<=> max~o_y$

后面這個操作就是 caffe 文檔里說的 Multinomial Logistic Loss，具體寫出來是這個樣子：

$$l(y,o)=-log(o_y)$$
從上面可以看出，計算似然損失，其實是和label一起的。這也是情理之中的，既然我們知道label是某一個，自然我們我希望對應的預測概率盡可能大一點。這就歸結于上面的log損失。

softmax logistic loss

softmax logistic loss就是將softmax與上述的log損失結合到一起，只要把$o_y$的定義展開即可。

$$\hat{l}(y,z)=-log(\frac{e^{z_y}}{\sum_{j=1}^{m}e^{z_j}})$$
其實label(這里指y)的作用就是指定了softmax的序號，也就是告訴是哪一些最小化。

反向傳播

反向傳播，要求根據loss更新weights,需要計算loss對于weight的偏導數。
我們參考了網上的一個例子,來簡單介紹一下如何計算偏導。

$$a_4=\frac{e^{z4}}{e^{z4}+e^{z5}+e^{z6}}， a_5=\frac{e^{z5}}{e^{z4}+e^{z5}+e^{z6}}， a_6=\frac{e^{z6}}{e^{z4}+e^{z5}+e^{z6}}$$
好了，我們的重頭戲來了，怎么根據求梯度，然后利用梯度下降方法更新梯度！

要使用梯度下降，肯定需要一個損失函數，這里我們使用交叉熵作為我們的損失函數，為什么使用交叉熵損失函數，不是這篇文章重點，后面有時間會單獨寫一下為什么要用到交叉熵函數（這里我們默認選取它作為損失函數）
交叉熵函數形式如下：

其中y代表我們的真實值，a代表我們softmax求出的值。i代表的是輸出結點的標號！在上面例子，i就可以取值為4,5,6三個結點（當然我這里只是為了簡單，真實應用中可能有很多結點）

現在看起來是不是感覺復雜了，居然還有累和，然后還要求導，每一個a都是softmax之后的形式！

但是實際上不是這樣的，我們往往在真實中，如果只預測一個結果，那么在目標中只有一個結點的值為1，比如我認為在該狀態下，我想要輸出的是第四個動作（第四個結點）,那么訓練數據的輸出就是a4 = 1,a5=0,a6=0，哎呀，這太好了，除了一個為1，其它都是0，那么所謂的求和符合，就是一個幌子，我可以去掉啦！
交叉熵函數形式如下：

這就回到了我們的softmax logistic loss，其實發現交叉熵損失與softmax logistic loss在輸出只有一個類的時候等價。

參數的形式在該例子中，總共分為w41,w42,w43,w51,w52,w53,w61,w62,w63.這些，那么比如我要求出w41,w42,w43的偏導，就需要將Loss函數求偏導傳到結點4，然后再利用鏈式法則繼續求導即可，舉個例子此時求w41的偏導為:

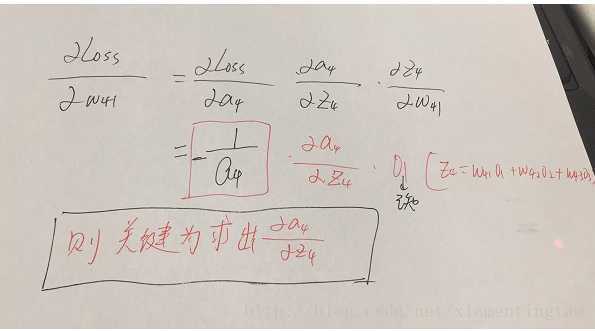
w51…..w63等參數的偏導同理可以求出，那么我們的關鍵就在于Loss函數對于結點4,5,6的偏導怎么求，如下：

這里分為倆種情況：

j=i對應例子里就是如下圖所示：

比如我選定了j為4，那么就是說我現在求導傳到4結點這！

這里對應我的例子圖如下，我這時對的是j不等于i，往前傳：

參考文獻

• Softmax vs. Softmax-Loss: Numerical Stability
• Caffe中Loss Layer原理的簡單梳理
• Softmax 函數的特點和作用是什么？