【隨機森林】random forests 簡單介紹

Random Forest，顧名思義 Random 就是隨機抽取； Forest 就是說這里不止一棵樹，而由一群決策樹組成的一片森林，連起來就是用隨機抽取的方法訓練出一群決策樹來完成分類任務。
RF用了兩次隨機抽取, 一次是對訓練樣本的隨機抽取; 另一次是對變量 (特征) 的隨機抽取。這主要是為了解決樣本數量有限的問題
RF的核心是由弱變強思想的運用。每棵決策樹由于只用了部分變量、部分樣本訓練而成, 可能單個的分類準確率并不是很高。但是當一群這樣的決策樹組合起來分別對輸入數據作出判斷時, 可以帶來較高的準確率。有點類似于俗語三個?皮匠頂個諸葛亮。
隨機森林有兩個重要參數：樹節點預選的變量個數；隨機森林中樹的個數

隨機森林思想來源

$PAC?→Bootstrap?→Bagging?→Random?Forest?←CART?\text { PAC } \rightarrow \text { Bootstrap } \rightarrow \text { Bagging } \rightarrow \text { Random Forest } \leftarrow \text { CART }$

PAC(Probably Approximately Correct)

在該模型中, 若存在一個多項式級的學習算法來識別一組概念, 并且識別正確率很高, 那么這組概念是強學習算法; 而如果學習算法識別一組概念的正確率僅比隨機猜測略好, 那么這組概念是弱學習算法。
如果可以將弱學習算法提升成強學習算法, 那么我們就只要找到一個弱學習算法, 然后把它提升成強學習算法, 而不必去找通常情況下很難獲得的強學習算法。

Bootstrap

根據PAC由弱得到強的思想, 統計學著名學者Bradley Efron在 1979年提出了Bootstraps算法, 這個名字來自于成語 “pull up by your own bootstraps”, 意思是依靠自己的資源, 稱為自助法。
它的思想就是當樣本數量不大, 分布情況未知時, 可以從原始樣本中隨機抽取的多個樣本情況 (弱學習) 來估計原樣本真實的分布情況。它是非參數統計中一種重要的估計統計量方差進而進行區間估計的統計方法。
其基本步驟如下:
– (1) 從原始數據集中, 有放回地抽樣一定數量的樣本
– (2)根據抽出的樣本計算給定的統計量 $T\mathrm{T}$
– (3)重復上述N次 (一般大于1000), 得到 $N$ 個統計量 $T\mathrm{T}$
– (4)計算上述 $N\mathrm{N}$ 個統計量 $T\mathrm{T}$ 的樣本方差, 得到統計量的方差
0.632自助法
假設給定的數據集包含 $d\mathrm{d}$ 個樣本。該數據集有放回地抽樣 $d\mathrm{d}$ 次, 產生 $d\mathrm{d}$ 個樣本的訓練集。原數據中的某些樣本很可能在該樣本集中出現多次。顯然每個樣本被選中的概率是 $\mathrm{d}$ ，因此未被選中的概率就是 $(1 ? 1/ d)$ ，這樣一個樣本在訓練集中沒出現的概率就是 $d\mathrm{d}$ 次都未被選中的概率, 即 $1-1/d) ^d$ 。當 $d$ 趨于無窮大時, 這一概率就將趨近于 $e^{-1}=0.368$ ，所以留在訓練集中的樣本大概就占原來數據集的 $\%$ 。

Bagging

Bagging 又叫bootstrap aggregation, 是Breiman在1993 年提出的方法, 第一步就是根據Bootstrap進行抽樣。
基本的步驟:
– (1)從樣本集中用Bootstrap采樣選出 $n\mathrm{n}$ 個樣本
– (2)在所有屬性上, 對這 $n\mathrm{n}$ 個樣本建立分類器 (CART or SVM or …)
– (3)重復以上兩步m次, i.e. 建立 $m$ 個分類器 (CART or SVM or … )
– (4)將數據放在這m個分類器上跑, 最后vote看到底分到哪一類
這種方法可以大大降低每個分類器的不穩定性, 從而帶來較高的預測準確率。從這個方法再往下發展就是隨機森林了

隨機森林

隨機森林是以決策樹為基本分類器的一個集成學習模型, 它包含多個由Bagging集成學習技術訓練得到的決策樹。
Random Forests不同的是: 在Bagging的基礎上, 使用一種改進的樹學習算法, 在每個候選分裂的學習過程中, 選擇特征值的一個隨機子集。有時被稱為 “feature bagging”。
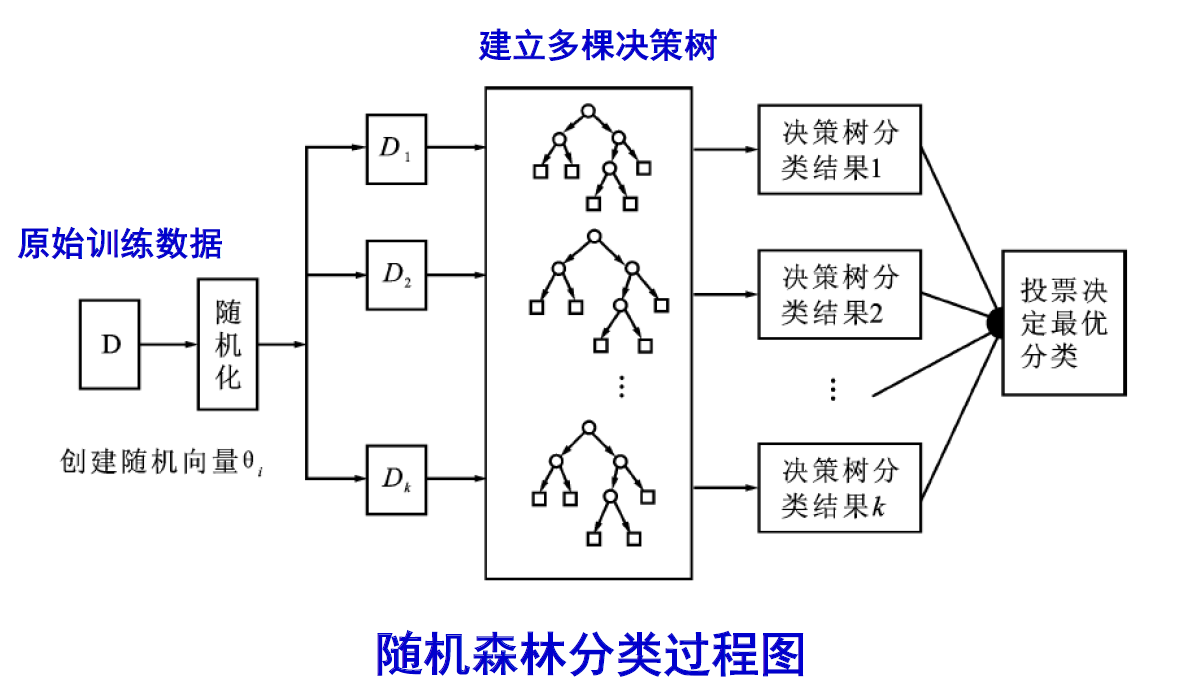
該算法用隨機的方式建立起一棵棵決策樹, 然后由這些決策樹組成一個森林, 其中每棵決策樹之間沒有關聯, 當有一個新的樣本輸入時, 就讓每棵樹獨立的做出判斷, 按照多數原則決定該樣本的分類結果。

構建隨機森林

(1) 從樣本集中用bagging采樣選出 $n\mathrm{n}$ 個樣本, 預建立CART
(2) 在樹的每個節點上, 從所有屬性中隨機選擇 $k\mathrm{k}$ 個屬性, 選擇出一個最佳分割屬性作為節點（RI 和 RC ）
(3) 重復以上兩步m次, i.e. 構建m棵CART (不剪枝)
(4) 這 $m\mathrm{m}$ 個CART形成Random Forest

利用隨機森林預測

(1) 向建立好的隨機森林中輸入一個新樣本
(2) 隨機森林中的每棵決策樹都獨立的做出判斷
(3) 將得到票數最多的分類結果作為該樣本最終的類別

影響性能的因素

森林中單棵樹的分類強度（Strength）：每棵樹的分類強度越大, 則隨機森林的分類性能越好
森林中樹之間的相關度（Correlation）：樹之間的相關度越大,則隨機森林的分類性能越差。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/258274.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/258274.shtml
英文地址，請注明出處：http://en.pswp.cn/news/258274.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！