目錄
?
4.1 多元函數的泰勒展開
4.2方向導數與梯度
4.2.1方向導數
n元函數在點沿特定方向的方向導數
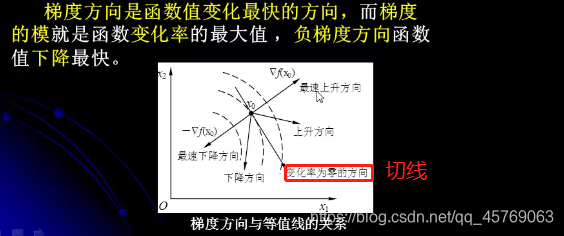
4.2.2梯度
4.3二次函數及正定矩陣
4.4凸函數與凸規劃
4.4.1凸函數
4.4.2凸規劃
4.4無約束優化問題的極值條件
4.5約束優化問題的極值條件(重點考點)
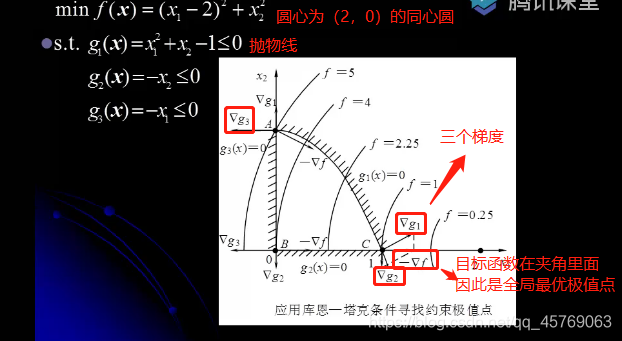
例:考點重點(判斷一個點是否為這規化的最優極值點)
因為目標函數和約束函數都凸函數,而點(1,0)又符合K-T條件,因此該點是全局最優約束極值點
4.1 多元函數的泰勒展開


求解海森矩陣:
例1:
?
例2:



?
4.2方向導數與梯度
4.2.1方向導數



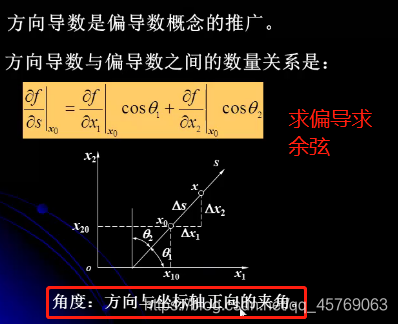
n元函數在點沿特定方向的方向導數


4.2.2梯度












4.3二次函數及正定矩陣








4.4凸函數與凸規劃
4.4.1凸函數

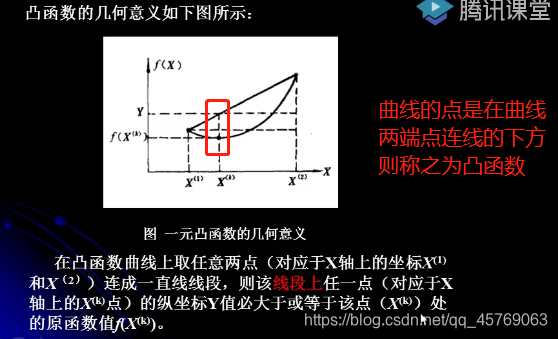

4.4.2凸規劃


4.4無約束優化問題的極值條件



海森矩陣怎么求解
4.5約束優化問題的極值條件(重點考點)





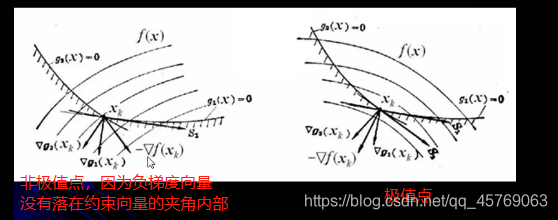

例:考點重點(判斷一個點是否為這規化的最優極值點)
求解步驟:
1.判斷所給點是否為可行點,即看是否滿足約束條件
2.從約束條件中找到起作用的約束條件,即約束條件等于0
3.求出目標函數與起作用的約束函數的梯度
4.將梯度帶入等式條件中列出等式,算出拉格朗日乘子
5.若拉格朗日因子是非負非零則是極值點
6.判斷是否為全局最優極值點:目標函數和起作用的約束函數是凸函數,且所給點滿足K-T條件,則為全局最優極值點
?








)









)


)
