目錄
一、相關概念
1、iou
1)理論計算
2)Python代碼(代碼參考yolov3模型util.py文件)
2、nms
1)基本思路
2)標準nms和soft-nms
3)Python代碼實現(yolov3中util.py文件,增加了注釋)
4)標準nms的缺點
一、相關概念
1、iou
1)理論計算
參考:https://blog.csdn.net/zouxiaolv/article/details/107400193
 ????????????????????????
????????????????????????
物體檢測需要定位出物體的bounding box,就像上面的圖片一樣,我們不僅要定位出車輛的bounding box 我們還要識別出bounding box 里面的物體就是車輛。
對于bounding box的定位精度,有一個很重要的概念,那就是定位精度評價公式:IOU。

IOU表示了bounding box 與 ground truth 的重疊度,如下圖所示:
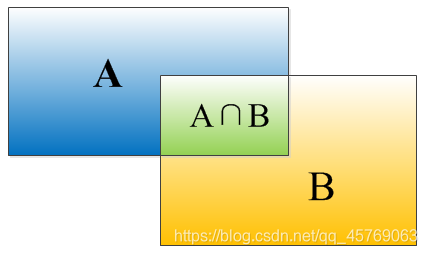
這里寫圖片描述
矩形框A、B的一個重合度IOU計算公式為:
???????????????????????????????????????????????????????????????? IOU=Area(A∩B)/Area(A∪B)
就是矩形框A、B的重疊面積占A、B并集的面積比例:
???????????????????????????????????????????????????????????????? IOU=SI/(SA+SB-SI)
如何計算IOU(交并比)
??????? ??????????????????????? ?
??????????????????????? ?
首先求出重合面積:
???? 選取兩個矩形框左頂角的橫,縱坐標的最大值,x21,y21;選取兩個矩形框右下邊角的橫縱坐標的最小值,x12,y12;
重合面積計算:
???????????????????????????? inter=??? | x12-x21 *| y12-y21 |
并集的面積計算:
?????????????????????????????? b = | x12-x21? |*| y12-y21 |+ | x21-x22 || y21-y22? | - inter
計算IOU:
?????????????????????????????????? IOU=inter/b
2)Python代碼(代碼參考yolov3模型util.py文件)
def bboxes_iou(boxes1, boxes2):'''兩個都是數組,注意兩個box的維度必須一致,一般是二維box:[[xmin,ymin,xmax,ymax],[xmin,ymin,xmax,ymax],...]'''boxes1 = np.array(boxes1)# (1,4)boxes2 = np.array(boxes2) # (n,4)# 計算兩個box的面積boxes1_area = (boxes1[..., 2] - boxes1[..., 0]) * (boxes1[..., 3] - boxes1[..., 1]) # (1,1)boxes2_area = (boxes2[..., 2] - boxes2[..., 0]) * (boxes2[..., 3] - boxes2[..., 1]) # (n,1)left_up = np.maximum(boxes1[..., :2], boxes2[..., :2])right_down = np.minimum(boxes1[..., 2:], boxes2[..., 2:])inter_section = np.maximum(right_down - left_up, 0.0)inter_area = inter_section[..., 0] * inter_section[..., 1] # 重疊區域union_area = boxes1_area + boxes2_area - inter_area # 全部面積ious = np.maximum(1.0 * inter_area / union_area, np.finfo(np.float32).eps) # iousreturn ious2、nms
非極大值抑制(Non-Maximum Suppression,NMS),顧名思義就是抑制不是極大值的元素,用于目標檢測中,就是提取置信度高的目標檢測框,而抑制置信度低的誤檢框。一般來說,用在當解析模型輸出到目標框時,目標框會非常多,具體數量由anchor數量決定,其中有很多重復的框定位到同一個目標,nms用來去除這些重復的框,獲得真正的目標框。如下圖所示,人、馬、車上有很多框,通過nms,得到唯一的檢測框。

1)基本思路
所謂非極大值抑制:先假設有6個矩形框,根據分類器類別分類概率做排序,從小到大分別屬于車輛的概率分別為A<B<C<D<E<F。
(1) 從最大概率矩形框F開始,分別判斷A、B、C、D、E與F的重疊度IOU是否大于某個設定的閾值;
(2) 假設B、D與F的重疊度超過閾值,那么就扔掉B、D;并標記第一個矩形框F,是我們保留下來的。
(3) 從剩下的矩形框A、C、E中,選擇概率最大的E,然后判斷A、C與E的重疊度,重疊度大于一定的閾值,那么就扔掉;并標記E是我們保留下來的第二個矩形框。
(4) 重復這個過程,找到所有被保留下來的矩形框。
2)標準nms和soft-nms
參考:https://zhuanlan.zhihu.com/p/89426063

bi為待處理BBox框,B為待處理BBox框集合,si是bi框更新得分,Nt是NMS的閾值,D集合用來放最終的BBox,f是置信度得分的重置函數。 bi和M的IOU越大,bi的得分si就下降的越厲害。
經典的NMS算法將IOU大于閾值的窗口的得分全部置為0,可表述如下:
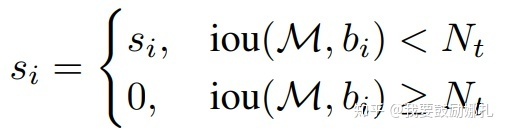
這種是加權線性的

具體其他的可以參考:https://zhuanlan.zhihu.com/p/89426063
3)Python代碼實現(yolov3中util.py文件,增加了注釋)
def nms(bboxes, iou_threshold, sigma=0.3, method='nms'):""":param bboxes: (xmin, ymin, xmax, ymax, score, class),是一個數組,關于(n,6),n是檢測出的box個數Note: soft-nms, https://arxiv.org/pdf/1704.04503.pdfhttps://github.com/bharatsingh430/soft-nms"""classes_in_img = list(set(bboxes[:, 5])) # 得到不同類別標簽的列表,如[0,1,2],標簽號best_bboxes = [] # 存放最好的boxfor cls in classes_in_img: # 遍歷類別號列表cls_mask = (bboxes[:, 5] == cls) # 這里返回的是一個True or False的掩模列表,True則表示bboxes中對應索引號的box是屬于這個類cls_bboxes = bboxes[cls_mask] # 根據掩模獲得屬于那一類的box,依舊是二維數組while len(cls_bboxes) > 0: # 這里一直在循環,直到box列表為空max_ind = np.argmax(cls_bboxes[:, 4]) # 獲得這類得分最高的box索引best_bbox = cls_bboxes[max_ind] # 將分數最高的box作為最佳boxbest_bboxes.append(best_bbox) # 添加# 從box列表中去除最佳boxcls_bboxes = np.concatenate([cls_bboxes[: max_ind], cls_bboxes[max_ind + 1:]])# 計算得到兩個box之間的iou(重疊部分除以一起共同的面積),下面這里其實進行了批量操作,將最佳box和剩下的box進行了計算# np.newaxies,表示增加一個維度iou = bboxes_iou(best_bbox[np.newaxis, :4], cls_bboxes[:, :4])weight = np.ones((len(iou),), dtype=np.float32) # 置信度,當iou大于0.7,說明重疊的部分很大,可以視為一個框,故丟棄assert method in ['nms', 'soft-nms']if method == 'nms': # 標準nmsiou_mask = (iou > iou_threshold) # 得到一個掩模,iou大于設定閾值的設置為TRUEweight[iou_mask] = 0.0 #大于閾值的box的置信度置為0if method == 'soft-nms': # soft-nms,不直接丟棄大于閾值的boxweight = np.exp(-(1.0 * iou ** 2 / sigma)) # sigma為懲罰因子,這個越小,置信度越小,越容易被拋棄cls_bboxes[:, 4] = cls_bboxes[:, 4] * weight # 這里是將剩下的box的得分乘以了iou置信度,與bestbox重疊的丟棄了score_mask = cls_bboxes[:, 4] > 0. # 取大于0的也就是丟棄了重疊的,這也是掩模cls_bboxes = cls_bboxes[score_mask] # 根據掩模跟新剩下的box,進行下一輪的nmsreturn best_bboxes
4)標準nms的缺點
1、NMS算法中的最大問題就是它將相鄰檢測框的分數均強制歸零(即將重疊部分大于重疊閾值Nt的檢測框移除)。在這種情況下,如果一個真實物體在重疊區域出現,則將導致對該物體的檢測失敗并降低了算法的平均檢測率。
2、NMS的閾值也不太容易確定,設置過小會出現誤刪,設置過高又容易增大誤檢。
3、NMS一般只能使用CPU計算,無法使用GPU計算。
?



修改學習率(定值+自適應))



)



)


)




