L~M方法：

首先，L~M方法首先是一種非線性規劃方法；其次其主要用于無約束的多維非線性規劃問題；最后，它是一階牛頓法的一種改進，改進的目的是為了更快的收斂。

既然如此，那么讓我們先來了解一下L~M方法的“前輩”一階牛頓法吧。對一階牛頓法的理解會幫助我們了解L~M方法的總體思路。

???????? 對于無約束的多維非線性規劃問題，起碼我們需要一個可以令人接受的參數估計的初始解，我們設其為：X^k。（舉個例子，這就是張正友標定法中通過純粹的幾何推導得出的攝像機參數）。在X^k的基礎上，我們去尋找比X^k更“靠譜”的估計值。既然我們已經認為X_k可以令人接受，那么更好更精確的估計值應該在X_k的附近，在距離X_k長度為Δ^k的地方。那么，現在我們用一點點高等數學的知識：泰勒展開式。對于一階牛頓法，我們用一階泰勒展式逼近X^k附近點的f(X_k+Δ^k)估計值。（這里提到的量都是矩陣形式哦比如，在張正友標定法中f(X_k+Δ^k)由u和v組成）如下

? ? ? ? 假設ε=X^k+1-X^k在某時以變化的緩慢到我們認為算法以收斂。我們稱ε為終止條件。

? ? ? ? 那么，我們就這樣迭代下去，總會得到符合我們預期的X^k+1。

? ? ? ? 以上就是一階牛頓法，說白了就是一個不斷向著有利方向迭代的過程。

? ? ? ? L~M方法是在一階牛頓法基礎上的改進。為加快收斂，L~M把上面的正規化方程改成了增量正規化方程。如下：

? ? ? ? ?λ就是增量方程中所謂的增量。

? ? ? ? ?L~M方法中，取增量的規則如下：

? ? ? ? ?最初，設λ=0.0001，如果增量方程的解Δ^k導致e^k減小，我們就接受這個λ，并在下一次迭代中使用λ/10代換λ。如果λ值對應的增量方程的解Δ^k導致e^k增大，我們就舍棄這個λ，并將其代換為10λ重解增量方程。循環往復直到e^k下降為止。λ^k+1=10λ^k

? ? ? ? ?L~M也是迭代循環，直到總會得到符合我們預期的X^k+1為止。

? ? ? ? 以上就是L~M方法的原理與出處。大家一定覺得昏昏欲睡了。那么下一部分，應該是大家喜聞樂見的。玉米，將L~M算法的過程總結成算法流程圖，與大家分享。||Δ^k||<ε

二、L~M這樣用：

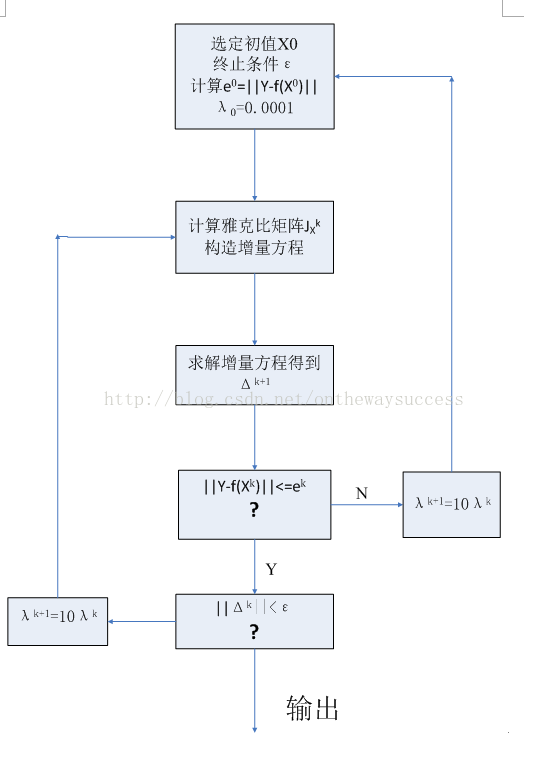
? ? ? ? ?該流程圖就是L-M算法的算法流程。玉米就不多說什么了，流程圖更清晰一些。

?

? ? ? ? 玉米才疏學淺，文章中如有紕漏，請大家批評指正！