Bzoj1051 受歡迎的牛

每一頭牛的愿望就是變成一頭最受歡迎的牛。現在有 N 頭牛，給你 M 對整數 (A,B)，表示牛 A 認為牛 B 受歡迎。這種關系是具有傳遞性的，如果 A 認為 B 受歡迎，B 認為 C 受歡迎，那么牛 A 也認為牛 C 受歡迎。你的任務是求出有多少頭牛被除自己之外的所有牛認為是受歡迎的

---

第一眼是個很弱智的Tarjan縮點，然后判斷有沒有連通分量的入度為連通分量個數減一

但是我把傳遞性想的太簡單了

如果有下圖這樣的，我就只會判定出3號點有一個入度，但是正確值為2

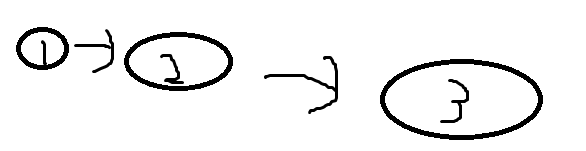
所以我們換一個角度，從縮點的性質來考慮

我們知道，縮點之后的圖是一個DAG（有向無環圖）

所以一個節點如果有出度，就不可能被它所到的點崇拜，否則就有環了

所以我們得出了第一條結論，只有出度為零的點才能被所有點崇拜

然后有的人會問如果有多個節點的出度為零怎么辦呢

即使不從圖的角度來看，這兩個出度為零的點也是不可能互相崇拜的，所以不成立

下面給出代碼：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cmath>
using namespace std;
inline int rd(){int x=0,f=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';return x*f;
}
inline void write(int x){if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10+'0');return ;
}
int n,m;
int head[1000006],nxt[1000006],to[1000006];
int total;
void add(int x,int y){total++;to[total]=y;nxt[total]=head[x];head[x]=total;return ;
}
int dfn[1000006];
int low[1000006];
int tot=0;
int book[1000006];
int sta[1000006];
int set=0;
int v[1000006];
int cnt=0;
int color[1000006];
void tarjan(int x){low[x]=dfn[x]=++tot;sta[++set]=x;book[x]=1;for(int e=head[x];e;e=nxt[e]){if(!dfn[to[e]]){tarjan(to[e]);low[x]=min(low[x],low[to[e]]);}else if(book[to[e]]) low[x]=min(low[x],dfn[to[e]]);}if(dfn[x]==low[x]){cnt++;book[x]=0;v[cnt]++;color[x]=cnt;while(set&&sta[set]!=x){book[sta[set]]=0;v[cnt]++;color[sta[set]]=cnt;set--;}set--;}return ;
}
int du[1000006];
int main(){n=rd(),m=rd();for(int i=1;i<=m;i++){int x=rd(),y=rd();add(x,y);}for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);int ans=0;for(int i=1;i<=n;i++){for(int e=head[i];e;e=nxt[e]){if(color[i]!=color[to[e]]){du[color[i]]++;}}}int num=0;for(int i=1;i<=cnt;i++){if(du[i]==0){num++;ans+=v[i];}}if(num==1) write(ans);else write(0);return 0;
}

?